阶梯形圆角对曲轴应力优化作用的研究

朱晨虹　兰　箭

(武汉理工大学现代汽车零部件技术湖北省重点实验室　武汉　430070)

阶梯形圆角对曲轴应力优化作用的研究

朱晨虹兰箭

(武汉理工大学现代汽车零部件技术湖北省重点实验室武汉430070)

摘要：利用ANSYS对某型号V型12缸柴油发动机的曲轴进行整轴的有限元分析，研究其在所有选定危险工况下的应力大小、应力分布，以及变形情况.对各工况下最大应力的大小、分布位置进行总结和讨论，并对曲轴存在的危险性进行预测.为了优化曲轴结构强度，提出了利用阶梯形圆角结构对该曲轴进行圆角应力优化，通过对比其与普通圆角结构对应力的影响，发现圆角参数取中间值时，整轴应力峰值最小，与普通圆角比降低45 MPa，且对应力分布也有一定改善作用，证明这种圆角可以得到较明显的优化圆角应力的作用.

关键词：曲轴；圆角应力；优化；有限元

朱晨虹(1989- )：女，硕士生，主要研究领域为汽车零部件CAE

0引言

曲轴作为发动机的核心部件，是发动机能否正常运转的关键.某型号的柴油机曲轴经常出现裂纹甚至断裂的现象而导致整轴报废.通过试验探测裂纹位置，发现该曲轴各连杆轴颈和主轴颈圆角的位置裂纹居多.因此，从优化圆角结构入手对曲轴应力进行改进是一个比较合理的选择.曲轴圆角结构多应用普通圆角、沉割槽圆角和阶梯形圆角结构[1].目前对前2种圆角的研究较多，基于此事实，着重研究该柴油机曲轴在改进为阶梯形圆角的情况下的应力及其分布.

1模型

利用UG建立曲轴三维模型.多数研究为了方便计算而采用单拐模型[2-3]，虽然有研究证明单拐模型与整轴模型的应力大小结果相近，但是单拐模型无法显示在所有危险工况下应力分布位置的规律，进而无法对危险位置进行预测.因此，应采用整轴模型进行分析.

利用ANSYS进行有限元分析.为了方便计算，模型必须进行简化处理才能用于有限元分析,为了得到较精确的应力分布结果，不忽略油孔结构，只是去除螺栓孔等对应力产生影响更小的结构.该曲轴材料为42CrMoA，其弹性模量为206MPa，泊松比0.3，密度为7.82kg/m3.

有限元网格划分采用带中间节点的四面体单元.采用自由网格划分，划分精度为8，基本尺寸为0.02.自由网格划分的好处在于它可以比较智能的将圆角和油孔的位置细化，优化了网格的分布.见图1.

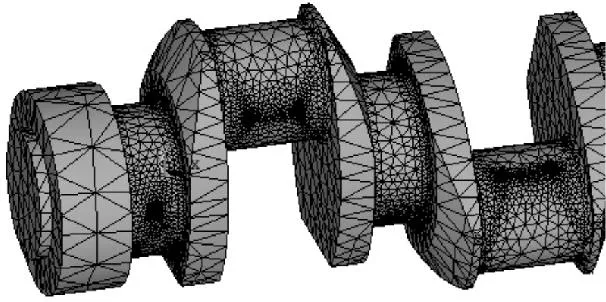
图1　网格分布局部图

2危险工况确定

与所要研究的曲轴相匹配的发动机是一个四冲程60°夹角V型12缸的柴油发动机.从输出端看，令左边一排气缸编号为A1～A6，右边为B1～B6.已知该发动机的点火顺序为A1 -B2 -A5 -B4 -A3 -B1 -A6-B5 -A2 -B3 -A4 -B6.根据曲轴发火规律制定发动机工作循环表，可以发现，每当有一个气缸开始做功时，另外也有2个缸也在做功行程中.

对该曲轴做静力学分析时，主要考虑危险时刻受载荷的影响.根据发动机动力学分析，气缸最高爆发压力与活塞行程成反比关系，在曲轴转角为0°时，即活塞位于上止点位置，气缸爆发压力达到最高值[4].此时作用在连杆轴颈上的力远高于其他作用力.为了方便力学分析，忽略了点火提前角.选取每个缸开始做功时刻为最危险时刻，12个气缸即共有12个危险工况.

3边界条件

3.1力边界条件

曲轴在工作过程中受力十分复杂，包括自身重力，自身旋转质量惯性力、平衡重作用的旋转质量惯性力、连杆力，以及输出端的反作用转矩这5种力.很多力大小和方向呈周期性变化.将经典的曲柄连杆机构的受力情况(见图2a))联想到所要研究的曲轴上，分析在做功行程中的连杆对曲轴的力的作用见图2b)[5].

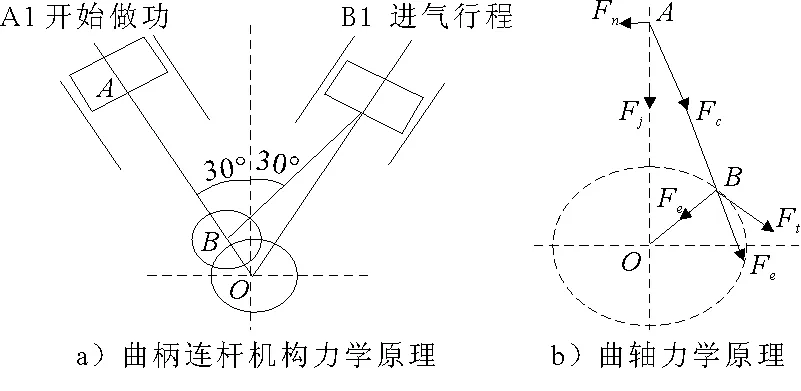
图2　曲轴受力原理

3.1.1重力以及旋转质量惯性力重力以重力加速度的方式加载；自身旋转惯性力通过给定转速和材料密度实现.另外，平衡重旋转惯性力的作用不可忽略.本文通过其密度体积和结构大约估算其作用力，最后以面载荷形式加到曲柄端面上.

3.1.2连杆力在曲轴所承受的所有载荷中，连杆力最为关键，其大小直接影响最大应力.在所有的12个连杆中，只计入处在做功行程的气缸所产生的连杆力，即每一工况有3个不同连杆表面受连杆力.

采用面载荷的形式加载连杆力.根据传统的理论,以及有限宽度轴颈油膜应力分布规律，且忽略油孔产生的压力峰值突变的影响，面载荷的分布形式应为：载荷q沿连杆轴颈按二次抛物线规律分布；沿轴颈圆周方向120°范围内按余弦规律分布.

(1)

式中:Fc为连杆力；L为1/2轴颈长度；R为曲柄半径；x为轴向坐标；θ为作用角度.

ANSYS会将力以函数面压力的形式加载到轴颈面上，最终作用于每一个节点上.

3.1.3输出端反转矩在曲轴旋转过程中，输出端不可避免的会受到来自飞轮等结构的反转矩作用力，在文献[6]等文献中，多数忽略这个力的作用.本文在对比有输出端转矩和无输出端转矩的两种曲轴受力结果后，发现端部转矩作用力虽然很小，但是会影响应力的峰值，因此转矩的作用仍不可忽略.

(2)

式中:Pe为额定功率；n为发动机转速.

ANSYS通过在旋转轴线上建立一个质量单元，绑定其与端面上所有节点，最终通过对该点施加转矩将力矩均匀的加载到端面上.

3.2位移边界条件

一方面模拟输出端止推轴承作用，即约束靠近旋转中心的几个点在轴向上的位移为0[7]；另一方面模拟主轴颈支撑方式，每一主轴颈所受的力的大小和作用面都同时受到相邻两边气缸的影响.由于计算的复杂性，为减少工作量，用弹簧单元来近似模拟主轴颈弹性支撑，在主轴颈外定义节点并与主轴颈上的节点连接作为弹簧模拟轴承在该方向的支撑，弹簧单元刚度取1.98×1011N/m，接近轴承实际刚度.由于变负荷轴承工作时轴颈与轴承接触位置随轴承负荷的不同而变化.因此弹簧支撑的作用面取在和该工况下连杆力作用方向相对的主轴颈面上的120°范围内.

4应力结果

对曲轴在12个危险工况下的应力进行有限元分析，采用完全相同的模型、材料参数，网格精度等，以利于对结果进行总结和对比.首先以工况1应力结果为例进行分析，再对12个危险工况下的应力结果进行总结讨论.

4.1曲轴在工况1下应力结果及分析

1) 应力情况应力分布主要表现为各连杆轴颈圆角处应力偏大,各主轴颈圆角处应力偏大,连杆力作用的轴颈表面局部应力偏大,油孔位置并没有出现局部明显的应力集中.最大应力为131MPa，位置在与做功位置连杆轴颈相连的第二主轴颈圆角处，见图3a).

图3　有限元结果局部图

2) 变形情况由总体应力分布云图4可见，曲轴明显主要产生了弯曲变形，最大变形为1.83×10-4m，出现在自由端.由结构转动结果图3b)可以看出扭转主要集中出现在输出端部附近，且产生的应力远小于整体的应力值.说明曲轴产生的变形主要是弯曲变形和微小的轴向窜动，受扭转的作用较小.

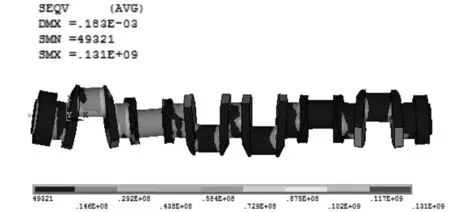
图4　曲轴整轴模型应力分布图

4.2曲轴在12个工况下应力结果及分析

曲轴在12个危险工况下的应力结果总结于图5和表1中，可以看出：

1) 应力大小由表1可以看出，曲轴在12工况下的最大应力都处在101～159MPa范围内，其结果都小于极限值.最高值出现在工况6，即B1缸开始做功的时刻，可认为工况6为较危险的工况.

表1　普通圆角的曲轴在各危险工况下的最大应力σmax

2) 应力分布选用最大应力出现的点为最危险点，将它们标于曲轴简图5中.由图5可见，曲轴在11个工况下的危险点都出现在主轴颈圆角位置，只有工况5出现在连杆轴颈圆角[8-9].另外，最大应力分布位置并不均匀，多出现在1，2，3主轴颈处，即靠近输出端的位置.图5中粗体数字代表这些工况下的最大应力具有相同的轴向坐标值，即出现在在同一曲轴截面上.

图5　曲轴简图及十二危险工况下的应力分布图1

3) 可断定主轴颈圆角为曲轴最易发生裂纹的位置，且越靠近输出端的圆角越危险.且判定此曲轴的1，2，3主轴颈如图5所示位置的发生断裂危险性较大，尤其是2号主轴颈.

因此，曲轴的强度需要改进，且对强度的改进有必要从圆角的优化开始.

5曲轴圆角结构优化

改进圆角结构是优化曲轴应力的一种比较有效的方式[10].文献[1-2]等研究中，曲轴多用普通圆角结构或沉割槽式的结构，见图6a).应力集中往往出现在结构发生突变的位置，阶梯形圆角结构由于阶梯式的结构对轴颈位置的结构突变起到一定的缓和作用.因此，着重研究该曲轴在阶梯形圆角结构(见图6b))下的应力优化.

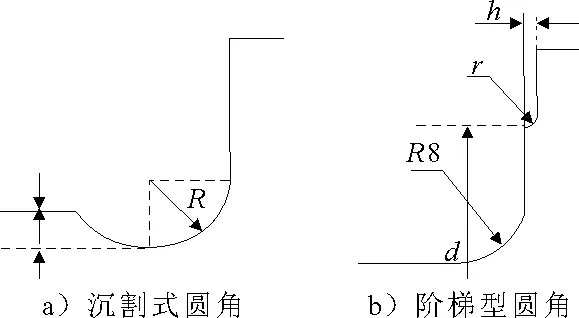
图6　圆角结构和尺寸示意图

5.1不同结构参数在最危险工况6下的应力结果

此阶梯形圆角结构除参数R8外，参数d,h,r都未确定，见图6b).为了研究阶梯形圆角的最优结构参数组合，运用ANSYS专用的APDL语言编程，对曲轴进行了参数化分析.选择最危险的工况6分析.参数大小范围的确定考虑了曲轴轴颈尺寸、机体尺寸，以及两者之间的配合等.参数取值范围：r，2-12mm，h，0～0.8mm，d，201～222mm.当一个参数取不同值时，另两个参数取中间值，即r=8mm，d=210mm，h=0.5mm.共有22组参数.

5.1.1最大应力大小

1) 图7为d-σmax曲线图.由图7可见，当h和r一定时，随着圆角尺寸d增大，最大应力呈现两边高中间低，最低点在d=210mm处，为114MPa.另外，图中A点为d=200mm时的最大应力，即结构仍为普通圆角时.除了当d取201mm时，由于圆角处结构细小而产生局部高应力集中，其他尺寸的应力值都低于普通圆角时的值.

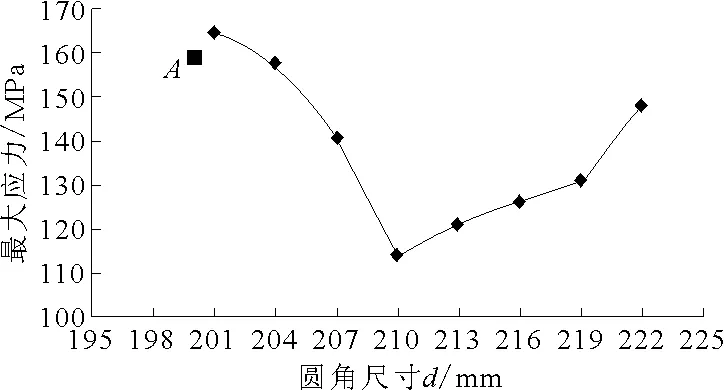
图7　圆角尺寸d与最大应力σmax的关系

2) 图8为h-σmax曲线图.由图8可见，当r和d一定时，随着圆角尺寸h增大，最大应力呈现先降低后升高的趋势，最低点在h为0.5mm处，值为114MPa.另外，图中B点为h=0时，即结构仍为普通圆角时的最大应力，可以看出，无论h取何值，最大应力都明显低于普通圆角结构时的最大应力.

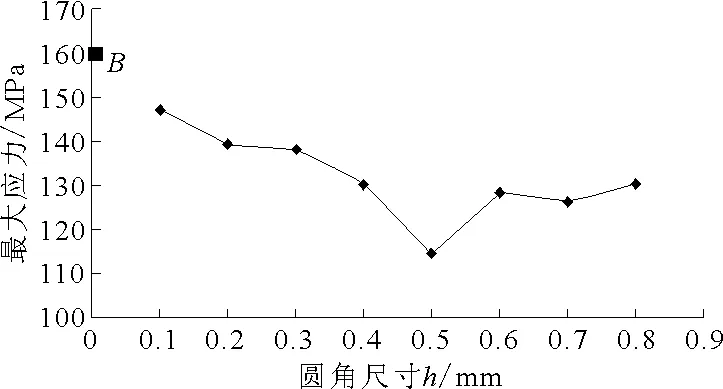
图8　圆角尺寸h与最大应力σmax的关系

3) 图9为r-σmax曲线图.由图9可见，当h和d一定时，随着圆角大小r从2～12mm增大，最大应力呈现两边高中间低的变化，最低点在r=8mm处，为114MPa.

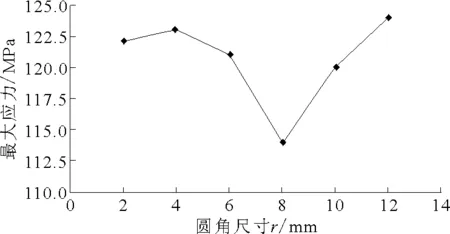
图9　圆角尺寸r与最大应力σmax的关系

通过比较图7～9,可以得出最优的结构组合是R=8mm，h=0.5mm，d=210mm，使得最大应力减小45MPa.也就是这3个参数取值于范围内的中间值的时候.

5.1.2最大应力分布位置

最大应力分布位置与普通圆角结构比，大多处在相同位置.通过比较最大应力点坐标，当d为210，222mm时，最大应力位置发生改变.初步认定这种结构有一定的改进应力分布的作用，但改进作用小.

5.2最优结构参数在12工况下的应力结果

为进一步验证该结构对应力的优化作用，对该圆角结构的曲轴模型进行12个危险工况下的应力分析，总结如下.

1) 应力大小表2为阶梯形圆角的曲轴在各危险工况下的最大应力σmax.由表2可见，曲轴在12个工况下的最大应力在93.6～126MPa之间，最大值出现在工况1，即A1缸开始做功的时刻.最大应力值的范围减小，整体也降低.

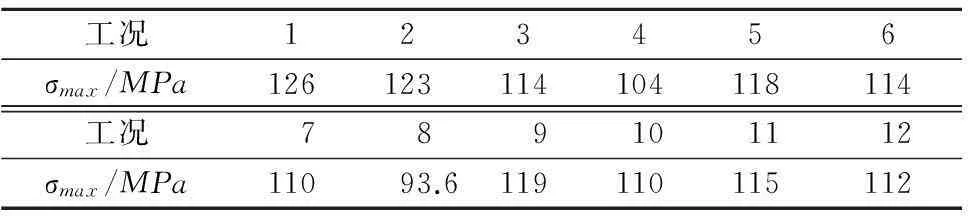
表2　阶梯形圆角的曲轴在各危险工况下的最大应力σmax

2) 应力分布同样取最大应力出现的位置标于曲轴简化图10中，可以看出，曲轴在所有工况下的危险点都出现在主轴颈圆角附近，最大应力分布位置仍不均匀，多出现在1,2,3主轴颈处，即靠近输出端的位置.

图10　曲轴简图及12工况下的应力分布图

5.32种结构的对比

将2种结构下的曲轴在各危险工况下的最大应力呈现于图11，对比得到：(1) 2条曲线变化趋势相似，即不论结构如何改变，曲轴的最大应力规律改变不大； (2) 阶梯形圆角结构的曲线较普通圆角结构的曲线平滑，即曲轴在一个工作循环内的最大应力范围缩小；(3) 阶梯形圆角曲线除工况4最大应力点略高于普通圆角结构的值，其余都位于普通圆角曲线的下方，各工况下最大应力大小有明显的降低；(4) 从简图5和简图10的应力分布情况对比可以看出，阶梯形圆角结构的应力分布情况较普通圆角结构有一定的改变，但是仍呈现输出端应力集中情况明显.

图11　普通圆角结构的曲轴和阶梯形圆角结构的曲轴在各危险工况下的最大应力对比图

6结论

1) 曲轴在工作过程中主要产生弯曲变形，受扭转作用较小，但转矩作用会影响应力峰值；曲轴油孔位置产生的应力集中情况较圆角位置少.

2) 本文研究的曲轴最大应力几乎都出现在主轴颈圆角附近，且远高于其他位置.在研究曲轴应力时主要考虑圆角位置的应力，在研究曲轴强度优化改进时主要从主轴颈圆角入手.

3) 不同于对曲轴进行单拐模型分析，对整轴进行分析不仅可以得到某一危险工况下曲轴上最大应力的值，还能得到最大应力在整轴上的分布规律.

4) 运用ANSYS的APDL语言进行程序编写，对阶梯形圆角的曲轴进行参数化计算，减少了大量的重复操作，得到了较好的结论，即最小应力结果出现在各参数设为其范围内的中间值的时候.

5) 阶梯形圆角结构对曲轴应力的改进起到明显得的作用，其作用主要优化了应力峰值和一个工作周期内的应力峰值波动范围，而对应力峰值分布位置的改进作用较小.故对应力峰值分布改善的研究仍需继续进行.

参 考 文 献

[1]诸葛良，李爱军，王明武.基于三维有限元分析的曲轴圆角优化设计[J].内燃机工程,2002,23(2)：47-51.

[2]李文，廖日东，左正兴,等.高强化柴油机曲轴过渡圆角应力计算的研究[J]. 汽车工程,2013,35(6)：565-572.

[3]俞水良，陈汝珍，徐汉章,等.基于ANSYS的错拐曲轴有限元分析[J]. 内燃机工程,2007,28(2)：65-68.

[4]沈海涛.郑水英. 柴油机曲轴危险工况的确定及其静强度分析[J].机械设计,2006,23(11)：28-31.

[5]迟志伟，宋希庚，薛冬新,等. 基于ANSYS的6110柴油机曲轴有限元分析[J].小型内燃机与摩托车,2009,38(3)：1-4.

[6]FANJiangpeng.FiniteelementanalysisofcrankshaftbyABAQUS[C].2011SecondInternationalConferenceonDigitalManufacturing&Automation,2011：545-548.

[7]刘万选，魏敬乾.16V240Z型内燃机曲轴的强度性能分析[J].机械工程师,2012(12)：64-65.

[8]何芝仙，桂长林，李震,等. 计入轴瓦变形的曲轴动应力和疲劳强度计算[J].机械工程学报,2009,45(11):91-98.

[9]GUYingkui.StrengthanalysisofdieselenginecrankshaftbasedonPRO/EandANSYS[C].2011ThirdInternationalConferenceonMeasuringTechnologyandManufacturingAutomation,2011：362-364.

[10]陈宏，聂志斌，吴亚龙.某型柴油机曲轴圆角优化设计研究[J].内燃机,2012(3)：3-5.

中图法分类号：TK413.3

doi:10.3963/j.issn.2095-3844.2015.01.046

收稿日期：2014-04-11

AStudyontheOptimalEffectofSteppedFilletonCrankshaftStress

ZHUChenhongLANJian

(Hubei Key Laboratory of Advanced Technology of Automotive Components，

Wuhan University of Technology,Wuhan 430070,China)

Abstract：In this study, finite element analysis of a complete crankshaft model working for a “V” version 12 cylinders diesel engine was carried out. The study mainly focuses on the stress distribution and deformation of crankshaft during dangerous working condition. By comparing the peak value and distribution of these stresses, the danger of the structure was predicted. Stepped fillet structure was introduced to optimize the stress of crankshaft. It was proved useful after comparing the stress result of crankshaft with common fillet, undercut fillet and stepped filet.

Key words：crankshaft; fillet stress; fillet optimization; FEM