Serret-Frenet框架下的神经滑模船舶路径跟踪控制

李湘平　吴汉松　阮苗锋

(海军工程大学电气工程学院　武汉　430033)

Serret-Frenet框架下的神经滑模船舶路径跟踪控制

李湘平吴汉松阮苗锋

(海军工程大学电气工程学院武汉430033)

摘要：针对欠驱动船舶在恒定速度航行下的路径跟踪问题，提出了一种在Serret-Frenet框架下，基于输入输出线性化的神经滑模控制算法.该算法利用Serret-Frenet框架下船舶运动方程的推导形式，将其转换为类似于直线航迹控制的问题，采用神经网络对基于趋近律的滑模控制进行优化，解决了趋近律滑模控制对系统模型的依赖性，提高了控制器的鲁棒性，并设计了状态观测器对控制对象状态进行重构，以解决系统状态量测量误差对控制效果的影响.在无干扰和存在干扰及参数摄动的条件下分别进行了仿真，结果表明该控制律具有良好的跟踪性能.

关键词：欠驱动船舶；路径跟踪；输入输出线性化；神经滑模控制

李湘平(1990- )：男，硕士生，主要研究领域为船舶非线性控制

0引言

研究欠驱动船舶的路径跟踪控制，可以简化控制系统的结构、降低成本.目前就欠驱动船舶的路径跟踪问题，已经有了大量的研究[1-6].文献[1-3]给出了自适应的航迹控制算法，但不适合曲线航迹控制的情况；文献[4]采用反步法的滑模控制实现了曲线航迹控制，但是对于滑模切换项系数采用预估上界的方法给定，因而控制量存在较大的抖振；文献[5]给出了在Serret-Frenet标架下的船舶运动方程，通过坐标变换可以将曲线路径跟踪问题转换为直线路径跟踪问题，再直接利用神经网络进行控制，设计方法较为繁琐；文献[6]同样给出了Serret-Frenet标架下船舶航迹控制，但是由于采用精确反馈控制，鲁棒性较差；文献[7]给出了基于输入输出线性化的重定义输出变量的航迹控制方法，并在理论上推导了系统全局渐近稳定时的充分条件.

本文在文献[1-6]研究成果的基础上，结合重定义输出变量和神经滑模控制算法，设计了一个自适应神经滑模路径跟踪控制器.利用滑模控制的设计简便性，结合神经网络对非线性系统的强大映射能力，有效地消除趋近律滑模控制对被控对象模型的依赖性.并设计了状态观测器，减少船舶状态量测量所带来的扰动和噪声.最后理论上证明了系统的全局渐近稳定性，仿真结果表明该控制器具有较好的性能.

1船舶路径跟踪模型

欠驱动船舶运动的数学模型描述如下[8]

(1)

式中：x,y,φ为船舶的位姿状态量，分别表示纵向位置、横向位置和航向角;u为船舶前进速度;v为船舶的横荡速度;ω为航向角速度;mii(1≤i≤3)，dii(2≤i≤3)为船舶模型参数;控制输入Tr为首向力矩.本文的控制目标是给定期望航迹，设计控制量Tr，使船舶能从任意初始偏差位置处跟踪上设定轨迹，其跟踪原理图见图1.

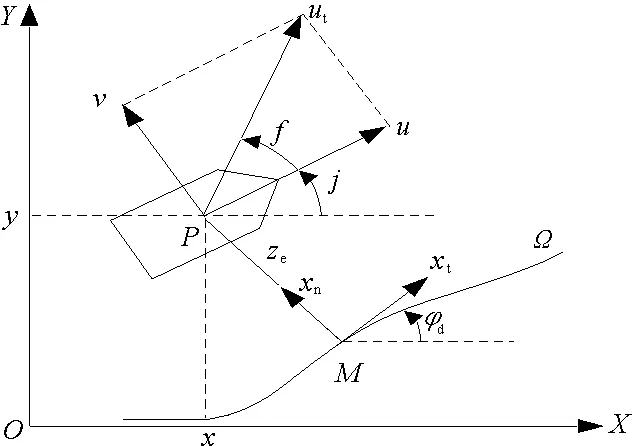
图1　欠驱动船舶路径跟踪原理

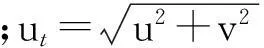
(2)

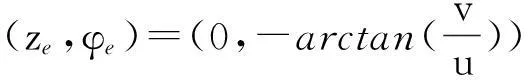
(3)

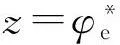
(4)

可得到新的状态方程如下.

(5)

式中：

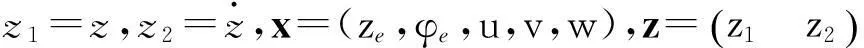
(6)

式(6)的控制目标是设计控制输入量Tr，使得z=0.

2船舶路径跟踪控制器设计

2.1状态观测器设计

在恒定速度下，若令x=[φ,v,w]T，定义输出y=φ=Cx，则有

(7)

设计状态观测器为

(8)

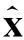
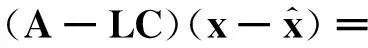
(9)

因此只要设计L使得式(8)全局渐近稳定，即可实现对式(7)状态的重构，利用极点配置算法设计L，此处略.

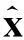
(10)

2.2滑模控制器设计

对式(10)设计基于指数趋近律的滑模控制器，滑模切换函数为

(11)

趋近律为

(12)

(13)

(14)

(15)

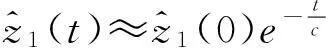
(16)

2.3神经滑模控制器设计

由于受外界干扰及对象参数本身的不稳定性，f和g不易求得，利用RBF神经网络能够从期望的精度逼近任何连续映射[11]，设计RBF网络用于逼近滑模控制律式(14).

神经网络径向基向量h=[h1h2…hn]T，式中：n为隐含层节点数目；hj为高斯基函数.

(17)

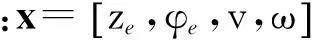
(18)

设神经网络的整定指标为

(19)

式中：r(t)为期望输出；y(t)为实际输出.对于神经网络的权值及参数，可采用最小梯度下降学习算法进行调整，如下式

(20)

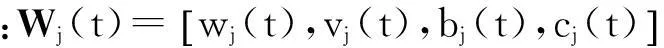
(21)

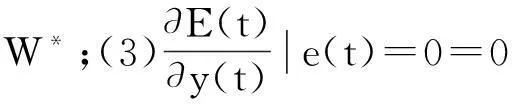
定义神经网络模型的输出为

(22)

定义神经网络整定指标为

(23)

由式(20)可得神经网络的权值及参数学习规则

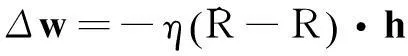
(24)

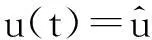
(25)

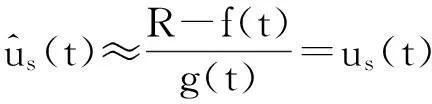
(26)

由定理1可知，在神经滑模控制律式(18)的控制下，式(10)可以趋于稳定，同时式(6)趋于稳定.由于控制律式(18)不需要对象的精确参数，因此在存在干扰的情况下，式(6)是趋于稳定的.

3仿真与分析

针对标称情况及存在外界干扰和参数摄动两种情况下分别进行仿真，以文献[2]中的船为例进行仿真设计，仿真参数如下.

m11=1.2×105kg，m22=1.779×105kg，m33=6.36×107kg，d22=1.47×105kg·s-1，d33=8.02×106kg·s-1，u=10m·s-1.

3.1控制器参数设定

本文涉及的主要参数是神经滑模控制器参数的选择以及重定义输出变量式(4)中k的选择.其中滑模控制器参数设定为：c=0.2，q=20 000，ε=50，k=0.012.RBF神经网络隐层节点数为10，初始权值w=ones(1,10)，v=ones(1,10)，网络结构为b=10×ones(1,10)，c=zeros(4,10).

考虑到实际船舶在海上航行时主要受海浪干扰的影响，因此对海浪进行数值仿真.本文采用基于P-M谱的海浪模型[12]，并采用能量等分法进行海浪建模，经计算得到5级海况下，遭遇角为30°时，海浪对首摇力矩的干扰量，如图2所示.

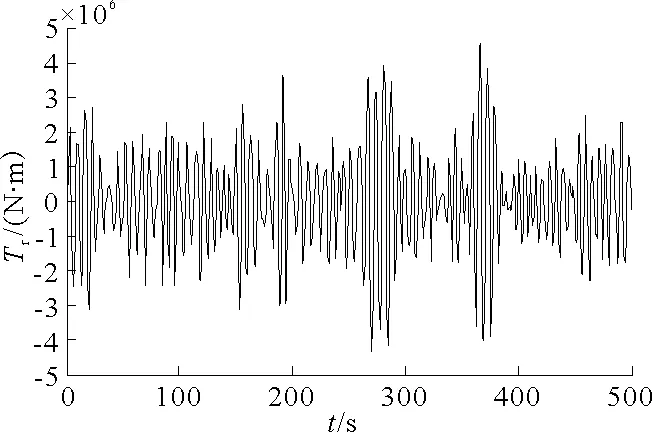
图2　5级海况海浪作用下的干扰力矩

3.2仿真结果

本文所设计的控制器既适合对曲线航迹的跟踪，也适用于对直线航迹的控制.将期望航迹设定为圆，设定的半径r=80 m，期望船舶航迹的表达式为xr(t)=rsinφd，yr(t)=-rcosφd，并设定船舶的初始状态为x=100m，y=0m，φ=0.52rad，w=0rad·s-1，v=0.12m·s-1，仿真结果见图3～4.

图3　船舶在(x，y)平面内的运动轨迹

图4　船舶控制首摇力矩

3.3仿真分析

图3表明，在标称情况下，船舶航行轨迹能较快地以较小的误差跟踪上预定路径，且稳定性较好；在存在干扰及参数摄动时，仍能较快地跟踪上参考路径.

图4表明，在标称情况下，控制器的输出艏摇力矩曲线平滑、大小合理，并最终稳定在一个特定的值上.在存在外界干扰和参数摄动的情况下，输出首摇力矩能够抑制海浪的干扰，使船舶以一定精度运行在设定路径上.

4结束语

本文在基于Serret-Frenet框架下船舶的运动方程，采用RBF神经网络逼近控制对象中的非线性以及不确定部分，实现了设计与对象模型和参数分离，具有较强的鲁棒性；考虑到船舶航行时速度量测量的可操作性较低，设计了状态观测器，利用船舶的航向角重构了船舶横荡速度及航向角速度，最后在simulink平台下用实船参数进行了仿真，仿真结果表明，控制器具有较好的鲁棒性能.

参 考 文 献

[1]BACKSTEPPING N.Ship course controller[J].International Journal of Automation and Computating,2009,6(3):277-284.

[2]LIU Wenjiang,SUI Qingmei,XIAO Hairong,et al.Sliding backstepping control for ship course with nonlinear disturbance observer[J].Journal of Information & Computational Science,2011(8):3809- 3817.

[3]刘杨，郭晨，沈智鹏,等.欠驱动船舶路径跟踪的神经网络稳定自适应控制[J].控制理论与应用，2010，27(2):169-174.

[4]朱齐丹，于瑞亭，夏桂华,等.风浪流干扰及参数不确定欠驱动船舶航迹跟踪的滑模鲁棒控制[J]. 控制理论与应用，2012，29(7):956-964．

[5]段海庆，朱齐丹.基于反步自适应神经网络的船舶航迹控制[J].智能系统学报，2012，7(3):1-8.

[6]王志文，彭秀艳，王大巍.Serret-Frenet框架下欠驱动船的输出反馈路径跟踪鲁棒控制[J].船舶工程.2010，32(6):24-28.

[7]周岗，姚琼芸，陈永冰,等.基于输入输出线性化的全局直线航迹控制[J].控制理论与应用,2007，24(1):117-121.

[8]ZHANG Lijun, JIA Heming, QI Xue, NNFFC-adaptive output feedback trajectory tracking control for a surface ship at high speed[J].Ocean Engineering. 2011,38(13): 1430-1438.

[9]SKJETNE R,THOR I.Fosen.Nonlinear maneuvering and control of Ships[C].//Proceedings of OCEANS 2001 MTS/IEEE Conference and Exhibition, 2001:1808-1815.

[10]刘金琨．滑模变结构控制MATAB仿真[M]．北京：清华大学出版社，2005.

[11]胡德文，王正志，王耀南,等.神经网络自适应控制[M].长沙：国防科技大学出版社，2004.

[12]党祎.基于神经网络的船舶航向PID控制研究[D].哈尔滨：哈尔滨工程大学，2011.

中图法分类号：TP183

doi:10.3963/j.issn.2095-3844.2015.01.041

收稿日期：2014-07-09

Neural Sliding Mode Control for
Tracking of Ships under Serret-renet Frame

LI XiangpingWU HansongRUAN Miaofeng

(CollegeofElectricalEngineering,NavalUniversityofEngineering,Wuhan430033,China)

Abstract：Aiming at the problem of path following of underacuated ships at a constant speed, a neural sliding mode algorithm based on input-output linearization under serret-frenet frame was designed. This algorithm uses the deduction form of ship motion equation under serret-frenet frame to converts the problem above into a case similar to straight line path following and employs neural network to optimize approaching law sliding mode control(ALSMC). It solves the dependency on system model of ALSMC and then improves the robust of controller. To eliminate the influence on control effect brought by measurement error of system state variables, a state observer was designed to reconstruct states of the controlled plant. Simulations on the condition without disturbance and with disturbance also with parameters perturbation indicate that this control law has a good performance index.

Key words：underactuated surface ships；path following; input-output linearization; neural siding-mode control