基于区间数学理论和贝叶斯网络指标灵敏度分析*

张马兰　刘君强　左洪福　谢吉伟　吴　骥

(南京航空航天大学民航学院　南京　210016)

基于区间数学理论和贝叶斯网络指标灵敏度分析*

张马兰刘君强左洪福谢吉伟吴骥

(南京航空航天大学民航学院南京210016)

摘要：针对航空公司安全质量管理体系(SQMS)中风险识别与可靠性改进问题，文中提出基于区间数学与贝叶斯网络的灵敏度分析方法.给出了衡量航空公司安全状况的指标；借助贝叶斯网络建立指标关联网络，结合先验知识进行参数学习以获取条件概率；通过贝叶斯双向推理机制和区间数学理论分析不同区间内重要指标与系统整体安全状况间的扰动关系；基于扰动分析结果对各指标进行灵敏度排序以识别风险并指导可靠性改进工作.实例分析验证了基于区间数学与贝叶斯网络的指标灵敏度分析方法的有效性.

关键词：区间数学；贝叶斯网络；灵敏度；安全质量管理；可靠性

张马兰(1990- )：女，硕士，主要研究领域为民航交通信息控制与管理

0引言

2008年，中国民航局明确要求各航空公司建立健全安全管理体系(safety management system,SMS)[1].将安全与质量统筹考虑，建立安全质量管理体系(safety and quality management system,SQMS)成为航空公司保障安全与寻求发展的重要途径.改善指标可靠性提高系统可靠性，将安全关口前移，方可实现“结果导向式管理”向“风险识别”的转变.因此，对SQMS各指标的灵敏度进行分析以确定其对系统安全状况的影响程度极为重要.

灵敏度分析的实现方法主要包括：统计回归、层次分析、模糊综合评价[1]、证据理论[2]、神经网络等[3-4].统计回归与层次分析难以处理模型属性较多或系统非线性的情况，因为精度难以保证.模糊评价不能处理信息重复性问题.证据理论难以实现区间内赋值.神经网络由于缺乏定量数据的支持仍是一种定性的方法. 本文提出了基于区间数学与贝叶斯网络[5]的灵敏度分析方法.基于区间数学[6]的灵敏度分析，可根据指标在一定幅度内的变化与系统安全状况变化的对应关系，掌握指标的灵敏度.灵敏度分析可以定量分析影响SQMS安全状况的主要因素，以实现风险识别与可靠性改进.

1指标分析

人员、飞机、环境与管理是系统安全的4大基石，只有4者协调发展才能提高系统的可靠性. 根据人机环管理论和民航规则与标准,以及国内外实践经验，结合航空公司的充分数据，建立安全质量管理指标体系，见图1.

对SQMS中的各项指标进行改进并不都是经济可行的，因此，选择8个对系统安全状况有较大影响且在可靠性改进的操作中易实现的指标作为灵敏度分析对象： (1)E,严重维修差错万时率=严重差错次数×104/飞行小时数；(2)F,一般维修差错万时率=一般维修差错次数×104/飞行小时数；(3)G,机务报告故障率=维修人员检查发现故障次数/飞行小时数；(4)H,SDR,统计周期内维修过程中发现的缺陷和不适航状况次数(次/d)，其中，外来物打击和维修差错除外；(5)I,重复性故障=同一架飞机在10 d出现3次或3次以上相同故障的次数；(6)J,故障保留情况=统计周期内所选飞行架次总故障保留数/所选飞行架次；(7)K,机组报告故障率=机组报告故障次数/飞行小时数；(8)L,航班不正常千次率=航班不正常次数/起落次数.

图1　安全质量管理指标体系

2贝叶斯网络

贝叶斯网络(bayesian network,BN)[7]是基于概率论与图论的一种不确定性知识表达与推理模型.有向图中每个原因变量和结果变量都由节点表示，节点间的有向边表示变量间的依赖关系.每个节点均有条件概率表，表征该节点与相邻节点所有可能的条件概率.见图2.

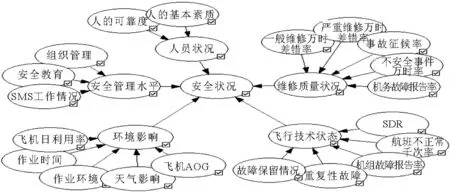
图2　贝叶斯网络结构

1) 条件概率与联合概率条件概率的计算基于链规则，利用变量间的条件独立关系将联合概率分解成复杂度较低的概率分布，从而降低模型复杂度，提高推理效率.

假设A,B为随机事件且P(A)>0，P(B)>0，则A在B发生时的条件概率可表示为

(1)

或

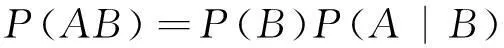
(2)

式(2)表示A和B同时发生的概率等于B发生的概率乘以B发生时A发生的概率，也可表示为

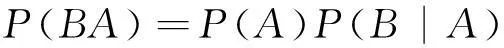
(3)

假设B是由相互独立的事件组成的概率空间{b1,b2,…,bn}，则P(A)可表示为

(4)

联合概率P(X1,X2,…,Xn)是指多个随机变量X1,X2,…,Xn分别满足各自条件的概率.联合概率分布可由各自的局部条件概率相乘得出.

(5)

2) 概率推理概率推理是后验概率的计算过程，其利用随机变量间的条件独立性，将一个联合概率分布直观地表达为一个图形结构和一组条件概率表，经过消元法可计算任意变量的边缘概率.在已知某些证据的情况下，还可以计算感兴趣的节点变量的条件概率分布.贝叶斯网络涉及的概率有先验和后验之分.先验概率是指在考虑“观测数据”前，能表达某一不确定量的不确定性的概率分布，通常是结合先验知识进行主观猜测得到的.后验概率指的是已知贝叶斯网络中某些变量的相关证据或数据，计算另外一些变量的条件概率.通常，贝叶斯推理可以分为2大类，从原因推知结果称为预测推理，从结果推知原因称为诊断推理，常用于故障诊断.

基于网络结构与条件概率，可实现贝叶斯正向推理和反向推理，其优点有：综合先验信息与后验信息；处理不完整数据集；易发现数据间的因果关系；高效推理算法与成熟软件.

3灵敏度分析

灵敏度分析(sensitivity analysis)假设模型表示为y=f(x1,x2,…,xn)(xi为模型的第i个属性值)，研究这些属性的变动对模型输出值的影响程度，是一种定量描述模型输入变量对输出变量的重要性程度的方法.鉴于传统灵敏度分析的不足，本文将区间数学理论引入SQMS指标灵敏度分析中，对于在一定范围内变化的评估参数，将其作为“区间数”进行处理，从而可以全程考虑参数的不确定性，进行一次区间安全状况计算，得到指标灵敏度.

定义系统安全状况的表达式为

(6)

式中:x1,x2,…,xn为各指标的参数，以x0=(x10,x20,…,xn0)为中心的参数变化区间为

(7)

式中:[xi]=[xi0-Δxi,xi0+Δxi],i=1,2,…,n.

由区间数学中区间扩张的性质，对区间参数[xi]=[xi0-Δxi,xi0+Δxi],i=1,2,…,n进行扩张，可得

(8)

将[xi0]=(x10,x20,…,xi0-1,[xi0],xi0+1,…,xn0),i=1,2,…,n代入式(8)，可得

(9)

因此，相对区间灵敏度为

(10)

相对区间灵敏度可解释为某一指标参数变化引起的系统安全状况的变化.通过计算各个指标r(Exi0)值的大小，即可获得敏感性系数.

4实例分析

实例数据来自东方航空公司“安全状况和维修质量管理评估系统”项目.在贝叶斯网络图中，将每个节点的状态定义为好与差2个等级.根节点条件概率通过统计航空公司样本数据中相应事件发生的频次获得.

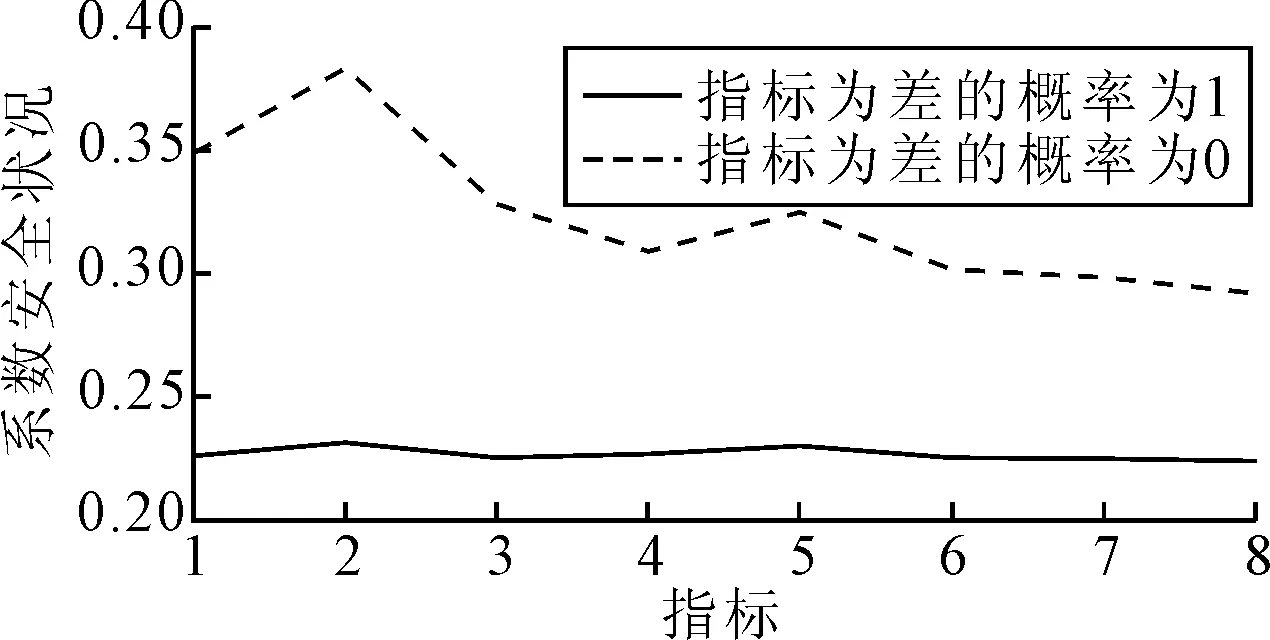
图3　各指标变化对系统安全状况的影响

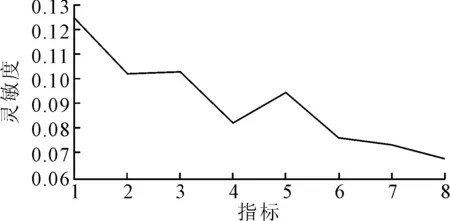
图4　各指标的敏感性系数

根据A为差的概率变化幅度对各指标灵敏度从大到小排序为：E,G,F,I,H,J,K,L.所以，优先对严重维修万时差错率指标进行优化时，能够以最小的投入换取最大的效益.此外，一般维修万时差错率与机务报告故障率的优化也能较大提升系统的安全状况.

2) 正向验证分别对8个指标为差的概率为0.4和0.6，对A为差的概率进行推理.结果见表1.

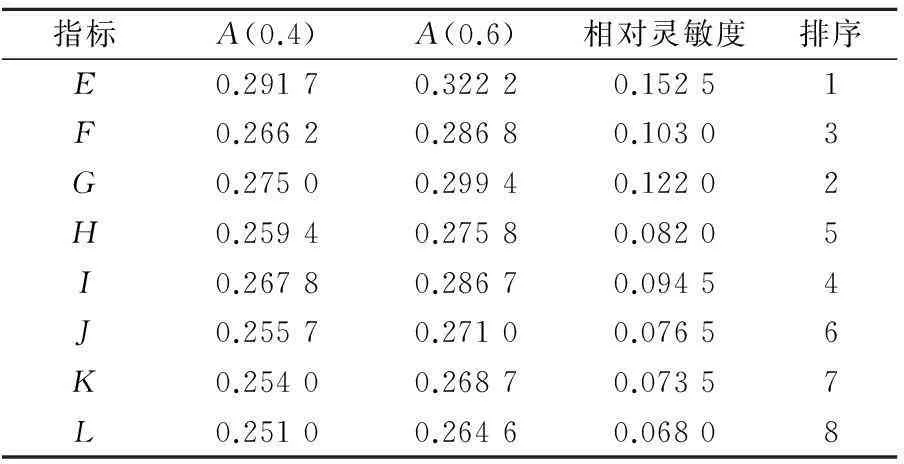
表1　区间数为0.4和0.6时的灵敏度分析

A(0.4)表示指标为差的概率为0.4时系统安全状况为差的概率.表1表明，各指标灵敏度排序与以上推力结果相符.

3) 反向验证对A为差的概率为1时推理各个指标为差P1和为好P2的概率，结果见表2.

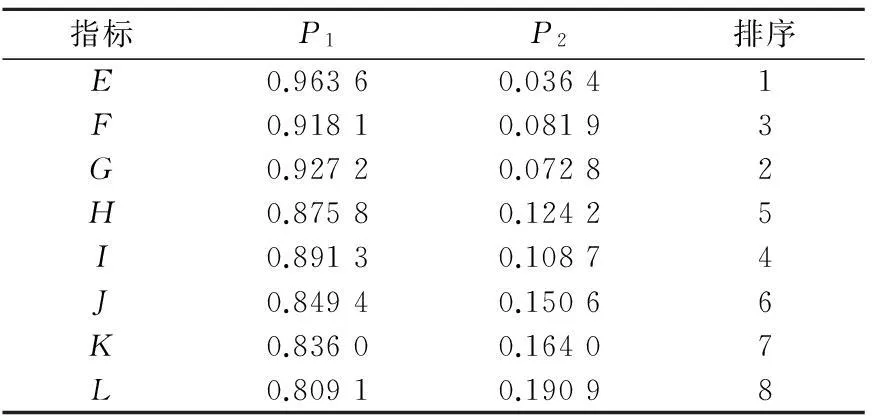
表2　总体安全质量为差时各个指标

表2说明，反向推理机制下得到的灵敏度分析结果与正向推理是一致的.

4) 应用举例图5是航空公司2011年1月～9月的安全状况统计结果，9月份的系统安全状况为好的概率低于警戒值下限，说明该月需对系统指标进行优化.利用式(10)，计算将总体安全状况为好的概率从0.79提升至0.85时各个指标单独调整所对应的指标敏感性系数，见表3.

因此，优化时应按照E，G，F，I，H，J，K，L的

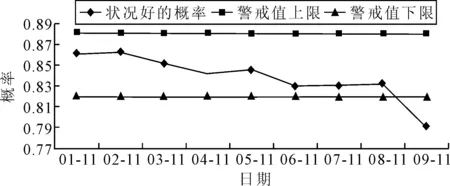
图5　2011年安全状况为好的概率分布

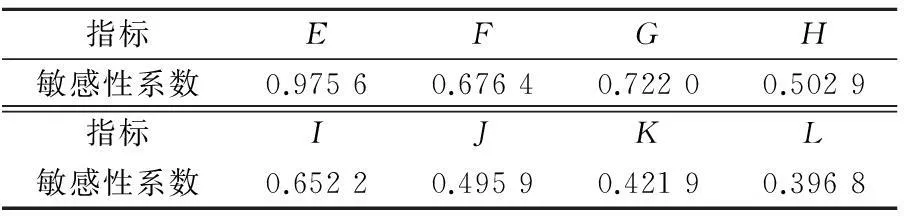
指标EFGH敏感性系数0.97560.67640.72200.5029指标IJKL敏感性系数0.65220.49590.42190.3968

优先顺序进行指标调整.实际上，不可能对上述所有的指标同时调整或者只调整敏感性系数最大的指标.因此，需要计算组合指标敏感性.假设对各个指标的调整量为0.05，分别计算组合E，EG，EFG,EFGI,EFGHI,EFGHIJ,EFGHIJK,EFGHIJKL的敏感性系数，结果见表4.

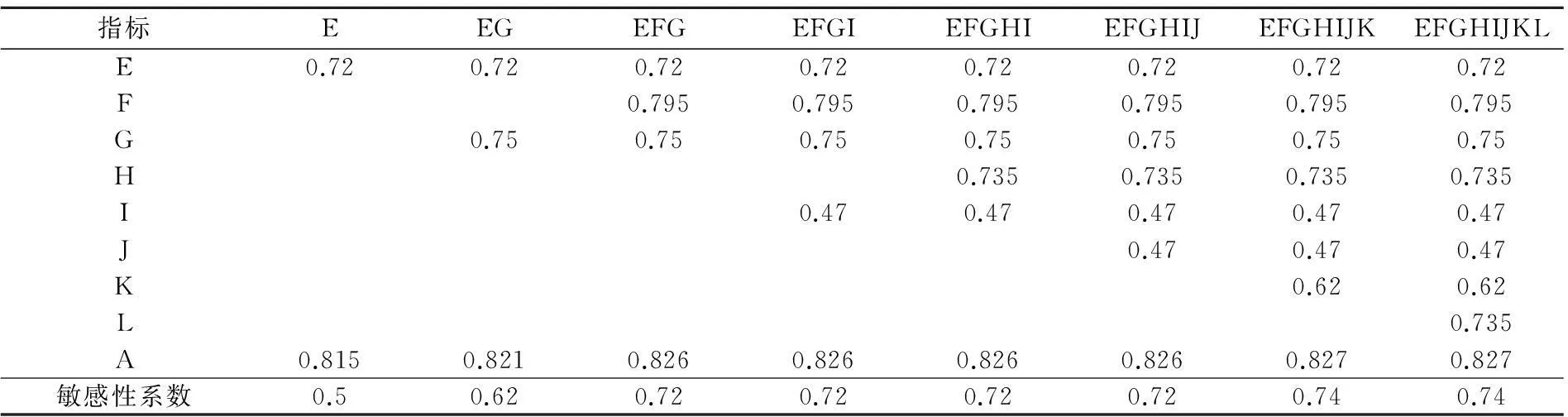
表4　组合指标的相应调整量与敏感性系数

可见，要想以最小的调整换取最大的安全状况提升应当对严重维修万时差错率、机务报告故障率以及一般维修万时差错率3个指标同时进行调整.含有I,H,J,K,L指标的组合灵敏度较低，因此不建议对其进行优化.

5结束语

本文将基于区间数学与贝叶斯网络的灵敏度分析方法应用于航空公司安全质量管理体系，采用贝叶斯网络建立指标因果关联，结合实际数据通过参数学习确定节点条件概率，借助区间数学与贝叶斯推理对安全状况的概率进行推理最终确定了各指标的灵敏度.研究结果可用于确定系统可靠性的主要影响因素并为航空公司提供安全管理决策依据，因此对提升航空公司安全质量管理的能力，以及推动民航业的健康发展具有重要意义.在将来的研究中，考虑基于区间数学与动态贝叶斯网络研究灵敏度分析方法.

参 考 文 献

[1]金灿灿,左洪福,张营,白芳.基于BBN的航空公司风险评估技术研究[J].航空学报,2012，34(3):588-596.

[2]丁松滨，石荣，施和平.基于证据理论的航空公司安全系统风险评价[J].交通运输系统工程与信息,2007,7(2):38-41.

[3]JULIAND,OLDENDA.JACKSON.Illuminatingtheblackbox:arandomizationapproachforunderstandingvariablecontributionsinartificialneuralnetworks[J].EcologicalModeling,2002,154:135-141.

[4]SOBOLIM.Sensitivityestimatesfornonlinearmathematicalmodels[J].MathModeling&ComputationalExperiment,1993(1):407-420.

[5]郑珂珂.航空公司安全状况和维修质量管理安全评估技术研究[D].南京:南京航空航天大学,2012.

[6]李冬,瞿朝辉,马海洋.作战效能灵敏度分析的区间方法[J].电光与控制,2011,18(7):1-4.

[7]NIMAK,FAISALK,PAULA.Safetyanalysisinprocessfacilities:ComparisonoffaulttreeandBayesiannetworkapproaches[J].ReliabilityEngineeringandSystemSafety,2011,96(8):925-932．

中图法分类号：U8

doi:10.3963/j.issn.2095-3844.2015.01.037

收稿日期：2014-10-10

SensitivityAnalysisforIndicatorsBasedon
BayesianNetworkandIntervalMathematics

ZHANGMalanLIUJunqiangZUOHongfuXIEJiweiWUJi

(College of Civil Aviation, Nanjing University of

Aeronautics and Astronautics,Nanjing 210016,China)

Abstract：To meet the requirements of risk identification and reliability engineering proposed by Safety and Quality Management System (SQMS), this paper presents a novel approach to sensitivity analysis by combining Bayesian network with interval mathematics. Firstly, the security status indicators of the airlines are given. Then, Bayesian network is utilized to construct a directed graph for these indicators, and prior knowledge is taken into account for parameters learning to obtain conditional probability table (CPT). After that, interval mathematics and Bayesian bidirectional inference mechanisms are incorporated for the analysis of the interaction between the indicators and the overall security level. Finally, according to the obtained interaction, sensitivity analysis can be achieved to provide a guide for operators to implement risk identification and reliability engineering. A case study is presented to verify the effectiveness of the novel sensitivity analysis method in SQMS for airlines.

Key words：interval mathematics; bayesian network; sensitivity; safety and quality management; reliability

*国家自然科学基金重点项目(批准号：61232002)、国家自然科学基金委与中国民用航空总局联合项目(批准号：60939003)、中国博士后面上基金项目(批准号：2012M521081)、中国博士后基金特别资助项目(批准号：2013T60537)、中央高校基本科研业务项目(批准号：NS2014066)、江苏省博士后基金项目(批准号：1301107C)资助