流固耦合作用对螺旋桨强度影响的数值计算*

任　弘　李范春　杜　玲

(大连海事大学交通运输装备与海洋工程学院　大连　116026)

流固耦合作用对螺旋桨强度影响的数值计算*

任弘李范春杜玲

(大连海事大学交通运输装备与海洋工程学院大连116026)

摘要：为研究流固耦合作用对船舶螺旋桨强度的影响，并分析采用不同流固耦合方法所得计算结果的差异，结合实际工程，使用CFX对某船螺旋桨在特定工况进行CFD计算，并在ANSYS WORKBENCH中分别运用单向流固耦合和双向流固耦合方法对螺旋桨静应力及总变形量进行计算分析和比较，给出螺旋桨表面压力分布图，以及等效应力和总变形量随螺旋桨桨叶半径变化的关系曲线，并将二者计算结果进行对比.结果表明,采用不同流固耦合方法所得应力应变分布基本一致，最大等效应力出现在桨叶随边靠近桨毂处，叶梢位置变形最大.两种方法中采用双向流固耦合方法所得等效应力和总变形量峰值较大，且随着进速系数的增大，二者计算结果差距逐渐明显.

关键词：船用螺旋桨；静应力分析；流固耦合；有限元仿真

任弘(1990- )：男，硕士，主要研究领域为船舶结构

0引言

船用螺旋桨在水中工作时，受力情况较为复杂，不仅要承受重力、离心力，还要承受流体作用力.流体作用力会以压力形式传递给螺旋桨，引起螺旋桨结构变形，而结构变形又会使外部流场发生变化.双向流固耦合方法是在流场和结构场之间设置流固耦合面(FSI)，把流体计算的结果作为载荷导入到结构中计算，随后将结构计算得出的位移和温度通过流固耦合面传递回流体中进行计算，使得流场耦合面与结构耦合面上的网格相互映射以实现数据传递[1].双向流固耦合考虑了结构变形对于流场的影响，计算精度较高，但计算周期较长.相比而言，单向流固耦合计算所需时间、资源较少，适用于结构变形不足以显著改变流场的情况，仅将流体计算所得结果作为载荷施加到结构场中，不将结构所得计算结果传递给流体，计算过程相对简单.

近些年来，国内外学者开展了流固耦合方面的研究工作：Khalid等[2]基于ANSYS-CFX，采用双向流固耦合法，对垂直轴风机转子进行瞬态流固耦合响应模拟，采用双向流固耦合方法的计算结果更接近试验值，在大变形计算中更为明显；Jo等[3]采用单向流固耦合法，对风力发电机进行模拟，得出速度和流线的分布云图，计算出应力应变以及安全系数，为日后振动及瞬态动力学分析提供参考；Young等[4]基于ABAQUS，利用边界元法计算出刚性叶片旋转所导致的水压力，考虑水压力、离心力,以及科氏力，利用有限元法对复合材料螺旋桨进行结构计算，计算所得变形值返回到边界元程序中更新桨叶几何形状，迭代直至结果收敛，该方法可以预测弹性复合材料螺旋桨的桨叶水力负荷、空泡图形和应力应变分布；Montely等[5]采用Young的方法，设计了复合材料螺旋桨，通过实验证实该桨具有比传统螺旋桨更优的推进性能.

本文采用ANSYS-CFX单向流固耦合和双向流固耦合方法，对某船螺旋桨在特定工况下的等效应力和总变形量进行了计算分析、比较，着重探讨了2种方法模拟分析结果的异同，给出了螺旋桨表面压力分布情况，以及等效应力和总变形量随桨叶半径变化的关系曲线，能够较为准确地实现螺旋桨强度预测，对于预防疲劳破坏、提高螺旋桨运行稳定性有着重要意义.

1理论背景

1.1流场数值计算

对于三维粘性湍流流体的连续性方程和基于RANS的动量方程可以表示为

连续性方程：

动量方程：

式中：ui，uj为速度矢量；为流体密度；p为流场静压；μ为分子粘度为Reynolds应力，根据Boussines涡粘性假设,

其中：μt为湍动粘度；k为湍动能；δij为Kroneckerdelta符号.

采用SSTk-ω湍流模型[6].

式中：φ1为Standardk-ε湍流模型；φ2为Standardk-ω湍流模型；φ3为SSTk-ω湍流模型；F1为近壁面和远离壁面的混合函数，以实现SSTk-ω模型在近壁面和远离壁面自动转换使用Standardk-ε模型和Standardk-ω模型.

1.2流固耦合静力分析有限元方程

静力学有限元方程：

Ku=F

式中：K为螺旋桨的刚度矩阵；u为螺旋桨节点位移矢量矩阵；F为螺旋桨所受载荷，由离心力，重力,以及由CFD中计算所得的流体压力组成.

瞬态动力平衡方程

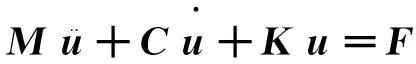
式中：M为质量矩阵；C为阻尼矩阵.

2有限元模型与边界条件

2.1三维建模及网格划分

根据某船螺旋桨曲面型值，通过坐标变换的方法，利用MATLAB软件计算，将螺旋桨叶切面的二维坐标值按照文献[7]反推导出螺旋桨三维叶切面空间坐标点.然后将计算得到的三维空间坐标点导入UG，利用UG的曲面建模技术，进行实体几何建模，将实体模型导入ANSYS WORKBENCH中，使用Enclosure命令分别生成包覆在螺旋桨周围的旋转域和静止域[8].螺旋桨周围流场计算域示意图见图1，螺旋桨的主要参数见表1.

图1　螺旋桨周围流场计算域示意图

直径/m螺距比盘面比叶数旋向n/(r·min-1)ρ/(kg·m-3)E/GPaυ5.60.70.54右旋12474001240.33

流体域分为旋转域和静止域2个部分，内部旋转域采用非结构化四面体网格，对螺旋桨桨叶、桨毂处壁面进行加密处理，外部静止域采用结构化六面体网格.旋转域与静止域采用滑移网格，通过定义interface边界来传递两边不同网格的数据，采用Frozen Rotor模型，网格关联为GGI方式连接.

由于螺旋桨叶片是形状不规则的复杂曲面，为了能更好的模拟，结构域网格使用ANSYS WORKBENCH自带的网格划分模块MESH对模型进行自适应网格划分，对网格尺寸进行调节，以提高网格的质量,见图2.

图2　螺旋桨网格划分

2.2湍流模型的选择

螺旋桨工作时周围流场十分复杂，为了保证计算精度需要选择合理的湍流模型，目前几种常用的湍流模型有Standardk-ε，RNGk-ε和SSTk-ω.Standardk-ε是工程中应用最为广泛的湍流模型，但在模拟旋转流体、曲面壁流以及平均应变率突变的流体时偏差较大；RNGk-ε模型在Standardk-ε模型基础上增加了一个附加项，用于应对平均流动中的旋转以及大应变率流动；SSTk-ω模型是利用混合函数有效结合了k-ω和k-ε模型的优点，在近壁区采用Standardk-ω模型，而在近壁区以外采用Standardk-ε模型，能获得精度较高的计算结果，并且求解时间接近Standardk-ε模型[9]，效率较高.综合考虑，采用SSTk-ω作为螺旋桨流体计算的湍流模型.

2.3边界条件

对于单向流固耦合，计算域入口为速度入口，由螺旋桨转速和进速系数关系给出，转速为定值，通过调整来流速度实现进速系数的改变；计算域出口为压力出口，给定为静压分布；外边界设定为开放边界；螺旋桨桨叶和桨毂表面定义为不可滑移壁面；旋转域转速与螺旋桨转速相同.

对于双向流固耦合，先要在Transient Structural中进行瞬态动力分析，时间步长和总时间要与在CFX中所设置的时间相同，定义流固耦合面，将其导入CFX即可耦合求解，求解方式为After CFX Fields.在CFX中同样标识流固耦合面，流体网格单元向固体网格节点传递压力，数据类型为Total Forces，固体网格节点向流体单元传递网格位移，数据类型为Total Mesh Displacement.

结构分析中，对螺旋桨施加重力和离心力载荷，将流体压力导入至结构表面，对桨毂施加固定约束.

3计算结果分析

3.1螺旋桨压力分布

图3、图4为螺旋桨进速系数J=0.4时单、双向流固耦合在桨叶表面的压力分布.由图3,图4可见，2种方法的压力分布不同，螺旋桨的变形改变了周围的压力场，采用双向流固耦合方法的正压力、负压力峰值均升高，并且压力分布较均匀.吸力面上最大负压出现在叶梢处，导边区域总压低于随边区域；而压力面上导边区域总压高于随边区域，压力最小值出现在桨叶中部.

3.2螺旋桨的应力分布

为方便比较采用不同流固耦合方法所得应力变化规律的异同，使用Convert to path命令，选取桨叶随边从叶梢到叶根作为路径，生成应力随螺旋桨桨叶半径变化的关系曲线.图5为3种工况时单、双向流固耦合应力变化曲线，虚线为单向流固耦合变化曲线，实线为双向流固耦合变化曲线.由图5可见，应力曲线变化趋势基本一致，在叶梢附近应力值最小，由叶梢到叶根应力逐渐增大，应力分布集中较为显著区域为桨叶随边与桨毂交界处.随着进速系数的增大，等效应力减小.表2为在3种工况单、双向流固耦合等效应力峰值大小比较.

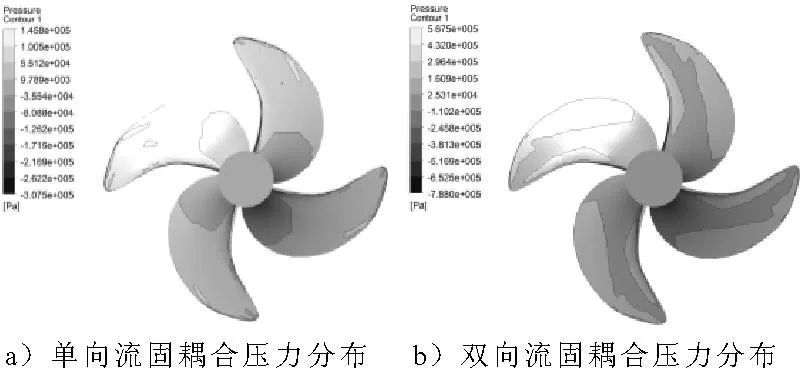
图3　压力面压力分布(J=0.4)

图4　吸力面压力分布(J=0.4)

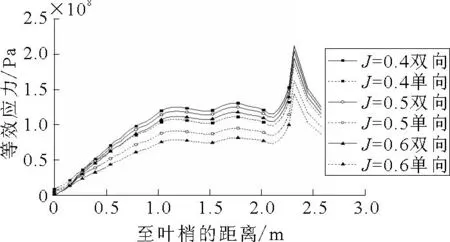
图5　应力变化曲线

MPa

3.3螺旋桨的变形

图6为3种工况时单、双向流固耦合总变形量变化曲线.由图6可见，总变形量曲线变化趋势基本一致，桨叶最大变形位于叶梢处，变形量由叶梢到叶根应力逐渐减小.这是由于叶梢处与流体的相对运动速度较高，形成较大压力，并且叶梢处桨叶厚度几乎为零，叶梢到桨毂距离最大，容易发生形变.随着进速系数的增大，总变形量减小.表3为在3种工况单、双向流固耦合总变形量峰值大小比较.

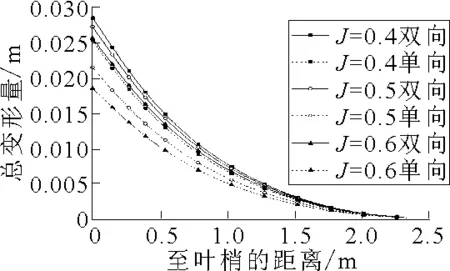
图6　总变形量变化曲线

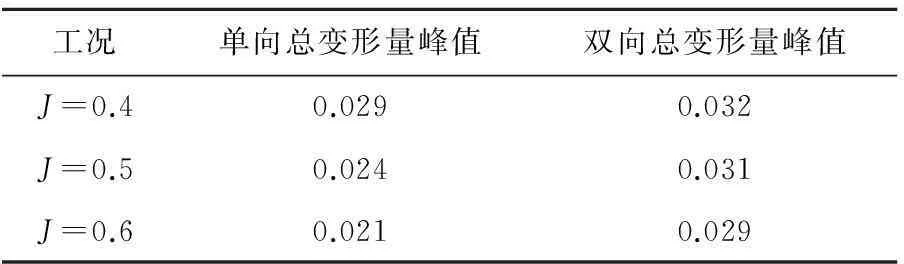
表3　总变形量峰值大小比较　m

3.4误差分析

由表2、表3可知，在各种工况下采用双向流固耦合计算所得等效应力和总变形量峰值均比单向流固耦合大.为方便比较采用不同流固耦合方法对计算结果的影响，在桨叶随边均匀的选取11个点，二者误差见表4.以J=0.4为例，等效应力偏差在-78.23%～17.33%之间，总变形量偏差在12.48%～15.59%之间，随着进速系数的增大，二者计算结果差距变大.

表4　不同流固耦合方法的计算偏差

4结论

1) 采用ANSYS-CFX流固耦合分析能够较为真实准确地反映流体外载荷对螺旋桨强度计算的影响，提高了计算的精度.

2) 采用不同流固耦合方法所得到的螺旋桨表面压力分布迥异，由双向流固耦合方法所得出的表面正、负压力峰值均升高，分布较单向流固耦合更均匀.

3) 最大等效应力发生在螺旋桨桨叶随边根部，在进行疲劳分析时应对这个部分进行校核；压力面与吸力面应力分布不具备对称性；最大变形位于螺旋桨叶梢处；双向流固耦合所得最大等效应力、最大变形量比单向流固耦合所得计算结果大.

4) 通过在特定工况下对比发现，采用不同流固耦合方法对表面压力分布影响较大，而对于应力应变的分布无明显影响，J=0.4时应力计算结果误差在-78.23%～17.33%之间，应变计算结果误差在12.48%～15.59%，并且随着进速系数的增大，计算结果差距更为明显.

参 考 文 献

[1]BENRA F K,DOHMEN H J,PEI J,et al.A comparison of one-way and two-way coupling methods for numerical analysis of fluid-structure interactions[J].Journal of Applied Mathematics,2011 Article ID 853560，[doi:10.1155/2011/853560].

[2]KHALID S S,ZHANG Liang,ZHANG Xuewei, et al. Three-dimensional numerical simulation of a vertical axis tidal using the two-way fluid structure interaction approach[J].Journal of Zhejiang University-Science A, 2013,14(8):574-582.

[3]JO C H, KIM D Y,RHO Y H,et al.FSI analysis of deformation along offshore pile structure for tidal current power[J].Renewable Energy,2013,54:248-252.

[4]YOUNG Y L.Fluid-structure interaction analysis of flexible composite marine propellers[J].Journal of Fluids and Structures,2008, 24: 799-818.

[5]MONTLEY M R,LIU Z,YOUNG Y L. Utilizing fluid-structure interactions to improve energy efficiency of composite marine propellers in spatially varying wake[J].Composite Structures,2009,90:304-313.

[6]SAS IP, Inc .ANSYS theory reference[M].USA,SAS IP,Inc,2012.

[7]吴利红,董连斌,许文海.基于MATLAB和ProE的螺旋桨三维建模[J].大连海事大学学报,2011,37(2):17-20.

[8]CALIFANO A, STEEN S.Numerical simulations of a fully submerged propeller subject to ventilation[J].Ocean Engineering, 2011, 38: 1582-1599.

[9]张帅，朱锡，侯海亮.船舶螺旋桨流固耦合稳态求解算法[J].哈尔滨工程大学学报,2012,33(5):615-621.

中图法分类号：U661.44

doi:10.3963/j.issn.2095-3844.2015.01.033

收稿日期：2014-10-25

Numerical Calculation for the Effect
of FSI on Marine Propeller Strength

REN Hong LI Fanchun DU Ling

(TransportationEquipment&EngineeringCollege,DalianMaritimeUniversity,Dalian116026,China)

Abstract：The objective of this study is to examine the Fluid Structure Interaction (FSI) effect on marine propeller strength and analyze the results of different fluid-structure coupling method, referring to the practical situation of the project, use CFX for marine propeller CFD calculation in a certain condition, calculate and compare the results of equivalent stress and total deformation by different coupling method in ANSYS WORKBENCH respectively, give the propeller surface pressure contour, as well as the equivalent stress and total deformation curves of propeller blade under different radius. The results show that the equivalent stress and the total deformation distribution of different methods are basically the same, the maximum equivalent stress appears on the blade trailing edge near the hub, and the maximum deformation appears on the blade tip position. The maximum equivalent stress and maximum total deformation are larger by using two-way coupling method, along with the increase of advance coefficient, the difference of results between two algorithms is obvious.

Key words：marine propeller; stress analysis; fluid-structure interaction; FEA

*国家自然科学基金面上项目资助(批准号：51379025)