干线公路无控交叉口振动减速标线设计与舒适性评价*

余金林　徐良杰　刘启远　秦亚晓

(武汉理工大学交通学院　 武汉　430063)

干线公路无控交叉口振动减速标线设计与舒适性评价*

余金林徐良杰刘启远秦亚晓

(武汉理工大学交通学院 武汉430063)

摘要：为了降低干线公路无控交叉口处驾驶员超速行驶产生的交通事故，在交叉口处进行振动减速标线设计，并探讨了振动减速标线的参数设计方法.采用改进加权加速度均方根与K值系数法相结合，建立振动频率、振动幅度和车速变化因子的综合舒适性评价模型.针对不同振动减速标线组数和车辆减速度，进行振动减速标线设计，分析不同减速效果下驾驶员的舒适性.

关键词：干线公路；无控交叉口；振动减速标线；振动频率；振动舒适性

余金林(1990- )：男，硕士生，主要研究领域为交通安全

0引言

通过对我国不同的公路交通条件分析，公路交叉口处发生的交通事故占总量的59%，是公路网络中交通安全的瓶颈，而超速行驶是诱发交通事故的主要原因之一[1].超速行为产生的交通事故多为重大和特大交通事故，造成的人员的伤亡和财产损失十分严重.因此，针对公路交叉口的车速控制研究十分必要.

国内外车速控制主要应用于高速公路匝道出入口、长下坡路段和收费站等，车速控制的主要方法包括法规控制、心理控制和工程控制.其中，应用最多的是振动减速标线和视错觉标线.颜先华等[2-3]在视错觉标线的形状、间距、尺寸,以及减速效果等方面进行了大量的研究，但是在长效机制作用下，视错觉减速效果会减弱，而且设置过多的视错觉标线容易引起驾驶疲劳.候树展等[4-5]通过实地实验并且统计分析，得出了振动减速标线的减速效果,以及减速规律.杜志刚等[6]提出了基于视错觉的振动减速标线设计方法；袁振友，唐江[7-8]讨论了一级公路交叉口处振动减速标线的设置方式，并给出了标线的大致间距尺寸，但是缺乏间距尺寸的具体设置分析.在研究汽车平顺性评价时，Pennati等[9]给出了人体坐姿和立姿下的振动评价方法，并给出了加权加速度均方根(RMS)评价指标；Janeway[10]以振动频率和振幅为主要影响因素建立舒适性评价模型，并给出相应的舒适性评价标准，但是针对振动减速标线与驾驶员舒适性之间的关系研究比较缺乏.

综上所述，振动减速标线在高速公路匝道、转弯处，以及一级公路交叉口的应用十分广泛，但是缺乏振动减速标线的具体设计方法，同时也缺乏对设计后的振动减速标线舒适性评价.

因此，探讨分析在不同振动标线组数和车辆减速度下，干线公路无控交叉口功能区的振动减速标线具体设计方案，通过振动警示进行车速控制，确保车辆以安全车速通过交叉口，并对不同设计方案进行振动舒适性评价，为干线公路无控交叉口的振动减速标线优化设计提供依据.

1振动减速标线设计方法

1.1前提条件

根据文献[11]，以及汽车制动性能、公路条件、司机反映特性，振动减速标线设计需满足以下条件：(1)车辆通过减速标线参数按照车辆以1.8 m/s2～3 m/s2的减速度进行设计，且通过振动减速标线区域的车辆做匀减速运动；(2)为了保证振动节奏感，每道减速标线间隙和标线本身宽度相等；(3)为了保证乘客和驾驶员的舒适性，车辆通过各组标线间隔时间应该大致相等.

1.2线条宽度

已知，小汽车轴距为2.2～2.8 m，大车轴距5.6 m，为了不至于前轮和后轮同步感受振动而降低节奏感和振动效果，每组振动减速标线宽度小于2.2 m才能满足小汽车和大车的振动警示效果.假设每组振动减速标线设置3道，为了保持节奏感，每道减速标线间隙和标线本身宽度相等，于是每道标线宽度应该小于2.2/(3+2)=0.44 m.根据汽车合理振动频率,以及振动节奏感和减速要求，每道标线设置0.3 m时最符合，因此，取振动减速标线的线条宽度0.3 m.

1.3凸起高度

根据研究表明，方形点状凸起减速效果好.因此，主要考虑将交叉口前振动减速标线的凸起设置为方形点状，并且结合振动减速标线设计规范，将凸起高度设置为3～8 mm.

1.4振动减速标线区长度

车辆驶入干线公路进入交叉口的初始车速设为v1，到达交叉口前控制车速v0.根据运动学公式可以确定振动减速标线区的长度.

(1)

式中：s为振动减速标线区域总长度；v1为车辆进入振动减速标线前车速；v0为车辆通过振动减速标线后车速；a为车辆采取的减速度.

1.5相邻标线组距

由于车辆通过每组振动减速标线的时间是相同的，根据运动学公式可以确定相邻2组振动减速标线的间距.

(2)

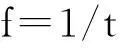
(3)

(4)

(5)

式中：t为车辆通过相邻组标线的时间；f为振动减速标线的频率；n为振动减速标线的组数；vi为车辆通过第i组振动减速标线时车速，i>1；Δsi为第i+1组振动减速标线和第i组振动减速标线的间距.

2驾驶员舒适性评价模型

影响人体对振动反应的主要因素包括振动频率、振动强度和作用时间.然而，通过分析车辆减速运动的过程，计算得出交叉口处设置的振动减速标线作用的时间不超过10 s，可以忽略作用时间的影响.因此，主要通过振动频率、振幅和车速变化等指标进行驾驶员舒适性评价建模.其中，振动频率和车速变化均与车型无关，振幅与车辆减振系统相关，因此，为了提高模型的精确性，提出不同车辆的振幅修正系数λ.

传统的加权加速度均方根值模型[12]是由振动频率与其功率密度谱函数得出，即

(7)

(8)

(9)

然而，讨论的振动减速标线的振动频率是固定的，而车速是均匀变化的，因此，将上述模型改进得到振动频率因子与车速因子的振动舒适性评价模型.

f=v·n

(10)

(11)

将式(10),(11)代入式(7)～(9)，得到适用于振动减速标线的评价模型，同时结合K值系数法，分别得到振动频率因子与速度因子、振动频率因子与振幅因子的综合振动舒适性评价模型，具体如下.

aw=

(12)

(13)

式中：aw为加速度加权均方根值，m/s2；K为振动舒适性指标值；ω(f)为频率加权函数，f<2 Hz，取值0.5 Hz；Ga(n0)为参考空间频率n0对应的功率谱密度函数,256×10-6；n为空间频率，n0=0.1 m-1；Δsi为第i+1组标线和第i组标线之间的间距；m为振动减速标线组数，取值5,7,9；β为频率指数，一般取2；v为车速；λ为振幅修正系数，与车辆的减振器作用相关，一般取值0.3～1；A为凸起标线高度，mm；f为振动频率.

评价标准：

1) 加速度加权均方根值当aw<0.315 m/s2时，驾驶员没有感觉不舒适；当0.315 m/s2

2)K值系数法当K<1时，驾驶员没有感觉到不舒适；当110时，驾驶员感觉到非常不舒适.

3案例分析

3.1方案设计

由于干线公路无控交叉口是由主线和支线交叉形成，所以主要探讨主线振动减速标线的设计.干线公路在路段的车速可以达到限速值，假定干线公路v1限定为 80 km/h；车辆进入交叉口前需保持安全车速行驶，到达交叉口前控制车速v0限定为20 km/h，为了保证车辆达到控制车速，在交叉口前设置20 km/h的限速标志.根据文献[13]，驾驶员反映到操作时间在0.4～1 s之间，取最大值1 s，制动器制动时间在0.2～0.9 s，平均减速度为3～4 m/s2.代入式(4)中，计算得车辆安全停车距离为15 m，因此第一组减速标线距离交叉口的安全距离为15 m.

振动减速标线宽度取值0.3 m，凸起高度取值3，5，8 mm，按照a=1.8,2.0，2.2，2.4，2.6，2.8，3.0 m/s2的车辆减速度，以及分别采取5,7和9组的设置方案.其中3 mm和8 mm分别是规范要求的最低值和最高值，5 mm为参考值；a=1.8 m/s2是规范要求的最小值，a=3.0 m/s2是规范要求的最大值，其他减速度为参考值；为了保证振动强度的合理过渡，靠近交叉口处的几组减速标线设置2道，远离交叉口的几组设置为3道，见表1.

表1　不同减速度、振动减速标线组数下振动减速标线设计方案

3.2方案评价

利用上述的改进加权加速度均方根与K值系数法结合的双重评价模型，对驾驶员感知振动的舒适性评价，得到评价指标值见图1～3.

评价结果：

1) 当车辆以1.8～3.0 m/s2的减速度进行减速时，利用加速度加权均方根值的舒适性评价模型(振动频率因子和车速因子)得出驾驶员感知的aw均小于0.315 m/s2，振动减速标线并没有对驾驶员产生不舒适感.

2) 当车辆以1.8～3.0 m/s2的减速度进行减速时，利用K值系数法的舒适性评价模型(振动频率因子和振幅因子)得出：当振动凸起高度A小于5 mm时，驾驶员感知的K值一般都大于1且小于10，振动减速标线对驾驶员产生轻微不舒适感；当振动凸起高度A=8 mm，设置9组振动减速标线时，驾驶员感知的K值部分都大于10，振动减速标线对驾驶员产生不舒适感.

图1　车辆减速度与振动频率的关系(m=5、7、9)

图2　不同设计方案的改进加权加速度均方根舒适性评价结果

图3　不同设计方案的K值系数法舒适性评价结果

3)随着减速度值的增大和标线组数的增加，驾驶员感知的K值会增大；当振动凸起高度A超过5 mm时，有部分标线设置方案让驾驶员感知的K值大于10，会产生不舒适性；当振动凸起高度A等于8 mm、车辆以采取的减速度a大于2.4 m/s2时，驾驶员对9组振动减速标线感知的K值均大于10，会产生不舒适感.

4结论

1) 提出了干线公路无控交叉口的振动减速标线设计方法和舒适性评价.改进加权加速度均方根与K值系数法结合的双重评价模型充分的考虑了振动频率、振幅和车速变化对驾驶员感知的舒适性影响，可以为振动减速标线的参数优化设计提供依据，在保证减速效果的前提下，避免振动减速标线产生的不舒适性负面效果.

2) 当振动标线凸起高度小于5 mm时，双重评价模型得出的车辆以1.8～3 m/s2的减速度的舒适性较好，设计的方案均可以接受，当振动标线凸起高度大于5 mm时，宜设置7组以下标线，不宜设置9组标线.

3) 随着振动频率的增加，驾驶员感觉的舒适性逐渐变差，当振动标线凸起高度小于5 mm并且振动减速标线设置9组时，建议车辆采取1.8～2.4 m/s2的减速度进行设计较好.

4) 由于振动减速标线作用于驾驶员的时间较短，忽略了振动时间因素.后续工作需要进一步细化研究振动时间对驾驶员舒适性的影响.

参 考 文 献

[1]吴玲涛,彭道月,沈国华,等. 公路平面交叉口交通事故特点研究[C].第8届汽车交通安全国际会议论文集，长沙：湖南大学，2010：4-9.

[2]颜先华.公路梳齿形视错觉减速标线优化研究[J]. 公路与汽运,2011(5):58-61.

[3]刘浩学.公路视错觉减速标线参数优化[J]. 长安大学学报：自然科学版,2011(6):77-81.

[4]候树展.高速公路振动减速标线路段运行速度变化规律研究[J].中国公路学报，2012,23(2)：255-259.

[6]杜志刚,郑展骥,王自入.基于驾驶员错视觉的振动减速带优化设计[J]. 武汉理工大学学报：交通科学与工程版，2012,36(6):1179-1183.

[7]袁振友．减速振动标线在一级公路平面交叉口的应用[J].公路，2005(4)：55-58．

[8]唐江．一级公路交叉口区域速度控制方法研究[J].中外公路，2011，6(3):104-108．

[9]PENNATI M，GOBBI M，MASTINU G.A dummy for the objective ride comfort evaluation of ground vehicles [J]. Vehicle System Dynamics，2009，47 (3)：355-360.

[10]JANEWAY R.Vehicle vibration limits to fit the passenger[J].SAE Technical Paper 480061,1948,doi:10.4271/480061.

[11]交通部公路科学研究院．JTG D82—2009公路交通标志和标线设置规范[S].北京：人民交通出版社，2009．

[12]楼少敏,王永达,许沧粟.基于路面不平度自功率谱密度函数计算国际不平度指数的研究[J]. 公路交通科技,2007(8):12-15.

[13]裴玉龙.道路交通安全[M].北京：人民交通出版社，2004.

中图法分类号：U491.1

doi:10.3963/j.issn.2095-3844.2015.01.031

收稿日期：2014-10-15

Transverse Rumble Strips Design And Comfort Evaluation
at Arterial Highway Unsignalized Intersection

YU Jinlin XU Liangjie LIU Qiyuan QIN Yaxiao

(SchoolofTransportation,WuhanUniversityofTechnology,Wuhan430063,China)

Abstract：To reduce the traffic accidents caused by driver’s speeding behavior,this paper sets transverse rumble strips at the functional area of intersection,and discuss its’ parameters design method.After that, we use improved weighted acceleration RMS and K coefficient method to establish the drivers’ comfort model by vibration frequency/amplitude/speed change.At last,we design some cases which are different from each other by deceleration and group, analyse drivers’ comfort and use it to optimize the transverse rumble strips design

Key words：trunk highway;unsignalized intersection;transverse rumble strips;vibration frequency;vibration comfort

*国家自然科学基金项目资助(批准号：51108362)