红灯倒计时对首车启动延误的影响*

杨京帅　孙正一　王文亮　杨得婷　苏　薇

(长安大学汽车学院　西安　710064)

红灯倒计时对首车启动延误的影响*

杨京帅孙正一王文亮杨得婷苏薇

(长安大学汽车学院西安710064)

摘要：针对红灯倒计时对首车启动延误的影响问题，选择具有代表性的4个路口作为观测地点，通过对观测者的培训与数据筛选，获得了600个可信度较高的首车启动延误数据.非参数检验分别得到驾驶员在有无红灯倒计，以及左转和直行情况下首车启动延误的差异.检验结果表明有无红灯倒计时对首车启动延误有显著影响(p=1.83×10-5)；左转和直行首车在有红灯倒计时的情况下差异显著(p=0.01)，在无红灯倒计时差异不显著(p=0.82)；直行首车启动延误在有无红灯倒计时情况下差异显著(p=8.86×10-6)，左转首车启动延误在有无红灯倒计时情况下差异不显著(p=0.11).

关键词：交通工程；红灯倒计时；非参数检验；道路交叉口；启动延误；驾驶行为

杨京帅(1978- )：男，工学博士，副教授，主要研究领域为道路交通安全、交通运输规划与管理

0引言

为使驾驶员在接近路口时更容易地判断是否提前制动或者通过路口，也为缓解驾驶员在等待放行前的焦躁，世界上很多国家在路口安装了绿灯倒计时设备和红灯倒计时设备，以期为驾驶员在路口处提供更多、更有效的信息[1-2].倒计时信号设备的普及引来诸多争议，Y.C.Chiou等[3]认为在安装红灯倒计时设备后的四五个月时间内，有效降低了启动延误以及饱和车流状态下的车头时距和总体排队车队启动延误.M.R.Ibrahim等[4]对比了3组有倒计时和无倒计时交叉口，研究显示倒计时设备降低了前6辆车的车头时距.T.Limanond等[5]将倒计时设备节约的启动延误时间折算为每小时可增加8～24辆车辆通过路口.K.M.Lum等[6]发现倒计时信号灯路口安装后的1.5个月，闯红灯现象减少了65%，但是随着时间的推移，闯红灯违章将恢复到倒计时信号灯安装前的水平.王岩、钱红波等[7-8]的研究表明，红灯倒计时会使驾驶员产生期待感和竞争感，这将导致部分驾驶员在放行前就抢先起步，这在降低启动延误的同时增加了发生交通事故的概率，建议谨慎采用倒计时设备.

本文选取2个有倒计时设备和2个没有倒计时设备的共4个两相位信号控制路口进行实地观测，4个观测路口均为平面十字交叉，车道分布、行人与非机动车的干扰等条件较为相似.在观测前对调研人员进行启动时间校准培训，以便尽可能准确地得到每次放行时刻每辆首车的启动时间，然后将筛选后得到的600个数据进行非参数检验分析.经过严格的数据采集、异常数据剔除、统计分析后，探讨红灯倒计时设备对首车启动延误的影响，左转与直行车辆启动延误的差异及其产生的原因.

1数据采集

1.1路口选择

本文在记录首车启动延误时基于如下定义：“自绿灯亮起时刻开始，到车辆有明显前移迹象为止.若车辆在绿灯亮起前启动，则启动延误为负值，即自车辆明显前移开始，到绿灯亮起时刻为止.”各路口交通状况见表1.

表1　调查路口交通状况

注：“东→西，西→东”表示记录了2个相向车道的首车启动延误；“南→西”表示记录了1个车道的首车启动延误.下同.

1.2调研人员培训

为确保数据采集的可信度，调研人员首先各自独立记录同一车道连续50个信号周期的首车启动延误数据，然后进行对比，偏差较大的调研人员及时更正采样口径，反复多次记录后将平均误差控制在5%以内，最后进行实际观测，并对较大值进行备注(如违章机动车或非机动车阻挡，特种车辆干扰，上一信号周期未清空车辆阻挡，驾驶员聊天，驾驶员操作失误等)，以备后期筛选.

1.3数据筛选

实际观测结束后对记录数据进行筛选.在此过程中剔除了D路口由西向北的一组数据，由于计算后发现该车道首车延误时间平均值为其他2个车道首车延误时间平均值的2倍.经实地再次观测发现，由西向北的车辆驾驶员视野与其他2个车道相比更狭小，这导致了启动延误的大幅增加.另外对于违章车辆或行人阻挡，急救车先行等因素引起的首车启动时间超过6 s的数据进行了谨慎的剔除.

1.4确定样本量

根据中心极限定理及其相关推论[9]，简单随机抽样确定样本量n的公式为：

(1)

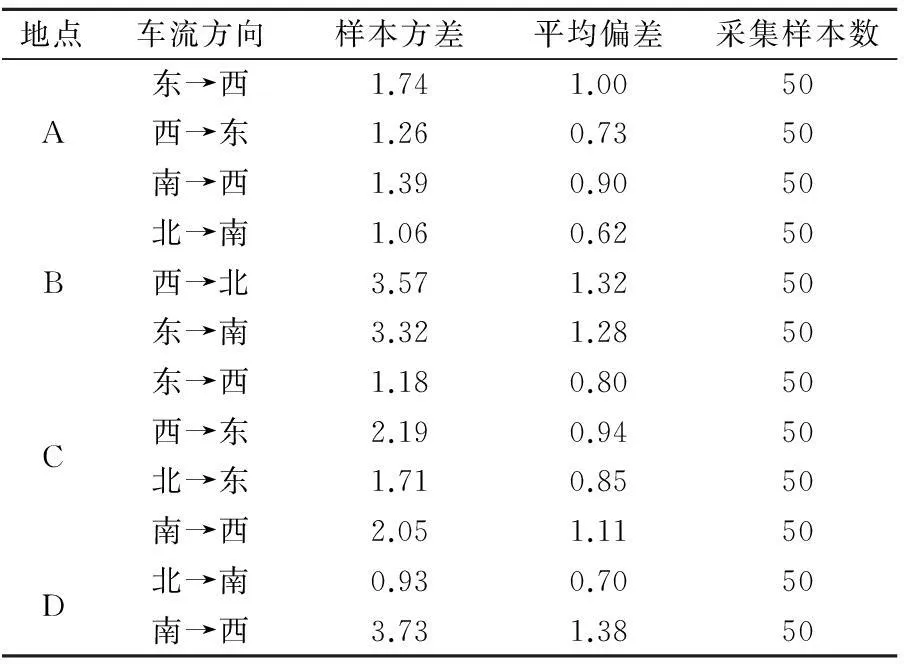
表2　路口各流向采样数

2数据分析

数据是信息的载体，分析数据中包含的主要信息须通过分析数据特征来实现，数据特征的分析内容包括数据的集中位置、离散程度等.各路口首车启动延误数据分析见表3.

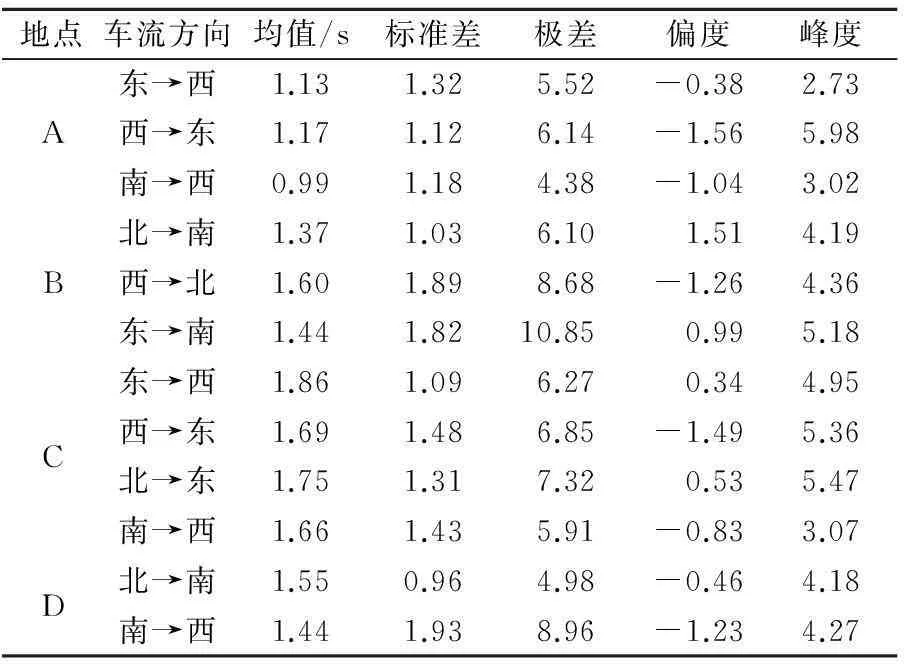
表3　各路口首车启动延误数据

偏度S是对概率密度函数对称性的度量.若S>0，则该分布是右偏的；若S<0，则该分布是左偏的.偏度值不仅表示偏斜的程度还表示偏斜的方向.峰度K是对概率密度函数“胖瘦”的度量，一般以标准正态分布的峰度值K=3为基准，如果K>3，表示该分布具有尖峰、粗尾的特征；如果K<3，表示该分布具有低峰、细尾的特征.

定义如下检验统计量.

(2)

Jarque和Bera证明了正态性假设

(3)

式(2)给出的TJB统计量渐近地服从自由度为2的χ2分布，用符号表示为

(4)

从式(2)可以看出，如果变量服从正态分布，则S=0，K=3，因而TJB统计量的值为0.但如果变量不是正态变量，则TJB统计量将随样本量逐渐增大.在某一显著水平下，根据式(2)计算的值超过临界的χ2值，则将拒绝正态分布的零假设H0；但如果没有超过临界的χ2值，则接受零假设H0.

利用MATLAB中的h=jbtest(x)语句，即Jarque-Bera法在置信度95%的水平下检验总体样本的正态性[10]，h=1，不服从正态分布.

由于真命题“有限个正态分布的线性组合仍然是正态分布”的逆否命题“(子样本线性组合构成的)总体样本不是正态分布，则这些子样本不全是正态分布”也为真，所以在对其子样本进行差异显著性研究时不能用方差分析法，而应用非参数分析法.

3差异显著性分析

非参数分析的宗旨是为了在不假定总体分布的情况下，尽量从数据本身来获得所需要的信息.本文应用非参数检验中的Kolmogorov-Smirnov(K-S)检验来研究差异的显著性[11].

3.1K-S检验

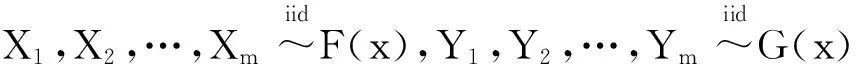
(5)

由Glivenko定理知，用经验分布函数来近似理论分布函数是可行的，于是Smirnov用统计量：

(6)

来检验上述假设问题，其中:F(x)和G(x)分别为X样本和Y样本的经验分布函数，X(i)和Y(j)分别为X样本和Y样本的顺序统计量，m,n为样本数；H0的拒绝域为某置信水平下显著性的最大值.统计量D所对应的显著性p由可靠性分布函数QK-S表示：

(7)

其中:

若两独立样本相似，统计量D→0，则P→1，反之亦然.取拒绝域为0.05，若显著性p>0.05，则认为两样本差异不显著；若显著性p<0.05，则认为两样本差异显著.

3.2样本检验与分析

3.2.1总体差异性

首先研究有红灯倒计时和无红灯倒计时两种情况下首车启动延误的差异性.经Jarque-Bera法验证，首车启动延误在有红灯倒计时和无红灯倒计时两种情况下，以95%的置信水平不服从正态分布.将有红灯倒计时和无红灯倒计时2种情况下首车启动延误数据分别记为样本1和样本2，经双样本K-S在95%的置信水平下检验得到有红灯倒计时和无红灯倒计时2种情况下首车启动延误的影响，如表4所示，其中K-SZ值含义即为式(6)中的统计量D，下同.

表4　有无红灯倒计时对首车启动延误的影响

有红灯倒计时和无红灯倒计时2种情况下，首车启动延误具有明显的显著性(p=1.83×10-5).有红灯倒计时的路口较无红灯倒计时的路口显著降低了首车启动延误，这是倒计时信号灯逐步推广的原因之一.倒计时信号灯路口显著降低了首车启动延误的可能原因是倒计时信号灯为路口的所有交通参与者提供了足够的准备时间，各交通参与者行为预期与步调基本一致，交叉口内车辆、行人和骑行者清空较完全，绿灯放行时驾驶员能快速启动车辆通过交叉口，启动延误降低.

3.2.2直行与左转首车启动延误的差异性

倒计时信号灯显著降低了首车启动延误，为了进一步分析同一种信号控制方式下，不同通行方向的首车启动延误是否具有差异性，对直行和左转的首车启动延误进行了观测.排除右转通行车辆的原因在于右转车辆不受信号灯的控制.左转和直行首车启动延误差异显著性分析见表5.

表5　直行和左转首车启动延误差异

在倒计时信号灯控制方式下，左转车辆与直行车辆首车启动延误具有显著性差异(p=0.01).左转车辆与对向直行车辆之间存在博弈，一个有趣的现象就是左转车辆与直行车辆谁先到达冲突点，晚到达冲突点的通行车辆，并不急于启动车辆，而是等待合适的穿越间隙通过路口.左转通行车辆体现的尤为明显，左转车辆通常采用不同的行驶轨迹，以求改变冲突点的位置，从而能够先行通过路口或寻找合适的穿越间隙通过路口.在A路口，左转首车的启动延误均值低于直行车辆，在B路口，左转首车的启动延误均值高于直行车辆，均是由于先行与后行到达冲突点这一原因造成的，或者说倒计时信号灯路口的空间形态造成了左转与直行首车启动延误的显著性差异.

在无倒计时信号灯控制方式下，左转车辆与直行车辆首车启动延误没有显著性差异(p>0.05).造成差异不显著的原因在于无红灯倒计时情况下，无论是直行车辆还是左转车辆，都没有足够的准备时间和心理预期.另一方面，无倒计时路口在某一方向刚放行时刻另一方向易产生上一信号相位未清空的车辆，或者行人、骑行者误以为能通过路口而使他们与刚放行车辆产生冲突，这都影响了直行和左转车辆的启动时间.以上均是造成左转和直行首车启动延误在有红灯倒计时情况下差异显著而在无红灯倒计时情况下差异不显著的原因.

倒计时与非倒计时路口数据汇总结果显示，左转和直行的首车启动延误差异不显著(p>0.05).左转和直行在无红灯倒计时的情况下受未清空车辆和行人的干预较大，以至于统计量综合后削弱了整体的显著程度.

3.2.3同一通行方向不同控制方式的差异性

左转与直行首车在倒计时信号控制方式下具有显著差异性，同一通行方向不同控制方式下首车启动延误是否同样具有差异性，为了检验这一差异，对左转车辆和直行车辆在有无红灯倒计时两种情况下的差异性进行检验(见表6).

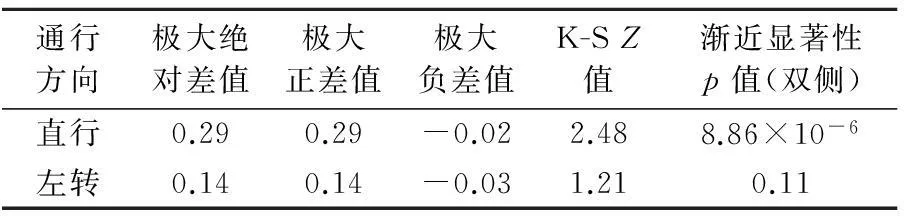
表6　有无红灯倒计时直行与左转首车启动延误差异

直行首车启动延误在有红灯倒计时和无红灯倒计时2种情况下具有显著性差异(p=8.86×10-6)，红灯倒计时较无红灯倒计时显著降低了直行方向首车的启动延误.但是左转首车在有红灯倒计时和无红灯倒计时两种情况下并没有体现出显著性差异(p=0.11).造成这一差异的原因，可能是左转车辆相比直行车辆在通过路口的过程中具有更多的冲突点，驾驶操作相对困难[12]，感受到的风险相对较大[13]，倒计时信号灯并没有消除左转驾驶员的这种心理感受，直行驾驶员则不存在这种心理感受和相对困难的驾驶操作，所以有无红灯倒计时对直行首车启动延误影响显著，而对左转首车启动延误影响不显著.

4结束语

有无红灯倒计时对首车启动延误具有显著性差异；在倒计时信号灯控制方式下，直行车辆与左转车辆首车启动延误具有显著性差异，而在非倒计时信号灯控制路口，这种差异性并不显著；直行首车启动延误在有红灯倒计时和无红灯倒计时两种情况下具有显著性差异，左转首车在有红灯倒计时和无红灯倒计时两种情况下没有体现出显著性差异.

以上研究结论是基于两相位信号控制路口平峰时段的观测统计分析得出的，信号转换期间的路口清空较完全，以保证首车启动延误主要是受信号控制方式的影响.在路口流量较大，路口清空不完全，不同转向车辆与行人、骑行者之间相互干扰较大的情况下，倒计时信号控制能否显著降低首车启动延误需要进一步观测分析.

参 考 文 献

[1]PAPAIOANNOU P. Driver behaviour, dilemma zone and safety effects at urban signalised intersections in Greece [J]. Accident Analysis and Prevention, 2007, 39(1):147-158.

[2]LONG K J, LIU Y, HAN L D. Impact of countdown timer on driving maneuvers after the yellow onset at signalized intersections: An empirical study in Changsha, China[J]. Safety Science, 2013, 54(4): 8-16.

[3]CHIOU Y C, CHANG C H. Driver responses to green and red vehicular signal countdown displays: Safety and efficiency aspects [J]. Accident Analysis and Prevention, 2010, 42(4): 1057-1065.

[4]IBRAHIM M R, KARIM M R, KIDWAI F A. The effect of digital count-down display on signalized junction performance [J]. American Journal of Applied Science, 2008, 5(5): 479-482.

[5]LIMANOND T, CHOOKERD S, ROUBTONGLANG N. Effects of countdown timers on queue discharge characteristics of through movement at a signalized intersection [J]. Transportation Research Part C: Emerging Technologies, 2009, 17(6): 662-671.

[6]LUM K M, HALIM H. A before-and-after study on green signal countdown device installation [J]. Transportation Research Part F: Traffic Psychology and Behavior, 2006, 9(1): 29-41.

[7]王岩，杨晓光. 基于交通安全的交叉口倒计时信号灯设置研究[J]. 中国安全科学学报, 2006, 16(3): 55-59.

[8]钱红波, 韩皓. 机动车绿灯倒计时对交叉口交通安全的影响研究[J]. 中国安全科学学报, 2010, 20(3): 9-13.

[9]贾俊平, 何晓群, 金勇进. 统计学[M]. 北京: 中国人民大学出版社，2009.

[10]王岩, 隋思涟. 试验设计与MATLAB数据分析[M]. 北京: 清华大学出版社，2012.

[11]孙振绮, 丁效华. 概率论与数理统计[M]. 北京: 机械工业出版社，2012.

[12]GSTALTER H, FASTENMEIER W. Reliability of drivers in urban intersections [J]. Accident Analysis and Prevention, 2010, 42(1): 225-234.

[13]SLOVIC P, PETERS E. Risk perception and affect [J]. Current Directions in Psychological Science, 2006, 15 (6): 322-325.

中图法分类号：U491

doi:10.3963/j.issn.2095-3844.2015.01.005

收稿日期：2014-05-19

Influence of Red Signal Countdown Display
on the First Vehicle Start-up Delay

YANG JingshuaiSUN ZhengyiWANG WenliangYANG DetingSU Wei

(SchoolofAutomobile,Chang’anUniversity,Xi’an710064,China)

Abstract：To research the influence of red signal countdown display (RSCD) on the first vehicle start-up delay, 4 representative observation intersections were selected. By means of training observers and filtering data, 600 data of the first vehicle start-up delay with high credibility were acquired. The differences between the first vehicle start-up delay under situations of with-without RSCD, turning left and going straight were analyzed respectively by nonparametric test. The results indicated that there was significant difference for the first vehicle start-up delay between countdown and non-countdown signalized intersections (p=1.83×10-5). There was a significant difference between the first vehicle start-up delay of turning left and going straight at intersections with RSCD (p=0.01), but non-significant difference at intersections without RSCD (p=0.82). There was a significant difference for the first vehicle start-up delay of going straight under situations of with-without RSCD (p=8.86×10-6), but non-significant difference for the first vehicle start-up delay of turning left with-without RSCD (p=0.11).

Key words：traffic engineering；red signal countdown display；nonparametric test；road intersection；start-up delay；driving behavior

*国家自然科学基金项目(批准号：51108040)、中央高校基本科研业务费专项资料项目(批准号：CHD2011JC105)资助