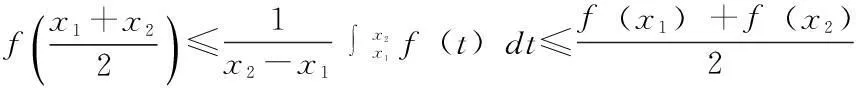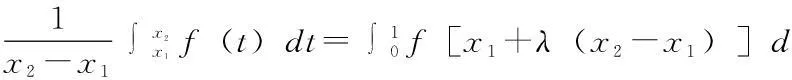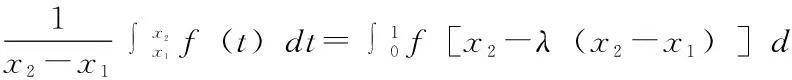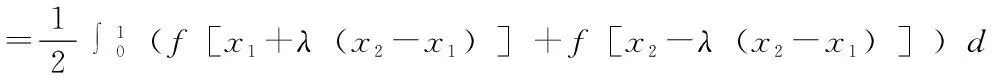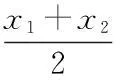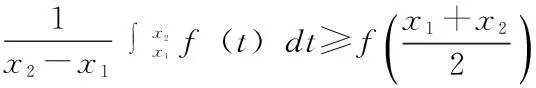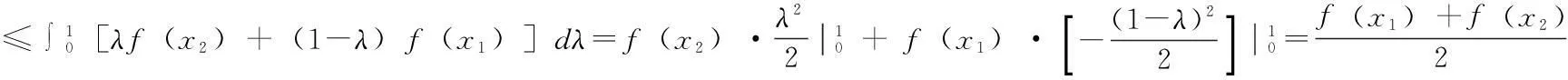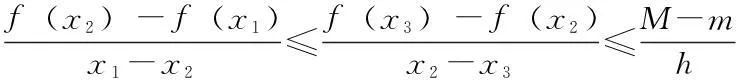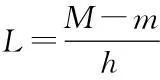凸函数的性质及应用

文/程双青

摘　要：凸函数是大学数学中一重要的概念,在其他学科中应用比较多,本文主要研究凸函数的性质及性质的一些应用.

关键词：凸函数;性质;应用

凸函数的性质及应用

文/程双青

摘要：凸函数是大学数学中一重要的概念,在其他学科中应用比较多,本文主要研究凸函数的性质及性质的一些应用.

关键词：凸函数;性质;应用

作者简介：程双青,硕士,西安汽车科技职业学院。

中图分类号：G632

文献标志码：码：A

文章编号：号：2095-9214(2015)08-0180-01

1.凸函数的性质

文[1]给出了如下的两定理:

定理1.1设f(x)在区间[a,b]上定义,f(x)是凸函数充分必要条件为：∀x1,x2,x3∈[a,b],x1

(1.1)

定理1.2设f(x)在区间[a,b]上定义,且在(a,b)上可导,则f(x)是凸函数的充分必要条件是：∀x0∈(a,b)有

f(x)≥f(x0)+f′(x0)(x-x0)(a≤x≤b)

(1.2)

定理1.3 对R上连续的凸函数g(x),存在R上的实值非降函数h(x),使得对任意的x,y∈R,成立不等式：

g(y)-g(x)≥h(x)(y-x)

(1.3)

比较(1.2)、(1.3),从而得出凸函数的一等价性质.

定理1.4设f(x)在区间[a,b]上有定义,则f(x)是凸函数的充分必要条件为：存在(a,b)上定义的函数h(x),使得∀x0∈(a,b)有

f(x)≥f(x0)+h(x0)(x-x0)x∈[a,b]

2.凸函数的应用

例1设f(x)是[a,b]上连续的凸函数,试证：∀x1,x2∈[a,b],x1

证明 令t=x1+λ(x2-x1),λ∈(0,1),则

(2.1)

同理,令t=x2-λ(x2-x1),亦有

从而

(2.2)

故由(2.2)得

另外,由(3.1),应用f(x)的凸性,

例2设f(x)为区间(a,b)内的凸函数,试证：f(x)在(a,b)的任一闭区间[α,β]⊂(a,b)上满足Lipschitz条件.

证明 要证明f(x)在区间[α,β]上满足Lipschitz条件,即要证明：∃L>0,使得∀x1,x2∈[α,β]有

因为[α,β]⊂(a,b),故可取h>0充分小,使得[α-h,β+h]⊂(a,b)于是∀x1,x2∈[α,β],若x1

其中M,m分别表示f(x)在[α-h,β+h]上的上下界,从而

(*)

若x2

由此亦可推得(*)成立.

(作者单位：西安汽车科技职业学院)

参考文献：

[1]企方勤编,数学分析(上)[M].北京:高等教育出版社.1986.132—133.

[2]裴礼文编.数学分析中的经典问题与方法[M]].北京:高等教育出版社.2006.269—270.

[3]华东师范大学数学系编.数学分析(上)[M].北京:高等教育出版社.2001.148—149.

[4]丁晓庆编.工科数学分析[M].北京:科学出版社.2007.202-210.

[5]刘三阳,于力,李广民编.数学分析选讲[M].北京:科学出版社.2007.77—89.

[6]赵海清.刘瑞元编.有关凸函数的一个定理改进证明.纯数函数与应用数学[J].2004.386—388.