一种模型预测控制算法在国产DP系统中的应用

一种模型预测控制算法在国产DP系统中的应用

韩冰,董胜利

(上海船舶运输科学研究所 航运技术与安全国家重点实验室， 上海 200135)

摘要:在动力定位系统对风和流的作用力进行前馈控制的基础上，将卡尔曼滤波的状态估计方法运用于估算船舶低频运动信号，提出一种基于专家经验的模型预测控制算法。为检验该算法的控制精度和控制稳定性等技术指标，结合目标船的实际情况，对动力定位系统的水池试验进行了设计。不同模拟环境下的试验结果表明，该控制算法能够满足目标船对动力定位控制系统的技术要求，具有良好的控制精度和稳定性。

关键词:动力定位系统； 卡尔曼滤波； 模型预测控制； 专家控制

收稿日期：2015-01-11

基金项目：上海市青年科技启明星计划资助(15QB1400800)

作者简介：韩冰(1981—)，男，吉林省吉林市人，副研究员，博士，硕士生导师，从事船舶动力装置仿真及动力定位控制系统研究。

文章编号：1674-5949(2015)02-001-07

中图分类号：U664.82文献标志码：A

An Model Predictive Control Algorithm and its Application in a

Dynamic Positioning System

HanBing，DongShengli

(Shanghai Ship and Shipping Research Institute, State Key Laboratory of

Navigation and Safety Technology, Shanghai 200135, China)

Abstract:An expert experience model predictive control strategy is introduced into the feed-forward control of wind and current and the Kalman filter for the low frequency motion estimation in the dynamic positioning system. For examining the control accuracy and control stability of the strategy, a pool test of the dynamic positioning system is designed and completed based on the actual situation of the target ship. The test results in different simulated environments show that the control strategy of the dynamic positioning system meets the technical requirements of the target ship with good control accuracy and stability.

Key words: dynamic positioning system; Kalman filter; model predictive control; expert control

0引言

动力定位系统(Dynamic Positioning System)是一种闭环的控制系统[1-2]，能够不借助锚泊系统的作用，不断检测出船舶的实际位置与目标位置的偏差，再根据风、浪、流等外界环境力的影响计算出使船舶恢复到目标位置所需的推力，并对船舶上各推力器进行推力分配，进而使各推力器产生相应的推力，使船舶保持在所要求的位置上。其优点是定位成本不会随水深的增加而增加，操作也比较方便。

自20世纪60年代早期动力定位系统产生以来，PID(Proportion Integration Differentiation)控制在船舶位置的控制方面得到了较多的应用[3]。PID控制器可分别对船舶在海平面内纵荡、横荡及艏摇3个自由度上的运动实施控制，但控制效果一直受到船舶运动耦合及控制相位滞后所带来问题的影响。Balchen等[4]提出了一种以现代控制理论为基础的控制技术——最优控制与卡尔曼滤波理论相结合的动力定位控制方法，即第二代也是应用比较广泛的动力定位系统。卡尔曼滤波在这里的主要作用是测量所得到的船舶综合运动信息，估计其低频运动状态并反馈给控制器，构成针对船舶低频运动的线性最优(Linear Quadratic Gaussian, LQG)控制。在对动力定位控制系统进行不断深入研究的过程中，H∞控制理论和鲁棒控制也被逐步应用其中，并在一定程度上解决了LQG控制模型不精确所带来的问题。随着智能控制理论不断丰富和发展，以模糊逻辑、专家系统、神经网络为代表的智能控制方法近年来也被应用到了动力定位系统的控制中。此外，随着我国对海洋资源开发日益重视，动力定位系统的研发在国内也已得到广泛重视。哈尔滨工程大学、上海交通大学等科研机构在动力定位系统的研究方面取得了一些理论研究成果[5-7]，这些研究成果为我国自主研发动力定位控制系统打下了良好的基础。

上海船舶运输科学研究所在已研制成功的SRI-VC2110船舶机舱自动化系列产品的基础上，研究开发出了SRI-VC2110DP系列动力定位控制系统，并将其应用到了该所自主设计的2 000 t起重船上。对于新型的动力定位控制系统产品，通常需要在实船安装前进行水池试验测试，以验证产品的功能、性能等技术指标。针对SRI-VC2110DP动力定位系统进行了水池试验设计，并通过动力定位水池试验模拟实船操作，对系统进行优化设计；在自适应模型预测控制方法的基础上，提出一种适用于动力定位控制的专家控制策略。通过进行各种自然海况条件下的模拟控制试验，验证系统的稳定性，同时分析系统的控制能力和控制精度。

1SRI-VC2110DP控制系统

动力定位控制系统的主要任务是根据船舶当前状态与目标状态的偏差对船位与艏向进行控制，并保持船舶运动状态。SRI-VC2110DP控制系统基于船舶运动模型的模型预测控制结构，通过自适应扩展卡尔曼滤波算法对船舶的运动状态进行分析估计，采用多种控制测量方式进行定位控制。整个预测控制系统由风力计算模块、流力估计模块、卡尔曼滤波状态估计器、控制器和推力分配模块等构成。控制系统的原理见图1。

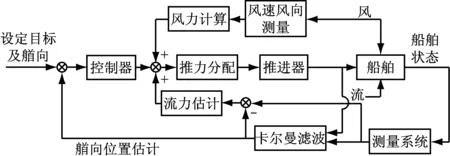
图1　动力定位控制系统的原理框图

动力定位控制系统中的控制器用来计算推力器应提供的力和力矩，以抵抗外界的干扰，使船舶保持在要求的位置。动力定位控制系统共有3个控制量，因此系统有3个控制回路，每个控制回路有单独的控制器。

1.1自适应船舶运动模型

建立船舶低频运动数学模型是研制动力定位控制系统的核心。对一般海洋工程船而言，SRI-VC2110DP控制系统可根据船舶在运动中的数据进行运动模型参数辨识，避免了复杂的工作。用于描述船舶运动的数学模型可分为低频运动模型和高频运动模型。低频运动模型用于描述船舶在水平面的运动，高频运动模型用于描述船舶受海浪等因素影响所产生的位置振荡。

对船舶运动的模型描述，在文献[4]中给出的一般性船舶高低频运动模型的基础上，分别建立船舶高低频运动模型，并在水池试验中利用卡尔曼滤波算法对模型参数进行实时修正。

1.2卡尔曼滤波估计

动力定位系统控制过程中，波频信号在船舶的运动中仅表现为周期性的振荡，不会改变船舶的平均位置。因此,为了在动力定位控制中避免不必要的能量浪费以及推力器的磨损，仅对低频运动加以控制。动力定位系统中的卡尔曼滤波器主要用于修正预测模型参数，并对测量信号中的高频信号进行滤波，得到低频运动信号。

假设船舶运动的综合模型可表示为

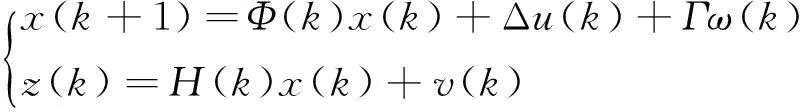
(1)

式(1)中：ω为过程噪声和模型不确定度；v为测量噪声；假设它们均服从高斯白噪声分布。

根据卡尔曼滤波算法，可对船舶运动方程做以下滤波计算。

系统初始化：

(2)

(3)

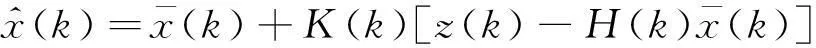
(4)

(5)

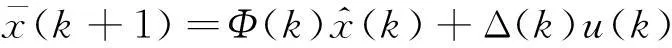
(6)

(7)

k=k+1时，返回式(2)

根据以上方程，对船舶平面运动模型速度变量进行滤波仿真。

1.3风力和流力的计算

船舶在海上作业时会受到环境的干扰，使船位和艏向发生变化。一般环境力是指海上风、浪、流等对船的作用力。风对船的作用力可采用模型进行计算。由于波浪对船的漂移力相对流作用力较小，因此在实际控制中可忽略。海流对船的作用力通常需要根据船舶运动状态进行估计计算。

1.3.1风力计算

设ρ0为空气密度(计算取0.132 26 kg×s2/m4)，则风力(矩)可表达为

(8)

式(8)中：Ax为上层建筑正投影面积；Ay为上层建筑侧投影面积；L1为船舶总长；Cwx，Cwy，Cwm分别为纵向、横向风力及风力矩系数。

1.3.2流力模型

海流对船舶作用的时变性较弱，因此可通过预测模型状态与实际船舶运动状态测量值之间的偏差进行海流估计。采用这种计算方法的同时，可以将风、流以外的扰动一同进行补偿计算。

1.4基于专家知识的控制器设计

动力定位控制系统的控制策略是:将通过位置测量系统所得到的实际状态信号与预定目标值比较，计算抵消位置偏差和外接干扰所需的推力大小，经推力分配，对推进器发出控制指令以实现船舶的定位控制。PID控制器是一种线性控制器，根据给定值与实际输出值构成控制偏差e(t)。其控制规律为

(9)

写成传递函数形式，则有

(10)

式(9)~式(10)中：kp为控制系统增益。

目前实际应用的动力定位系统大都采用带有固定参数的PID控制算法。考虑到天气和船速突变等特殊状况对控制系统的影响，需在应用PID控制器的同时引入高频滤波器，以保证控制器的稳定。但因实际船舶运动惯性较大，采用常规PID控制算法容易出现船舶振荡、稳定时间长等情况。对于惯性较大的船舶控制对象，针对船舶在动力定位过程中的不同运动状态采用不同的控制策略往往是比较有效的方法。在进行大量水池试验的基础上，提出一种适用于动力定位系统的专家控制策略，以解决船舶定位控制过程中的振荡问题。

令e(k)为离散采用时刻的控制误差，e(k-1)和e(k-2)分别为前1个和前2个时刻的控制误差，则有

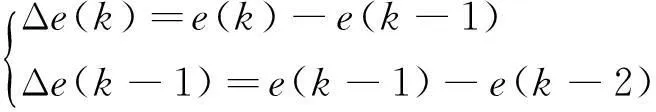
(11)

根据动力定位船与目标位置的偏差关系，专家控制策略可分为以下5种情况设计。

(2) 当e(k)Δe(k)>0时，船舶在朝偏离目标位置运动，这时应增大控制增益，改变船舶的运动趋势;

(3) 当e(k)Δe(k)<0，e(k)e(k-1)>0时，船舶在朝控制目标靠近，这时应减小控制增益，防止产生较大的超调量;

(4) 当e(k)Δe(k)>0,e(k)e(k-1)<0时，船舶处于运动方向转换位置，这时控制器输出保持上一时刻的作用;

2动力定位水池试验系统设计

2.1SRI-VC2110DP动力定位系统

SRI-VC2110DP系列船舶动力定位系统按我国船级社规范与德国劳氏船级社规范设计,由动力定位操纵台、推力器操纵台、侧翼操纵终端、控制箱、打印机及各种传感器组成。整个系列包括3种满足规范要求的附加标志产品，即DP-1、DP-2及DP-3。SRI-VC2110DP1是基本型的动力定位控制系统(见图2)。

SRI-VC2110DP系统的基本组成为：动力定位操纵台、推力器遥控操作台、侧翼操作板、侧翼接线盒、联合操纵终端、控制箱、测量系统传感器、UPS不间断电源以及报警事件记录打印机等。设备的数量根据规范附加标志DP-1、DP-2及DP-3的要求而定。

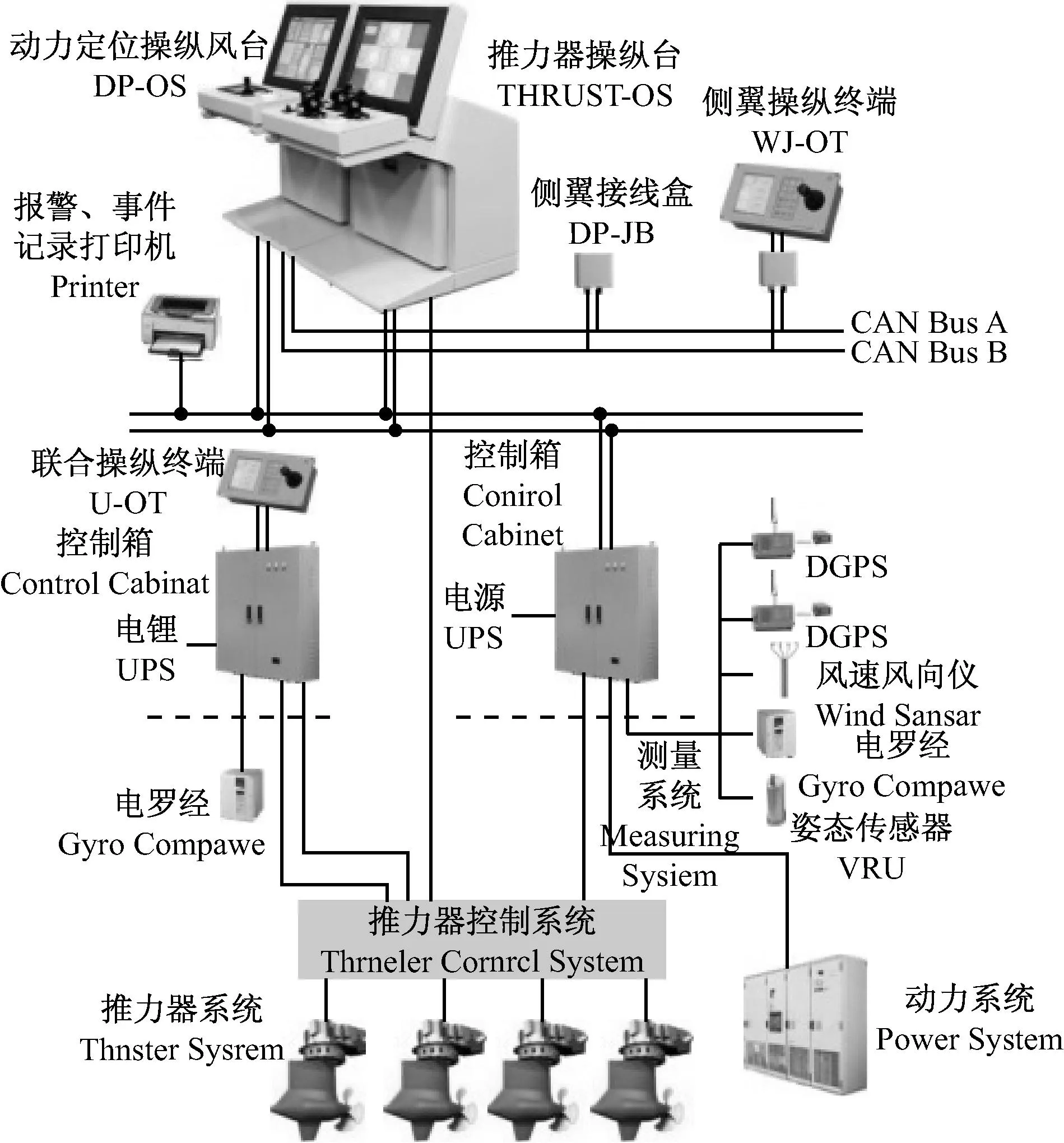
图2　SRI-VC2110DP1系统组成框图

2.2水池试验系统设计

为检验所提出的控制算法在动力定位控制中的控制能力，对SRI-VC2110DP系统的水池试验系统进行了设计。用于水池试验的试验系统主要由动力定位系统操纵台、控制计算机和数据记录计算机组成，通过以太网组成通信网络。试验过程中控制参数的设置、船模及环境状态的显示通过动力定位操纵台的人机界面完成。船模的目标位置、控制模式、增益选择、推力器使能等信息可通过操纵台控制面板上的触摸按钮发送到控制箱中的控制计算机。控制计算机根据目标位置、船模当前状态以及船模所处环境信息，计算出完成当前控制任务的推力和转矩，并运用推力分配算法完成每个推进器推力大小和方位的计算。此外，控制箱中还包含多个不同种类的通信模块，除将控制命令发送到各推进器外，主要用于传感器的数据采集和转换。系统中的数据记录仪用于实时记录系统中全部测点数据，并根据需要在试验过程中动态显示关键参数的动态变化曲线。试验系统示意图见图3，试验环境见图4。

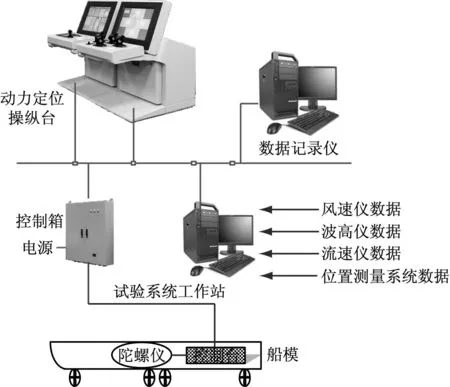
图3　SRI-VC2110DP1水池试验系统组成框图

图4　水池试验系统

2.3试验模型及其推进装置

水池试验控制对象是振华重工(集团)股份有限公司承建的2 000 t全回转起重船。该船为无螺旋桨推进的非自航浅吃水起重船，艏艉各配置1套1 500 kW的全回转Z型导管推力器，其与布置在舯部两舷的同功率推力器一起组成推力系统。试验按λ=28的缩尺比建造水池试验模型，根据缩尺比设计的船模的主要参数见表1。

船模的螺旋桨按缩尺比线性关系根据实船船桨设计，分别由可编程逻辑控制器控制的推进电机和方位角电机驱动。模型桨推力按缩尺比的三次方关系计算，扭矩按缩尺比的四次方关系计算，转速按缩尺比平方根的倒数关系计算。模型桨与实船桨尺寸见表2。

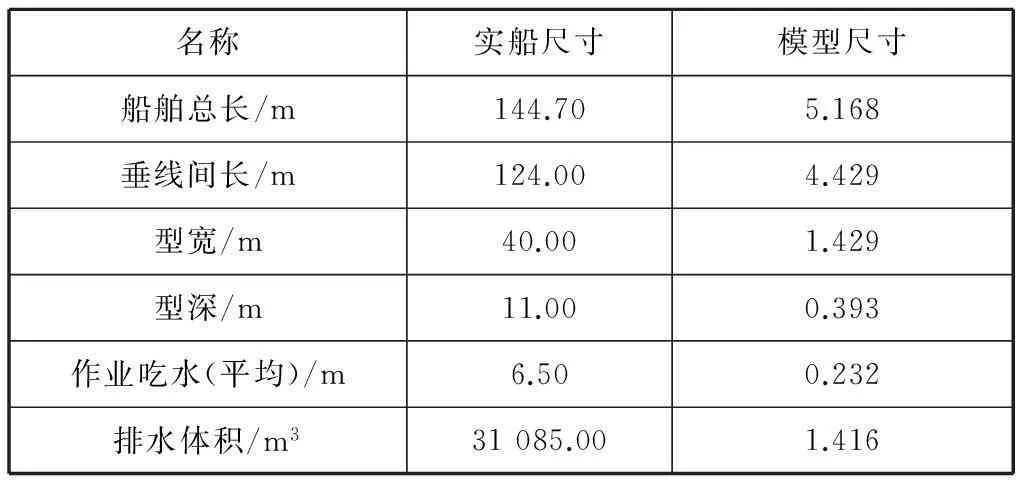
表1　船模主要参数表

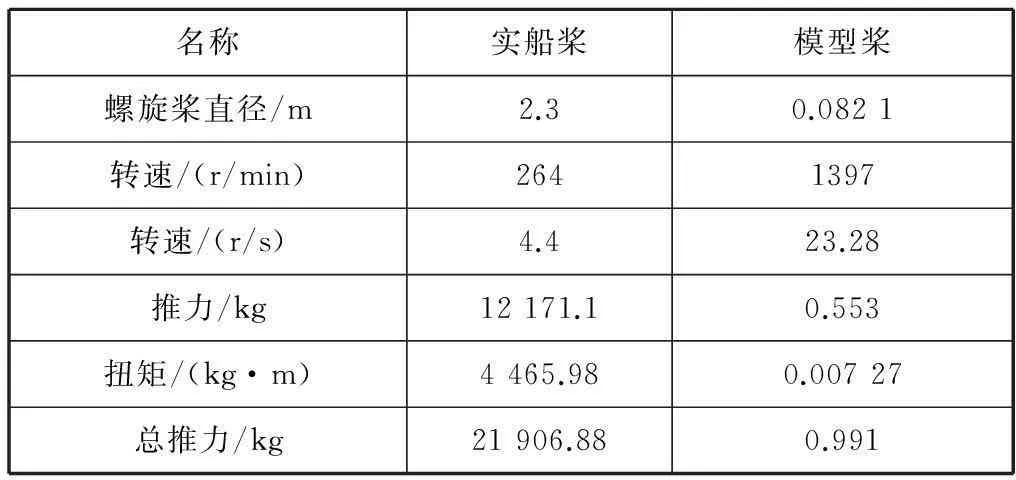
表2　船桨模型主要参数表

此外，为模拟风力对船模的作用情况，船模按比例装配了上层建筑模型和起重机模型,船模动力系统由岸上电缆配电,动力定位控制系统通过以太网与船模动力控制箱连接。

2.4传感器及测量装置

涉及的各项试验均在航运技术与安全国家重点实验室提供的风浪流水池中进行。试验测量装置分为环境测量装置、船模运动测量装置和推进器状态监测装置,其中环境测量装置主要包括声学多普勒流速仪、热线风速变送器、非接触伺服式浪高仪和电容式浪高仪，主要用于试验过程中对风、浪、流的测量。

船模运动测量装置有姿态和航向参考系统(Attitude and Heading Reference System，AHRS)和摄像位置采集装置。AHRS安装在船舶重心位置，用于测量船模艏向和摇摆姿态。由于AHRS在试验环境中容易受到环境磁场的干扰，因此实际应用过程中会发生测量参数跳变，测量误差范围约为±2°。用于测量船模位置的摄像装置采用无接触的光学测量和光源跟踪方式，通过计算机图像处理程序将视频采集信号转换为光源位置坐标，实现船模位置测量。位置测量系统测量精度约为0.02 m。

3水池试验验证

为验证所提出的专家经验控制方法在真实海况下的控制效果，通过水池模拟风、浪、流环境条件，进行船舶动力定位控制试验。分别对船舶有利艏向和非有利艏向2种情况进行试验，以比较所提出的控制方法和传统控制方法在定位控制中的效果。试验以目标船作业条件为依据设置水池试验环境(见表3)。

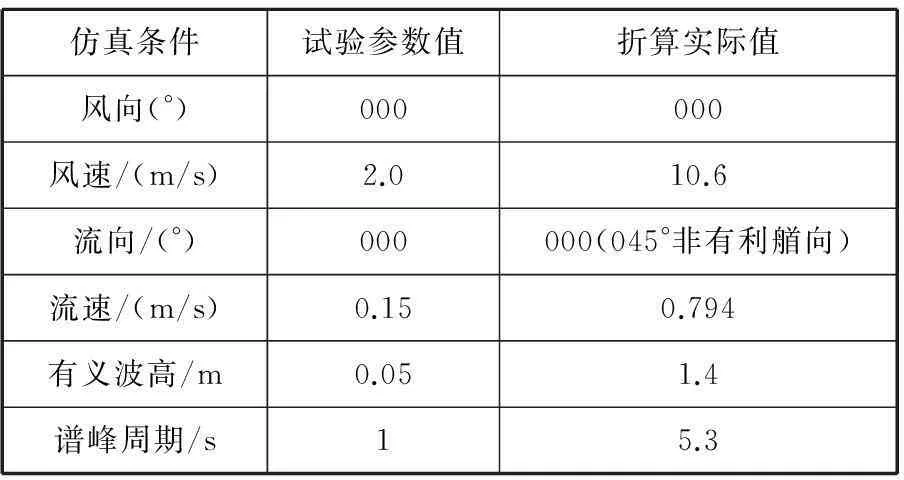
表3　水池试验条件参数表

3.1最优艏向条件下的定位控制试验

试验过程中的流向和风向均为000°，船舶定位设置成有利艏向条件下的自动定位控制。采用所提出的基于专家经验的控制方法得到的船舶定位曲线见图5，定位过程中船舶艏向变化曲线见图6。

从图5给出的船舶运动轨迹可以看出，所提出的控制算法能有效控制船舶的位置，并能稳定控制在目标位置区域。位置控制均方误差<0.03 m，折合实际船舶位置误差<0.84 m。控制过程中艏向最大误差≤3°，艏向均方误差<0.8°，折合实际船舶控制误差<0.8°。

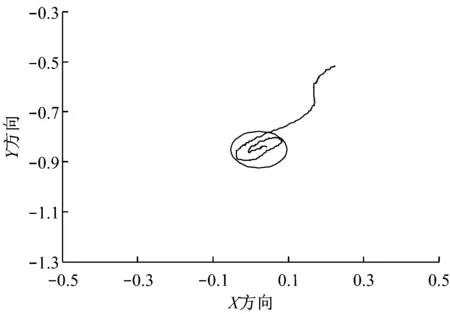
图5　船舶自动定位位置变化曲线

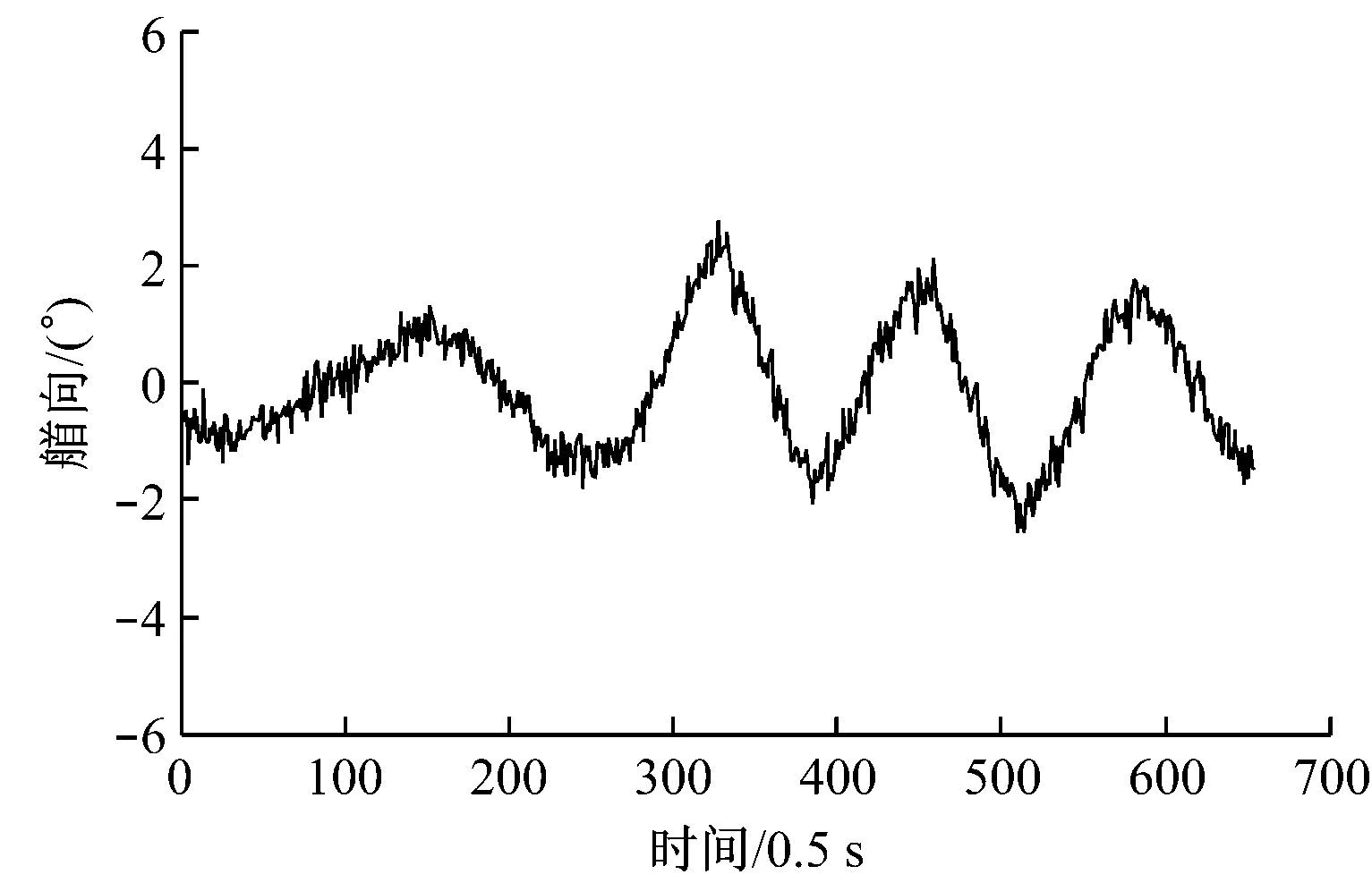
图6　船舶自动定位艏向变化曲线

在同样的环境力条件下，采用一般PID控制策略对船模进行定位控制试验，试验结果见图7和图8。从试验结果中可以看出，定位控制过程中船舶位置波动范围较大，船舶失踪处于较大范围的振荡。定位过程中，位置均方误差为0.11 m，折合实际船舶位置误差3.08 m；同时，控制过程中船舶艏向控制最大误差大约为4°，均方误差为1.89°。

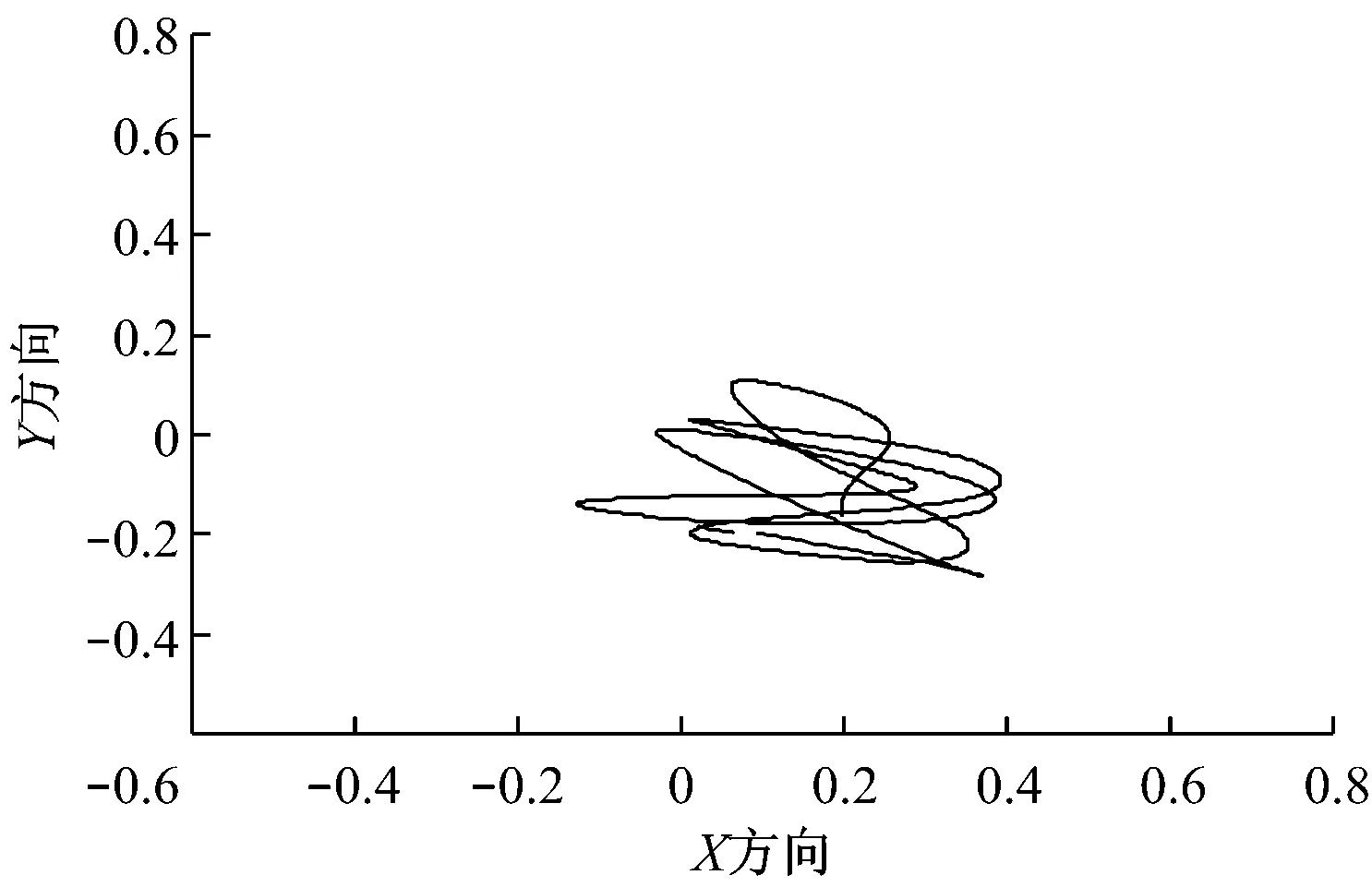
图7　PID控制船舶自动定位位置变化曲线

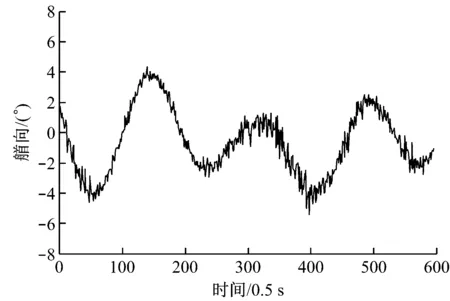
图8　PID控制船舶自动定位艏向变化曲线

3.2非最优艏向条件下的定位控制试验

试验过程中流向为045°，风向为000°，船舶定位控制为非有利艏向条件下的自动定位控制。采用提出的基于专家经验的控制方法得到的船舶定位曲线见图9，定位过程中船舶艏向变化曲线见图10。

从图9和图10中可以看出，在非有利艏向条件下，所提出的专家控制策略仍能对船舶位置进行有效控制，定位控制过程中最大误差≤0.1 m，均方误差为0.05 m，折合实际1.4 m。艏向最大误差≤3°，均方误差为1.1°，折合实际船舶均方误差为1.1°。

在非有利艏向条件下,采用一般PID控制方法的船舶运动轨迹和艏向分别见图11和图12。可见，虽然一般PID控制方法能够控制船舶位置，但船舶始终在目标位置附近振荡。与此同时，在非有利艏向条件下，船舶艏向振荡也比较明显。

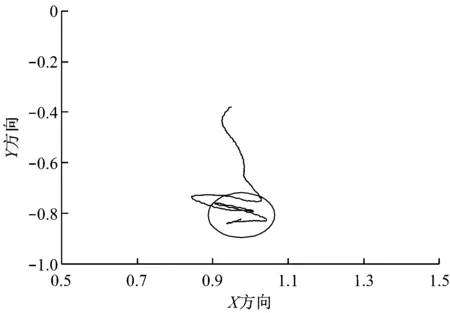
图9　船舶自动定位位置变化曲线

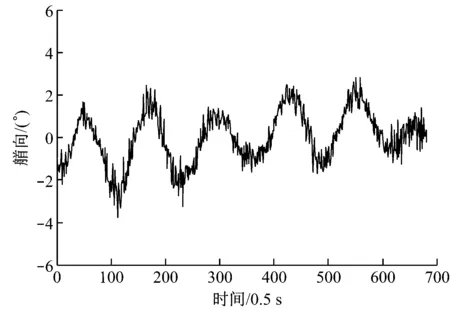
图10　船舶自动定位艏向变化曲线

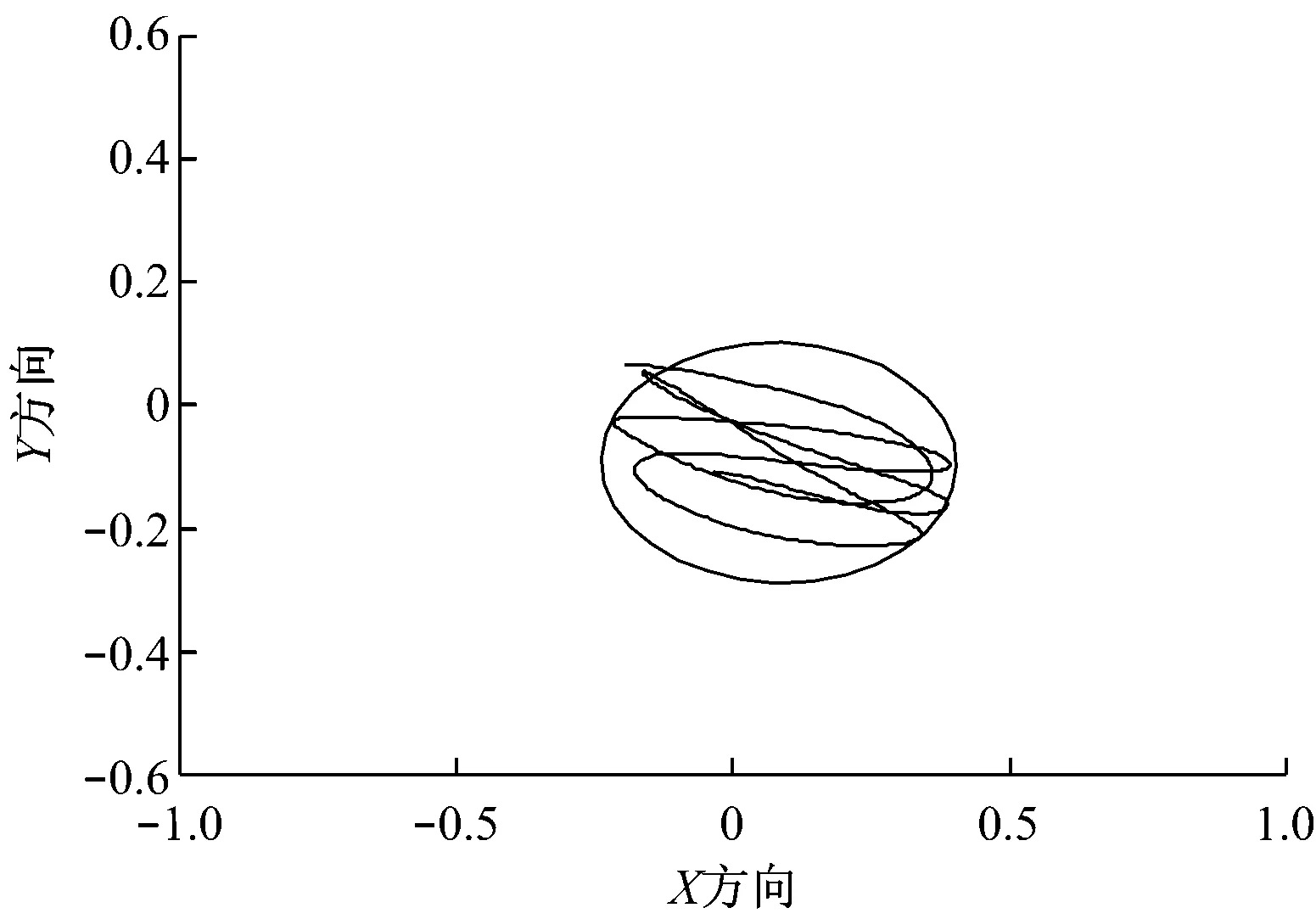
图11　PID控制船舶自动定位位置变化曲线

图12　PID控制船舶自动定位艏向变化曲线

从水池试验结果可以看出,采用提出控制策略的SRI-VC2110DP动力定位控制系统能够更有效地对船模进行控制。由于试验用于艏向测量的AHRS容易受磁场影响，干扰了艏向的测量，因此在控制过程中也影响了系统的控制精度。此外,水池试验系统船模的供电和通信通过有线方式完成，用于供电和通信的线缆由于自重和风力作用也会对试验结果产生较大影响，造成系统控制误差。如果试验条件得到改善，所提出的控制策略能够达到更高的控制精度。

4结语

针对SRI-VC2110DP动力定位系统对定位控制算法的需要，提出了一种基于专家知识的动力定位控制策略。该方法能够根据船舶在动力定位过程中的不同运动状态自适应选择不同的控制参数，有效避免大惯性被控对象所引起的系统振荡。为检验所提方法的工程实用性，设计了SRI-VC2110DP动力定位系统的水池试验系统。多项水池试验证明了所提控制策略的有效性，试验结果表明，所提出的控制方法的精度能够满足目标船对动力定位控制系统精度的要求。

参考文献：

[1]Selkainaho J. Tuning a Dynamic Positioning System [J]. Automatica, 1993, 29(4):865-875.

[2]赵志高,杨建民,王磊,等.动力定位系统发展状况及研究方法[J].海洋工程,2002, 20(1):91-97.

[3]Balchen J G, Jenssen N A, Saelid S. Dynamic Positioning Using Kalman Filtering and Optimal Control Theory[C]. IFACPIFIP Symposium on Automation in Offshore Oil Field Operation, 1976.

[4]Balchen J G, Jenssen N A, Mathisen E,etal. A Dynamic Positioning System Based on Kalman Filtering and Optimal Control[J]. Modeling, Identification and Control, 1980, 3(1):135-163.

[5]王元慧，施小成，边信黔. 基于模型预测控制的船舶动力定位约束控制[J]. 船舶工程，2007，29 (3):22-25.

[6]李文魁，张博，田蔚风,等.一种波浪中的船舶动力定位运动建模方法研究[J].仪器仪表学报，2007，28(6):1051-1054.

[7]童进军，何黎明，田作华. 船舶动力定位系统的数学模型[J]. 船舶工程,2002,24(5):27-29.

[8]童进军，何黎明，田作华. 船舶动力定位系统控制器的设计[J]. 船舶工程,2002,24(6):50-53.