空间观念深入途径：感受、感应、感悟

凌云志+汪辉

“空间与几何”被新课标列为十大核心概念之一.其“核心”意义至少有两个方面：从学科角度看，数学是研究空间形式和数量关系的科学.“空间与几何”作为数学三大领域之一，共同架构起数学知识体系，孕育思想方法.而空间观念又是学习这一领域的慧眼，为什么这么说？首先我们弄清什么是空间观念，简单地说就是对图形的数学看法和想法.它是发现与解决几何问题的数学思维先导.空间观念的品质决定解决几何问题的思维深度与广度.因而空间观念对学好数学具有“干细胞”意义；从教学反思角度看，学生很多解题缺陷都可溯源于“空间观念”某种图形观点或意识的缺失.因此，“空间观念”在学与教两个方面都处在“核心”地位.问题是我们怎样建立与发挥它的核心作用？

当下对“空间观念”的阐释，偏重于“能力”视角：（1）根据物体特征抽象出几何图形.反之，由几何图形想象出所描述的实际物体；（2）想象出物体的方位和相互之间位置关系；（3）描述图形的运动和变化；（4）依据语言的描述画出图形等.

对空间观念的培养途径，已有共识：（1）依靠课程中“空间与几何”典型内容的学习，逐步建立与发展空间观念；（2）依靠教学策略.借助现实情境和学生生活经验来发展空间观念的基础；通过数学实验和问题探究活动，让学生从验证、思考和想象过程中发展空间观念.即从“学”和“教”两个基本途径来培育和发展空间观念.

空间观念能力表征和两个基本的培养途径，虽为教学提供了标杆和基本方法，但没有深入其内涵.空间观念的能力实质是什么？空间观念的能力体现的阶段与层次有哪些？实现这种能力有哪些具体的教学针对？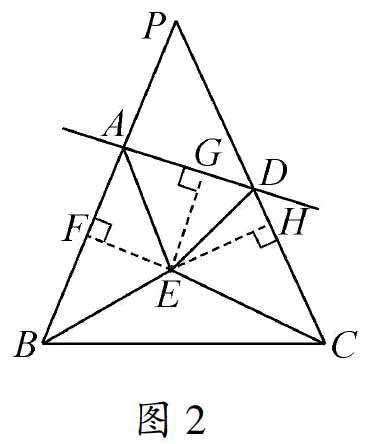

空间观念应具有三层内涵：（1）对图形视觉心理受需要、经验、情绪和意愿的影响很大，需要教师根据学生的认知能力去选择素材、组织活动，排除无数学意义视觉信息，逐步感受形的特征、位置与数量关系.空间观念的建立必须经历“教化后的体验”的感受阶段.如建立图形的方位意识、结构意识、位置与数量关系转化观点等；（2）空间观念是否具有，必须在数学问题中应验，其能动性体现在：对图形数学结构、数量信息再认识，可从图形局部到整体或由表及里（立体几何更明显））地进行合理想象，或对图形做静态向动态有意义的联想和处理，或将图形要素分解、重组、拓展等，以此实现对图形数学事实的发现与认定的感应阶段；（3）获得对空间观念学习与运用的方法、经验、价值与意义的觉悟，使之成为后续学习与发展的数学和世界观的哲学素养，达到空间观念升华的感悟阶段.

以初中教学内容为例，解读空间观念教育的“三感”内涵对教学的启发.

1 空间观念的感受有哪些递进深入的层次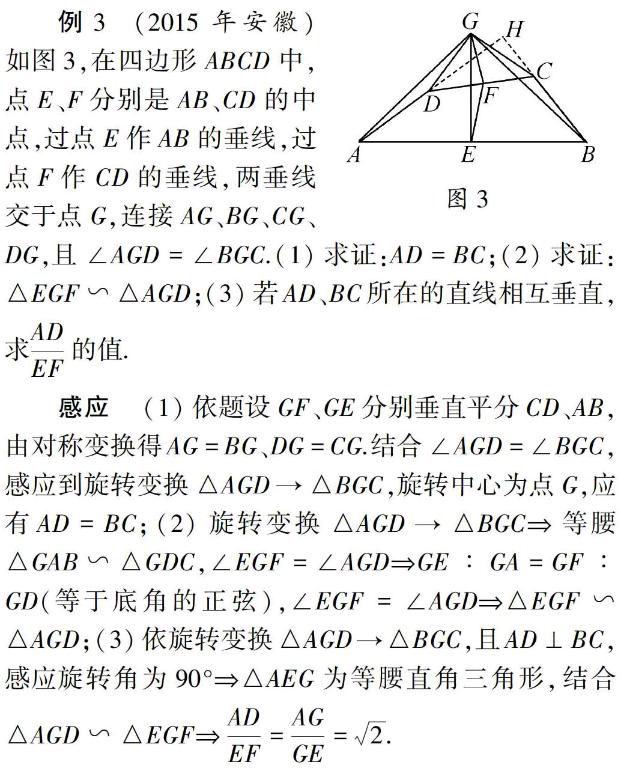

从学的层面看，空间观念的感受是学生对空间与几何的图形元素模型化的结构与意义的体验；从教学的层面看，图形元素被选择、组织、加工后，通过教学载体和学习活动，被学生有思想、有主题地建构，获得有关形的特征、结构、方位、数量关系等方面的认识.这种感受的水平取决于：活动与载体的多样性、有效性.载体可以是看的见的教具、图片和摸得着的学生制作、实验等，还有想起来的生活经验等；活动应源于生活切身体验，对空间与几何的特征、结构、方位意识，成于耳、目、口、手和脑并用之中.

在具体教学中，学生建立空间观念应经历以下递进深入的感受层次：①感受几何对象的概念化过程（或方法）→②感受几何模型的数学元素结构特征或构成方式→③从几何模型结构或生成意识中，感受几何元素位置与数量关系的存在→④感受几何模型的价值与意义→⑤感受几何看法的不断先进与发展.在很多现实的教学中，往往因为匆忙，学生感受没深入这些必经的层次.下面我们列举一些常见的教学不足.

缺失1 学生没有充分感受概念化的过程与方法.如讲到方位角时，教师没有强调谁是“截线”，或没说清同位角的“同位”和内错角的“内错”方位含义各是什么？学生遇到稍微复杂的图形时便很茫然；又如甚至有些学生在中考时还是认不清三角形的高，可能教师没有讲清哪条边上的高与选择引“高”的顶点是什么对应关系.这两个例子，前者说明缺失感受方法，后者是疏忽了感受过程.几何概念的建立是一定的空间观念形成的关键，概念化的过程与方法是对空间的几何要素逻辑化的认识，促成对模型要素关联、有序的看法.

缺失2 学生没有充分感受对几何模型的构成方式的多样性和两种意识.几何模型是获得基本知识的工具，又是解读复杂图形的“基本单位”.对几何模型结构意识是几何思维的基本条件.在现实教学中，很少有教师注意让学生感受几何模型结构理解的多样性.比如在研究三角形内角组合成平角时，教师没注意点化平行线的结构性意义：将分散的内角聚拢成平角，同时将两个内角收拢成另一个内角的邻补角.角与角静态的结构看法：内外角关系、内错角和同位角的方位角关系、邻补角关系；角与角动态的结构看法：有两个内角通过平行线发生了移动，分别形成能组成平角意义的内错角和同位角.这种移动是有主题意义的动态生成.静态的结构意识和动态的生成意识.对几何思维来说，它无时无处不用.学生没有这两种意识，一旦遇到具体问题，深入不到图形元素结构关系中，看不到关联，感觉不到生成.

缺失3 几乎所有的几何模型都是揭示图形特定的结构关系与数量关系（知识）的联系.但是我们在教学时，往往忽视引导学生对空间观念的主题意义的感受.主题意义：①模型化是发现知识的最基本图形要件，空间观念形成的图形看法，最终是把对应关系、位置关系转化为数量关系，空间观念是达到“形”中有“数”的台阶；②空间观念具有一种追求“看法”不断进步的意识，将熟悉的“看法”不断分化、组合，优化为新“看法”.如利用三角形全等去发现角平分线、线段垂直平分线的性质及其逆定理，这就分化出新的空间观念（新看法）：不必再通过三角形全等，直接认同新的位置与数量关系的转化.但是很多教师不注意去启发学生感受空间观念推陈出新的意义.下面的例子就是一个很好的例证：

例1 如图1，已知点C、D是线段AB上方的两点，直线CD与线段AB交于点O，并有AC

=BC和AD=BD.求证：直线CD是线段AB的垂直平分线（2011年黄山市八年级期末统考题）.

试卷分析 在抽样300份试卷中672%的学生能正确证明，其中只有4个考生是用空间观念的新看法来证明：由AC=BC，AD=BD，知C、D是线段AB垂直平分线上的点，根据两点只能确定一条直线，直线CD就是线段AB的垂直平分线.其余的考生都是采用两次以上三角形全等，分步证得“平分”、“垂直”.可见教师平时没有让学生感受“垂直平分线”新看法新观念的意义.

分析空间观念中数学看法的“感受”的内涵与层次，对教学具指导意义：①提高教师对课程设置数学活动意义的理解.比如全等三角形判定方法，各地教材都是用画法所得三角形的唯一性来认同“全等”事实.画法的要义，让学生感受全等三角形空间观念结构与生成意识：通过作图的有序操作，认识全等要素结构关系，以及明白作图要素使得画法生成三角形具唯一性.相反“SSA”的条件操作获得的三角形就不具唯一性；②课本安排的数学活动是以获得空间观念的看法层次深入为目的.比如“轴对称”，以最新的人教版教材为例，数学活动提供的感受层次：①观察图形对称的例子（全等视角）→②操作：剪、贴、画，感受“轴对称图形”具空间拓展的生成性→③从动态生成观点，对“轴对称”的概念化→④观察折线与能重合的对称点或线段的对应、位置关系（结构意识）→⑤获得轴对称数学性质（知识）→⑥会画出轴对称图形（静态结构意识和动态生成观点再体验）.我们的老师是否注意这些感受深入层次？是否又通过有明确的教学设问，去启发学生说看法、想法，了解学生有逐步深入这些层次的感受？

2 空间观念的感应是解决几何问题的思维先导

词典对“感应”一词解释：受事物影响而引起的反应.这里特指空间观念在几何问题中的能动反应.空间观念既有看法上的感受，也有想法上的感应.简单地说，能否从图形的局部去想象出整体；从显性外部去发现隐形的内部；把看似凌乱构图要素做定向选择，做出有序结构化的关联；对图形要素进行分解、重组或延展，按照意愿去改造图形结构；把静态的图形做动态处理（与几何变换有关），从而找到理解、分析和解决问题的线索.对图形的想象力是空间观念感应的核心能力.研究空间观念的感应能力的意义：它是学生发现、分析与解决几何问题的思维先导；研究空间观念的感应类型是教师形成教学思路与策略的依据.

2.1 “伴生”感应推动转化思维

“伴生”是指有些几何条件的运用不是直接的，而是要借助于相伴几何对象来发挥作用，而这些相伴几何对象往往被故意隐去，只有被感应并显化后，解题思路才能形成.

例2 （2013年安徽）在由不平行于BC的直线AD截△PBC所得的四边形ABCD中，∠BAD与∠ADC的平分线交于点E.若EB=EC，请问当点E在四边形ABCD内部时（见图2），四边形ABCD是不是“准等腰梯形”？（即∠ABC=∠DCB是否成立）

感应 想到角平分线上的点到角两边距离相等.过点E分别向直线PB、AD、PC作垂线段EF、EG、EH，应有EF=EG=EH，易得Rt△BEF≌Rt△CEH（HL），∠ABC=∠DCB.四边形ABCD是“准等腰梯形”.

启示 发挥空间观念对条件“伴生”感应，促发对解题转化思维形成，这是解决几何问题很常见的.但是，学生经常想不到这点，一个重要原因：我们老师没有注意培养学生这种“感应”能力，一味从思维方法中捕风捉影.因此，在平时教学中我们应着意提醒学生注意：“角与边”、“比例与平行”、“弧和弦与圆有关的角”的“伴生”现象，建立思考对象的“共同体”，理性添加辅助线.

2.2 “动生”感应促发“变换”思维

“动生”是指图形中含有平移、对称、旋转、位似变换的元素成分，从运动生成的观点看待图形的构成，生发“变换”思维，找到解决问题的方法.

（1）①求∠MPN的度数；②求证：PM+PN=3a；（2）如图52，设点O是AD的中点，连接OM、ON，求证：OM=ON；（3）如图53，设点O是AD的中点，OG平分∠MON，判断四边形OMGN是否为特殊的四边形？并说明理由.

感应 （1）正六边形的外接圆（半径恰好是它的边长），这是背景.以此为“根据地”，显见∠MPN=∠FCD=60°；找到“事发地”：利用PSFM、CDNS和等边△CSP的传“距”：PM+PN=FS+SC+CD，易证②；（2）找到“事发地”：BHMA、PNEH和等边△HBP，用其传“距”、“角”效果，认定旋转变换△AOM→△EON，点O为旋转中心，旋转角120°，OM=ON成立；（3）找到“事发地”：△GOE≌△NOD（ASA），进而认定△MOG、△NOG为等边三角形，四边形OMGN为含60°角的菱形.

启示 “源生”感应是空间观念对数形结合思维的先导.在平时教学中，应引导学生结合题设与求索，对图形区域做解题价值意义的考察.通过合理的联想与甄别，找到或作出能解决问题的“根据地”.

2.4 “仿生”感应促成“类比”思维

发现图形结构与平时几何模型有相似性，可以借鉴模型看法，形成类比思维，发现解题线索.这种空间观念的感应，形象为“仿生”感应.

例6 （2009年安徽）如图6，M为线段AB的中点，AE与BD交于点C，∠DME=∠A=∠B=α，且DM交AC于F，ME交BC于G.

（1）写出图中两对相似三角形；（2）连接FG，如果α=45°，AB=42，AF=3，求FG的长.图6

启示 几何模型的教学不仅为建构知识，同时也为空间观念的“仿生”感应提供素养.平时教学应注意启发学生从问题找到曾是“相识”的感应.此外要强化经典模型感受，如教材中“赵爽图”证明勾股定理、用分类讨论和化归方法证明圆周角定理等用到图形，捡拾中考考法，找到它们的影子，让学生借鉴“仿生”感应，获得类比思维灵犀.下面这个例子就是典型的“仿生”感应：

例7 （2010年上海）如图7，在斜截的圆柱中，已知圆柱的底面直径为40cm，母线最短50cm、最长80cm，则斜截圆柱的侧面积S= cm2.

感应 受梯形面积公式推导启示：将斜截的圆柱成双，其一倒置与另一个拼接成圆柱，显然，S=π×40×50+80÷2=2600πcm2.

研究空间观念的感应类型，看清几何思维方法的渊源.几何思维是依据图形发生的，必须借助空间观念的感应机制来发生.长期以来，我们习惯从数学思想方法的探讨来代替几何思维的研究，没有注意“空间感应”对数学思维和教学策略具有资源性意义.

3 空间观念的建立与发展过程应充满对数学的感悟

空间观念是对图形的数学看法与想法，对人的世界观有着积极影响.空间观念的建立与发展过程，应伴随着对孩子追求真、善、美的感悟性教育.真：空间观念尽管是以抽象形式来反映现实世界中形的特征和位置关系，但揭示的位置、数量关系真实存在，如圆锥的体积计算、垂线段最短等，都能从生活实例中得到应验.空间观念说明世界的可知性；善：其一，空间观念是一种对客观世界的善化.经抽象化、概念化、模型化……的处理，使得数学的真理不断凸现.其二，空间观念为数学勤于建造，力于优化，它是数学思维的先导，没有空间观念，很多数学思想方法无所寄宿.其三，空间观念也是一种价值观念，寻求知识力量去改造世界，美化生活，比如现实生活很多发明创造运用了数学空间模型，采用了合理的位置、结构设计；美：空间观念的发展，不仅创造数学静态的形式美，而且也构造出空间运动、变换和生成的动态美，更重要的是催生数学知识、思想、方法的智慧美.因而空间观念是用数学眼光去探寻世界隐深的精彩与绝妙，应视为人生哲学中的精粹.教师应深挖其内涵，推敲孩子能感触、欣赏的题材，唯美动情地去给予孩子智慧、道德和精神层面上的感悟.下面这个例子就是很好的感悟性教育的题材：

感悟 空间观念的能动性和创造性魅力无限！通过对空间图形的感应与优化，获得更好的证法.

空间观念之所以列为数学十大核心概念之一，是因其对发展人的数学能力和提高数学素养影响力之大.它的内涵和教育功能，还有待于我们从多个层面和角度去探索、挖掘.本文“三感”只是浅水而渔，求简取易，要将其深化于数学教育思想和成效于教学手段、方法，还有待于同仁共勉.