关于变速器各档换算到输入轴的转动惯量当量的计算方法探讨
2016-01-07叶光海,邓方贞
关于变速器各档换算到输入轴的转动惯量当量的计算方法探讨
叶光海1邓方贞2
(1.格特拉克(江西)传动系统有限公司;2.江西机电职业技术学院)
摘要:本文针对目前整车制造企业关注的变速器各档换算到输入轴的转动惯量当量参数问题,从能量的角度分析推导,通过对变速器总成实例介绍,对该参数的计算方法进行了探讨。
关键词:转动惯量当量转动惯量能量速比方法探讨变速器回转状态传动关系
近年来随着汽车工业的发展,特别是我国汽车产业发展政策及汽车产业调整与振兴规划的陆续出台。国内具有一定规模的整车制造企业,纷纷上马自主品牌项目。整车的设计开发模式开始由过去的引进、消化、模仿的模式向自主研发、参数化计算、仿真分析的模式转变。变速器作为整车最重要的传动部件之一,其设计的优化,在适应整车的动力性、燃油经济性及NVH的分析和研究的需要更为重要和迫切。近几年来,在变速器总成匹配开发的过程中,经常会有客户需要我们提供变速器总成的惯量及各档换算到输入轴的转动惯量(以下简称各档转动惯量当量)等参数供整车性能分析。转动惯量作为变速器优化设计的重要参数之一,对整车的轻量化设计,燃油经济性和NVH的分析具要重要意义。对变速器总成的转动惯量,我们都很清楚,可以通过转动惯量定理或平行轴定理来计算获得,也可以通过现在常用的PRO-E等3D软件计算获得,但对于各档转动惯量当量却经常因不知如何换算而回绝了客户。为此,本文就变速器各档转动惯量当量的计算作一探讨。
先说转动惯量的由来,从动能说起大家都知道动能的实际物理意义是:
物体相对某个系统(选定一个参考系)运动的实际能量,用公式表示如下:

把v=ωr代入上式(ω是角速度,r是半径,在这里对任何物体来说是把物体微分化分为无数个质点,质点与运动整体的重心的距离为r,而再把不同质点积分化得到实际等效的r)
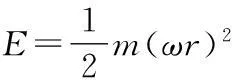
由于某一个对象物体在运动当中的本身属性m和r都是不变的,所以把关于m、r的变量用一个变量J代替,
J=mr2
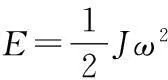
J就是转动惯量,分析其在实际情况中的作用相当于牛顿运动平动分析中的质量的作用,都是一般不轻易变的量。
这样分析一个转动问题就可以用能量的角度来分析了,而不必拘泥于只从纯运动角度分析转动问题。
对于变速器总成来说,一旦设计完成,其结构形状和传动关系就已经固定,我们可以根据实际需要按给定的转轴依据转动惯量的公式直接计算其转动惯量。但对变速器各档转动惯量当量的计算,涉及变速器内部所有传动回转零件,且各个零件又是绕各自的回转轴运动的,并不是所有的零件都是绕输入轴的轴心来回转的,不能通过转动惯量定义的公式直接计算。但我们可以通过分析变速器内部各回转件之间的传动关系,从能量的角度来找出各零件绕各自转轴的转动惯量对输入轴的影响,如速比。一个定型的变速器总成其速比是固定不变的,且各零件的在变速器内的回转运动是按一定的速比有规律地进行的。
下面就以某变速器为例对各档转动惯量当量的计算进行探讨,如图1所示:
根据转动惯量公式,可以算出所有回转件相对于各自安装中心的转动惯量。为方便各档转动惯量当量的计算方法探讨,我们可以按以下方法来对变速器各零件的转动惯量进行叠加和简化:将变速器置于空档状态,①固定输出轴,则所有相对于输入轴轴心的回转运动的零件(含支承轴承内圈及其滚动体)的转动惯量的和为Jr;②固定输入轴,则所有相对于输出轴轴心回转运动的零件(含支承轴承内圈及其滚动体)的转动惯量的和为Jc;③空套于各轴上的档位齿轮(包括其对应的滚针和同步锥)转动惯量分别为一档J1、二档J2、三档J3、四档J4、五档J5、倒档JR、倒档惰轮Jo;④差速器总成的转动惯量为Jd。假定变速器总成各档速比分别为一档I1、二档I2、三档I3、四档I4、五档I5、倒档Ir(Ir1×Ir2)及主减Id

图1 以某变速器为例对各档转动惯量当量的计算
在变速器各档转动惯量计算之前,我们必须清楚变速器总成内部所有回转零件的回转状态或传动关系,这样才能找出各零件自身的转动惯量和各档转动惯量当量之间的关系。现在我们就可以应用动能定理按档位对变速器内部各零件的运动状态依次进行分析,找出变速器各档转动惯量当量的计算方法。假设变速器内部各回转件从发动机获得的总动能为Eei,则:
(1)
其中Jei—表示各档转动惯量当量(i=0,1,2,3,4,5,r,i=0时表示空档状态),
ωei—表示输入轴的角速度(i=0,1,2,3,4,5,r,i=0时表示空档状态)。
1.空档:
当变速器置于空档,汽车是没有输出的,也就是说变速器差速器总成和输出轴是静止的,角速度为零。但所有固定安装于输入轴的零件、输入轴轴承内圈及其滚动体将以ωei角速度回转,因是空档状态,该角速度用ωe0表示。空套安装在输出轴上的一二档齿轮将按各自的档位速比获得的角速度回转,假设各自获得的角速度分别为ω1和ω2,根据速比关系,则一二档齿轮与输入轴的角速度关系为ω1=ωe0/I1,ω2=ωe0/I2,同理可以找出空套于输出轴上的五档齿轮和倒档齿轮及倒档惰轮相对于输入轴的角速度关系分别为ω5=ωe0/I5,ωR=ωe0/Ir,ωo=ωe0/Ir1。空套于输入轴的三四档输入齿轮,因输出轴静止而静止。则空档状态变速器内部各回转件运动的总动能计算如下:
(2)
(3)
按变速器各档传动速比关系:ω1=ωe0/I1,ω2=ωe0/I2,ω5=ωe0/I5,ωR=ωe0/Ir,ωo=ωe0/Ir1
(4)
将(3)和(4)代入式(2)可得:
将上式整理可得:
Je0=Jr+J1(1/I1)2+J2(1/I2)2+J5(1/I5)2+JR(1/Ir)2+Jo(1/Ir1)2
(5)
其中Je0即为该变速器总成内部回转件空档运行时相对于输入轴的转动惯量当量,式(5)即为该变速器总成内部回转件空档运行时转动惯量当量的计算公式。
2.一档:
当变速器置于一档,汽车将以一档速度行驶,变速器输入轴将获得ωe1的角速度,输出轴及固定安装于该轴上的零件及一档齿轮将按一档的角速度回转,根据速比关系,可得其回转角速度为ω1=ωe1/I1,由于此时一档齿轮与输出轴及其附件将通过接合齿轮联结成一个整体,且绕相同的转轴回转,可以进行惯量叠加,惯量为J1+Jc。同时差速器总成受输出轴的驱动工作,根据传动速比关系,获得ωd=ωe1/I1/Id的角速度,所有空套于输出轴及输入轴上的其它档位齿轮将按各自速比获得的角速度空载运行,根据各自传动速比关系,可得:ω2=ωe1/I2,ω3=ωe1*I3/I1,ω4=ωe1*I4/I1,ω5=ωe1/I5,ωR=ωe1/Ir,。则一档状态变速器内部各回转件运动的总动能计算如下:
(6)
(7)
按变速器各档传动速比关系:ω1=ωe1/I1,ω2=ωe1/I2,ω3=ωe1*I3/I1,ω4=ωe1*I4/I1,ω5=ωe1/I5,ωR=ωe1/Ir,ωo=ωe1/Ir1,ωd=ωe1/I1/Id
(8)
将(7)和(8)代入式(6)可得:
将上式整理可得:
Je1=Jr+(J1+Jc)(1/I1)2+J2(1/I2)2+J3(I3/I1)2+J4(I4/I1)2+J5(1/I5)2+JR(1/Ir)2+Jo(1/Ir1)2+Jd(1/I1/Id)2
(9)
其中Je1即为该变速器总成内部回转件一档工作时相对于输入轴的转动惯量当量,式(9)即为该变速器总成内部回转件一档工作时相对于输入轴转动惯量当量的计算式。
3.同理可得,其它档位变速器内部所有回转件换算到输入轴的转动惯量当量,计算式如下:
二档:
Je2=Jr+J1(1/I1)2+(J2+Jc)(1/I2)2+J3(I3/I2)2+J4(I4/I2)2+J5(1/I5)2+JR(1/Ir)2+Jo(1/Ir1)2+Jd(1/I2/Id)2
(10)
三档:
Je3=(Jr+J3)+J1(1/I1)2+J2(1/I2)2+Jc(1/I3)2+J4(I4/I3)2+J5(1/I5)2+JR(1/Ir)2+Jo(1/Ir1)2+Jd(1/I3/Id)2
(11)
四档:
Je4=(Jr+J4)+J1(1/I1)2+J2(1/I2)2+J3(I3/I4)2+Jc(1/I4)2+J5(1/I5)2+JR(1/Ir)2+Jo(1/Ir1)2+Jd(1/I4/Id)2
(12)
五档:
Je5=Jr+J1(1/I1)2+J2(1/I2)2+J3(I3/I5)2+J4(I4/I5)2+(J5+Jc)(1/I5)2+JR(1/Ir)2+Jo(1/Ir1)2+Jd(1/I5/Id)2
(13)
倒档:
Jer=Jr+J1(1/I1)2+J2(1/I2)2+J3(I3/Ir)2+J4(I4/Ir)2+J5(1/I5)2+(JR+Jc)(1/Ir)2+Jo(1/Ir1)2+Jd(1/Ir/Id)2
(14)
根据以上各式计算所得Je0~Je5、Jer即为本变速器总成内部回转件各档换算到输入轴的转动惯量当量值。
从以上关于变速器总成内部回转件各档换算到输入轴的转动惯量当量的计算式推导过程中可以看出,转动惯量当量的计算与变速器转速无关,只取决于变速器内部各零件的自身结构及其传动关系。由于篇幅所限,本文对变速器总成内部各零件的转动惯量及其传动关系进行了一些简化,仅对该参数的计算过程和方法进行了一些分析和探讨。以上所示各计算式,仅适合于与本文示例变速器具有相同或类似结构布局及传动关系的变速器,仅以此抛砖引玉,实际应用于具体的变速器时,可以参考本文示例计算方法,具体分析推导计算。疏漏谬误之处,还望各位专家批评指正。
参考文献
[1]《理论力学》.
[2]《汽车设计丛书变速器》.
