Hilbert空间中一类新广义非线性变分不等式组问题

Hilbert空间中一类新广义非线性变分不等式组问题

罗静1， 隆建军2

(1.四川理工学院理学院， 四川自贡643000；2.攀枝花市大河中学， 四川攀枝花617061)

摘要：变分不等式原理是当今数学技术中一个有力的研究工具，有重要的学术研究价值和意义。在运筹学、计算机科学、系统科学、工程技术、交通和经济与管理等方面有着广泛而重要的应用。利用η-次微分算子的预解算子技巧和辅助原理技术，研究Hilbert空间中的一类广义非线性变分不等式组问题，得出该问题的解。在此基础上，引入一个带有Lipschitz连续、强单调和松弛单调映射的辅助性问题，并且利用预解算子和集值压缩映像的不动点定理证明了解的存在性与唯一性，这一结果推广、改进和发展了相关文献的结果。

关键词：广义非线性变分不等式组；预解式技术；辅助原理技术；迭代算法；收敛性

文章编号：1673-1549(2015)04-0080-06

DOI:10.11863/j.suse.2015.04.17

收稿日期:2015-06-11

作者简介:罗静(1980-)，女，四川自贡人，助教，主要从事数学分析与复变函数理论方面的研究，(E-mail) 379040763@ qq．com

中图分类号：O177.91

文献标志码：A

引言

众所周知，预解算子技巧和辅助原理技术[1]在变分不等式问题中有着十分广泛的应用。近年来，许多学者借助预解算子技巧和辅助原理技术，研究了了Hilbert空间的非线性变分不等式组问题[2-12]。本文在文献[1-5]的基础上，进一步讨论了一类新广义非线性变分不等式组解存在的唯一性，所得结果是文献[2-5]的推广和改进。

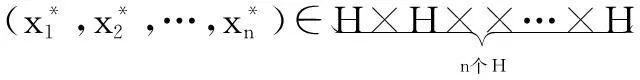
其中，ρi>0为常数。

其中，ρ,γ>0为常数。此问题代宏霞在文献[3]中已经研究。

1基本定义和引理

定义1设非线性映射A(·,·):H×H→H。

(1)称A(·,·)关于第二变元是(a,b)-松弛余强制的，若∃a>0,b>0，使得

[A(·,u1)-A(·,u2),u1-u2]≥-

∀u1,u2∈H

当a=0时，映射A(·,·)就是b-强单调的；因此A(·,·)关于第二变元是(a,b)-松弛余强制映射比A(·,·)是b-强单调映射更具一般性。

(2)称A(·,·)关于第二变元是β-Lipschitz连续的，若∃β>0，使得

(3)称A(·,·)关于第一变元是γ-Lipschitz连续的，若∃γ>0，使得

定义2设η:H×H→H,φ:H→R∪{+∞}，称φ在x处是η-可微的，若∃f∈H使得：φ(y)-φ(x)≥[f,η(y,x)],∀y∈H，并称f为φ在x处的次η-梯度，记∂ηφ(x)为φ在x处所有次η-梯度全体，即

∂ηφ(x)={f∈H:φ(y)-φ(x)≥

[f,η(y,x),∀y∈H]}

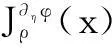
2主要结论及其证明

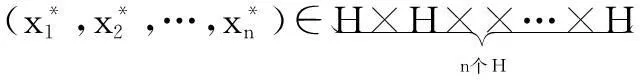
其中，ρi>0为常数。

证明对∀x∈H，广义非线性变分不等式组问题1可化为：

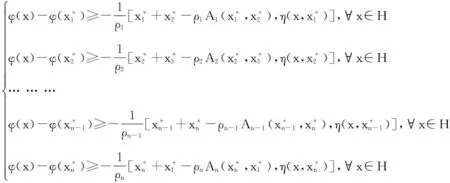
(1)

由η-次微分的定义，不等式组(1)等价于

即

于是广义非线性变分不等式组问题1的解为

证毕。

(2)

其中，ρi>0为常数。

定理2映射Ai(·,·):H×H→H，Ai(·,·)关于第二变元是(ai,bi)-松弛余强制的，且关于第二变元是βi-Lipschitz连续的(i=1,2,…,n)，η:H×H→H满足引理1的条件，假设

(3)

成立，则辅助性问题不等式组(2)有唯一解。

证明定义映射Fw:H→H为：

对任意x,y∈H，有：

(4)

由A1(·,·)关于第二变元是(a1,b1)-松弛余强制的，且关于第二变元是β1-Lipschitz连续的，所以有

(5)

把(5)式代入(4)式，可得

(6)

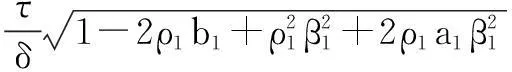
又

(7)

由A2(·,·)关于第二变元是(a2,b2)-松弛余强制的，且关于第二变元是β2-Lipschitz连续的，所以有

(8)

把(8)式代入(7)式，得

(9)

把(9)式代入(6)式，可得

(10)

在(10)式中由Ai(·,·)关于第二变元是(ai,bi)-松弛余强制的，且关于第二变元是βi-Lipschitz连续的(i=3,4,…,n)，所以有

(11)

把(11)式代入(10)式，故有

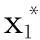
由定理2的辅助性问题(3)式可确定单值映象G;H→H如下：G(w)=x1，其中

定理3假设定理2的所有条件都成立，A(·,·)关于第一变元是γ-Lipschitz连续的，且

成立，那么广义非线性变分不等式组问题1的解存在且唯一。

(12)

其中

即

(13)

又由条件A(·,·)关于第一变元是γ-Lipschitz连续的，故有

(14)

由(12)式、(13)式、(14)式得

即

因为

即

(15)

由(15)式知G(w)=x1是压缩映像，从而存在唯一x1∈H使得G(x1)=x1，即x1是映像G(w)=x1的唯一不动点。由定理2的证明过程中所定义的映象Fw:H→H，令

则

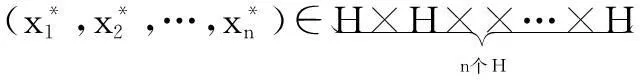
参 考 文 献：

[1]夏锦,苗放.解一类似变分不等式问题的预解式技术和辅助原理技术.四川师范大学学报:自然科学版,2002,25(5):85-486.

[2]陈细法.新的近似算法的广义非线性变分不等式系统.四川师范大学学报:自然科学版,2001,24(6):813-817.

[3]代宏霞.一类广义非线性变分不等式组解的存在唯一性.四川大学学报:自然科学版,2004,41(1):1-4.

[4]任晓.一类广义非线性变分不等式组解的存在性及迭代逼近.四川大学学报:自然科学版,2003,40(3):411-415.

[5]罗元松.Hilbert空间中一般形式的松弛余强制变分不等方程组解的迭代逼近问题.四川大学学报:自然科学版,2007,44(3):467-471.

[6]万波,邓磊.广义集值混合似变分不等式的迭代算法.西南师范大学学报:自然科学版,2008,33(3):1-4.

[7]张玉敏,张国春,刘英.Hilbert空间中关于松弛协强制映射的广义变分不等式组.河北大学学报:自然科学版,2012,32(5):453-457.

[8]彭再云,雷鸣,汪达成,等.希尔伯特空间中的广义余强制变分不等式体系及带误差的三步投影方法.四川师范大学学报：自然科学版,2009,32(2):168-171.

[9]丁协平.一类广义非线性隐拟变分包含.应用数学和力学,1999,20(10):1015-1024.

[10]邱洋青,何思宇.一类广义集值强非线性混合似变分不等式组的迭代算法及辅助原理.南昌工程学院学报,2013(1):18-24.

[11]张彦.一类新的变分包含系统.内江师范学院学报,2012(2):8-11.

[12]李观荣.一类新的广义变分包含系统及其迭代算法.湛江师范学院学报,2014(3):24-29.

[13]Ding X P,Luo C L.Perturbed proximal point algorithma for generalized quasi-variation-like inclusions.J Comput Appl Math,2000,210:153-165.

A New Class of Generalized Nonlinear Variational Inequalities Problem in Hilbert Space

LUOJing1,LONGJianjun2

(1.School of Science, Sichuan University of Science & Engineering, Zigong 643000, China; 2.Dahe Middle School of

Panzhihua, Panzhihua 617061, China)

Abstract:Variational inequality principle is a powerful research tool in the current mathematical technology, and has important academic research value and significance. It is widely and importantly applied in operations research, computer science, system science, engineering technology, transportation, economic and management and other aspects. In this essay, by using the resolvent operator technique and the auxiliary principle technique of η a differential operator, a class of generalized nonlinear variational inequalities problem in Hilbert space is researched, and the solution of the problem is obtained. On this basis, a auxiliary problem with Lipschitz continuous, strongly monotone and relaxed monotone mapping is introduced, and the existence and the uniqueness of the solution are proved by using the resolvent operator and the fixed point theorem of set-valued contractive mappings. This result has extended, improved and developed the results in relevant literatures.

Key words: generalized nonlinear variational inequalities; preconditioning techniques; auxiliary principle technique; iterative algorithm; astringency