测量不确定度的BP神经网络模型
2016-01-07房亚群,吴一凡
测量不确定度的BP神经网络模型
房亚群a, 吴一凡b
(江苏食品药品职业技术学院a.信息工程系;b基础教学部, 江苏淮安223003)
摘要:针对测量不确定评定数学模型无法通过确定的数学关系进行表达的问题,将BP神经网络算法引入测量不确定评定,通过将产生不同确定度的分量的影响因素作为神经网络的输入,合成不确定度和扩展不确定度作为神经网络输出,建立神经网络的不确定评定数学模型。以游标卡尺测量结果不确定度为研究对象,运用BP神经网络不确定评定数学模型,进行不确定评定。仿真结果表明,BP神经网络的不确定评定结果较好、精确度较高,接近于线性预测。
关键词:测量不确定度;BP神经网络;数学模型;合成不确定度;扩展不确定度
文章编号:1673-1549(2015)04-0022-05
DOI:10.11863/j.suse.2015.04.05
收稿日期:2015-06-26
作者简介:房亚群(1981-),女,江苏宿迁人,讲师,硕士,主要从事计算机网络技术及应用方面的研究,(E-mail)495109178@qq.com;吴一凡(1980-),男,江苏淮安人,讲师,硕士,主要从事数学建模方面的研究,(E-mail)wyfdm_1@163.com
中图分类号:TP391.1
文献标志码:A
引言
测量不确定度主要用来表征测量结果不能确定测程度,是衡量测量结果质量的重要指标。GUM中提出的不确定度评定方法容易受到直接测量量相关性的限制,并且计算过程有很多近似,因此计算精度较低,同时操作性较差,现实中操作较为不便[1-3]。神经网络模型具有很强的非线性泛化能力,国内外很多学者都进行了研究。
雷霆等人[4]结合神经网络理论和小波变换技术,提出一种基于小波神经网络的预测模型,运用小波变换技术提取测量序列的特征参数。实验结果证明该方法预测精度较高,但其稳定性较差,有待提高。
Guo Wen等人[5]运用PSO算法对BP神经网络进行全局寻优,并将其应用于粗糙度评定。仿真结果表明,寻优模型的预测精度和收敛速度均好于标准BP神经网络,但PSO算法存在局部最优的问题。
刘渊等人[6]针对小波神经网络存在的缺陷,将混沌理论引入小波神经网络,实证结果表明混沌小波神经网络的预测误差远远小于RBF神经网络的测量不确定度预测结果,但对小波基函数的选择和确定难度较大。
杨光等人[7]利用小波核函数的多分辨率的优点,提出一种基于小波核LS-SVM的测量不确定度评定,实验表明该方法具有一定的优越性,不过参数需要手动确定。
针对神经网络具有优越的非线性泛化能力,本文将BP神经网络算法和测量不确定数学模型进行结合,提出一种基于BP神经网络算法的测量不确定度数学模型,并以(0~2000) mm的游标卡尺测量结果不确定度进行实证分析,通过测量不确定度的BP神经网络的实证分析,建立起游标卡尺的测量不确定度评定模型,实现测量不确定度的自动评定和快速评定,同时排除其他相关因素的限制。
1不确定度数学模型
测量不确定度表征合理地赋予被测量值的分散性,是与测量结果相联系的参数,用来表征和衡量测量结果的质量。在测量不确定度评定中,首先需要建立数学模型,目的是要建立满足测量不确定度评定所要求的数学模型,即建立被测量Y和所有各影响量x间的函数关系,其一般形式为[8]:
Y=f(x1,x2,....,xn)
(1)
2 BP神经网络
BP神经网络由Rumelhart和McCelland1986年研究提出[9-10],是一种误差逆向传播的网络,其结构模型如图1所示,主要由输入层、隐含层和输出层构成。
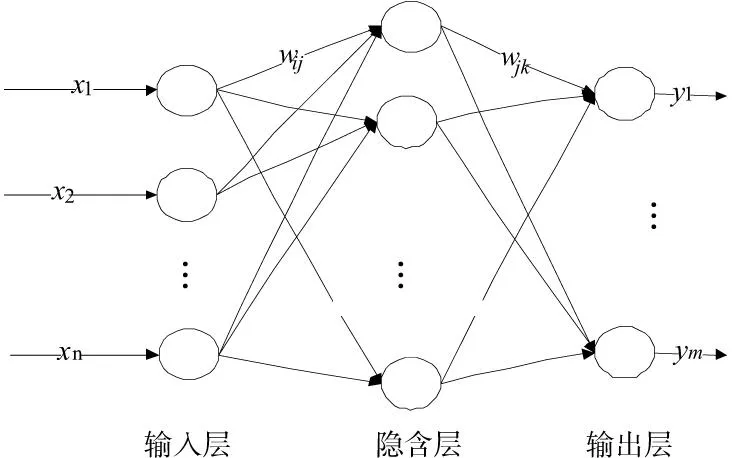
图1 BP网络结构图
图1中,X=(x1,x2,...,xn)表示BP神经网络的输入值;Y=(y1,y2,...,ym)表示神经网络的预测值。
BP神经网络算法的具体流程如下:
Step1:初始化网络。根据神经网络的输入X=(x1,x2,...,xn)和输出Y=(y1,y2,...,ym)确定神经网络的输入层节点数n、隐含层节点数l、输出层节点数m;初始化输入层、隐含层和输出层神经元之间的连接权值wij,wjk;初始化隐含层阈值和输出层阈值,分别为a、b,设定学习速率和神经元激励函数。
Step2:计算隐含层输出。依据输入变量X,输入层、隐含层的连接权值wij和隐含层阈值a,计算隐含层输出H:
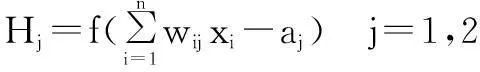
(2)
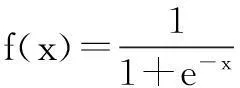
Step3:计算输出层输出。根据隐含层输出H,连接权值wjk和阈值b,计算BP神经网络的预测值O:
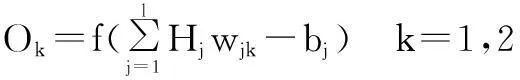
(3)
Step4:计算误差e:
e=Yk-Okk=1,2,...,m
(4)
Step5:更新权值:

(5)
wjk=wjk+ηHjek
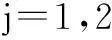
(6)
式(5)和式(6)中,η表示学习速率。
Step6:更新阈值:
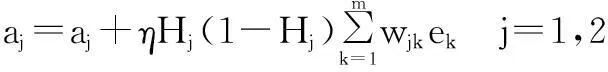
(7)
bk=bk+ekk=1,2,...,m
(8)
Step7:算法停止条件是否满足,若满足,则停止;否则,返回Step2。
3BP神经网络的不确定度数学模型
3.1 建立模型
以(0~2000) mm游标卡尺测量结果的不确定评定为研究对象,建立BP神经网络的测量不确定度评定数学模型(图2)。游标卡尺测量结果的不确定度主要受受检点x1、计量标准本身所具有的不确定度x2、检定环境引起的不确定度x3、被检定器具示值变动性产生的不确定度x4以及测量重复性引起的不确定x5的影响[11]。因此将这个五个变量作为神经网络模型的输入,合成不确定度和扩展不确定作为输出。
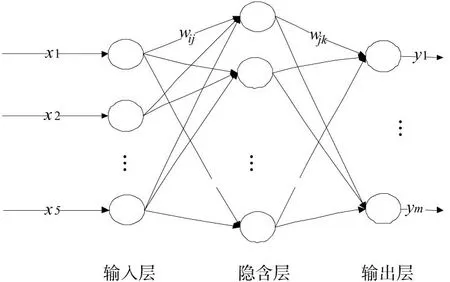
图2 基于BP神经网络的游标卡尺不确定度评定的数学模型
3.2 算法流程图
BP神经网络的不确定度评定流程如图3所示。
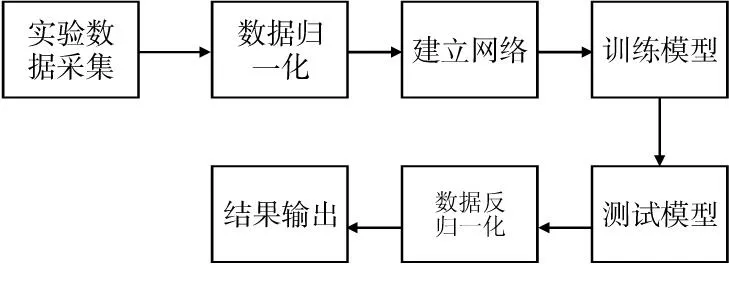
图3 算法流程图
3.3 算法步骤
BP神经网络不确定度评定算法步骤如下:
Step1:构建训练样本以及数据预处理。通过实验进行原始数据采集,获取(0~2000) mm游标卡尺测量结果的不确定数据,数据包括受检点x1、计量标准本身所具有的不确定度x2、检定环境引起的不确定度x3、被检定器具示值变动性产生的不确定度x4以及测量重复性引起的不确定x5以及合成不确定度和扩展不确定,总共采集91组数据。通过归一化进行数据预处理,避免数据数量级不同导致结果偏差过大,同时能够加速网络的收敛速度。
本文归一化采用最大最小法[12]:
(9)
式中,xmin,xmax分别表示数据序列中的最小值和最大值。
Step2:建立BP神经网络模型。将受检点x1、计量标准本身所具有的不确定度x2、检定环境引起的不确定度x3、被检定器具示值变动性产生的不确定度x4以及测量重复性引起的不确定x5作为输入,合成不确定度和扩展不确定作为输出。
Step3:训练网络。采用Levenberg-Marquardt方法[13-14],该方法训练速度快,选取前70组数据作为训练样本。
Step4:测试网络。将后21组数据作为测试样本,验证本文算法的有效性。
Step 5:输出结果并保存网络,方便后期不确定度评定调用。
4仿真分析
4.1评价指标
为了验证本文算法进行测量不确定评定的有效性,采用均方误差用来评价测量不确定评定效果的评价指标[15]。
均方误差:
(10)
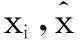
4.2仿真实验
以(0~2000) mm游标卡尺测量结果的不确定评定为研究对象,进行不确定度评定。游标卡尺(10~1050) mm之间分布的70个测量点数据作为训练数据,用于建立神经网络不确定度评定模型;游标卡尺(1100~2000) mm之间分布的21个测量点数据作为测试数据,用于测试所建立不确定度评定网络的好坏。神经网络的参数设置如下:神经网络的参数设置如下:训练目标goal=0.01,训练次数epoch=1000,中间层神经元个数为11,输出神经元为2,输入神经元为5。仿真结果分别如图4~图7所示。
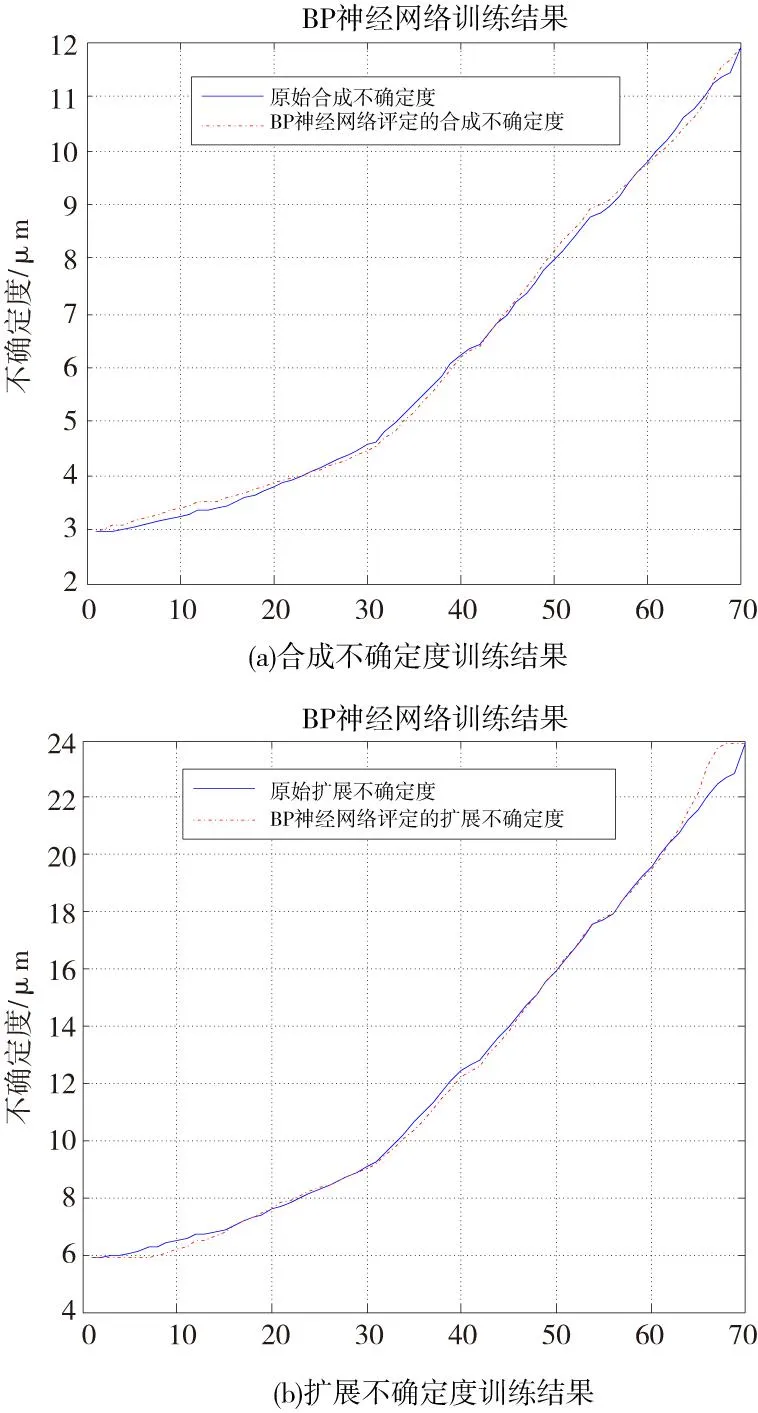
图4 训练结果图

图5 训练误差迭代图
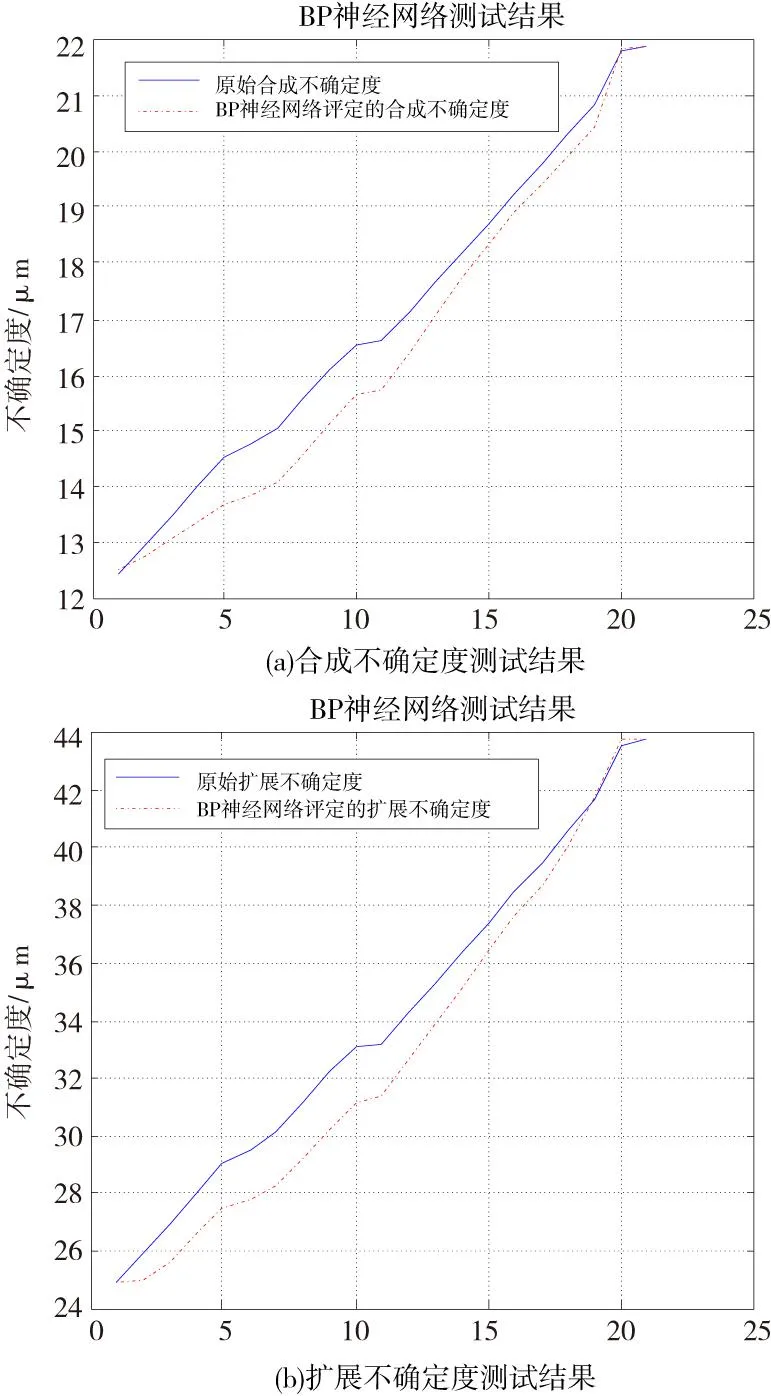
图6 测试结果图
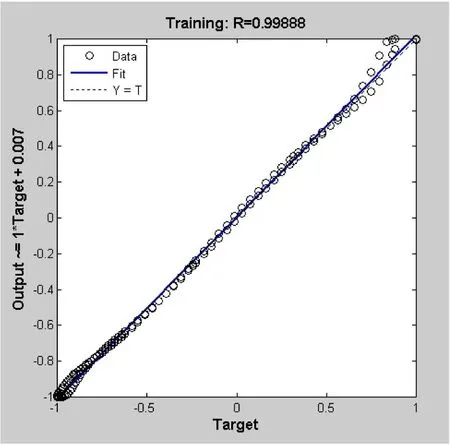
图7 拟合结果图
由图4可知,本文建立数学模型,训练结果较好,合成不确定度和扩展不确定度的原始值和训练结果值拟合效果基本一致,预测的平均相对误差在5%左右,说明网络的训练效果较好。另外由图5可知,网络训练到124次时就达到设置的训练目标值,说明网络的训练速度较快,有助于实际操作。
由图6可知,提出模型的测试结果较好,平均相对误差在7%左右,并且能够满足公式(11)的要求[16]。
(11)
说明测试结果能够满足现实评定的需求。由图7拟合结果图可知,R=0.99888,接近于1,说明预测结果近似于线性预测,效果非常好。
为了验证本文算法的有效性,将本文算法、多元回归和线性回归三者进行对比。运行10次 的预测结果对比见表1;预测时间对比见表2。
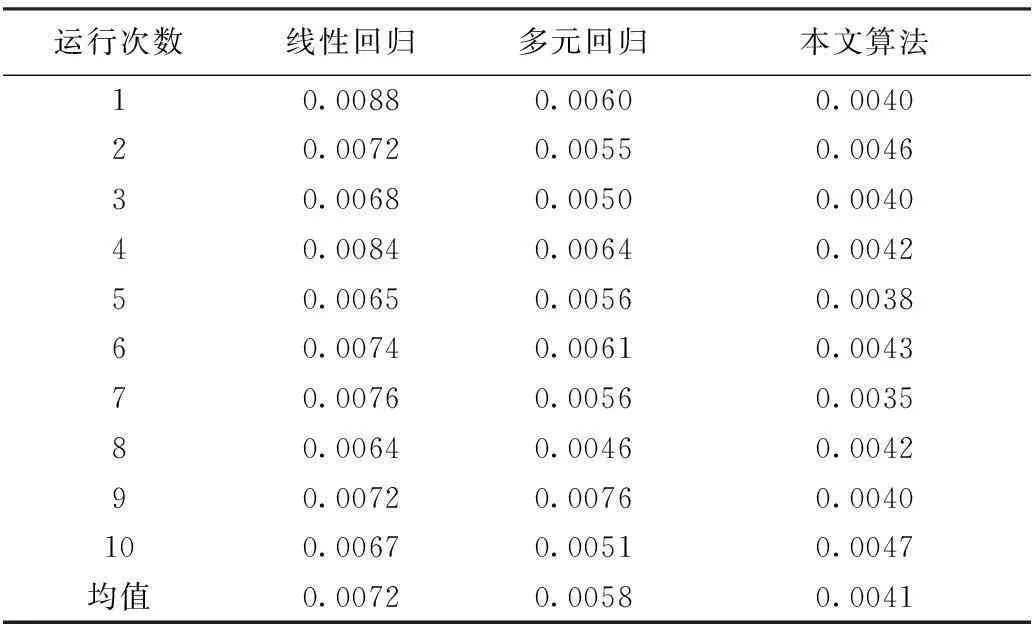
表1 本文算法、多元回归和线性回归预测MSE误差对比
由表1可知,本文算法的预测效果最好,优于多元回归和线性回归模型。
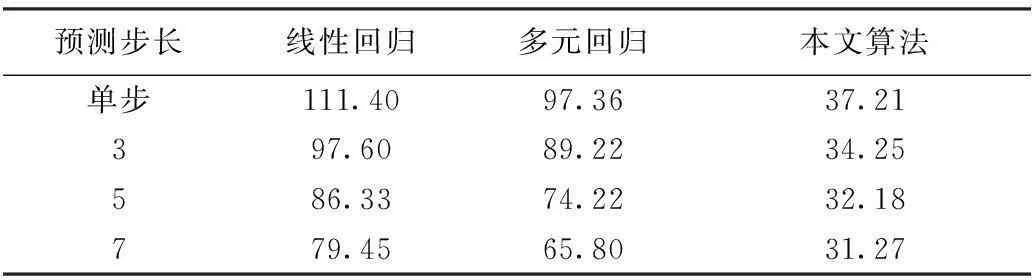
表2 本文算法、多元回归和线性回归预测时间对比(单位:s)
由表2可知,本文算法的预测时间最短,快于线性回归和多元回归模型,而多元回归的预测时间短于线性回归。
5结束语
本文将BP神经网络算法引入测量不确定评定,通过将产生不同确定度的分量的影响因素作为神经网络的输入,合成不确定度和扩展不确定度作为神经网络输出,建立神经网络的不确定评定数学模型。以游标卡尺测量结果不确定度为研究对象,运用BP神经网络不确定评定数学模型,进行不确定评定。仿真结果表明,BP神经网络的不确定评定结果较好,精确度较高,接近于线性预测,同时评定速度较快,有利于在现实中测量不确定度评定的应用和推广。
参 考 文 献:
[1]陈晓怀,薄晓静,王宏涛.基于蒙特卡罗方法的测量不确定度合成.仪器仪表学报,2005,26(S1):759-761.
[2]王伟,宋明顺,陈意华,等.蒙特卡罗方法在复杂模型测量不确定度评定中的应用.仪器仪表学报,2008,29(7):1446-1449.
[3]张海滨,王中宇,刘智敏.测量不确定度评定的验证研究.计量学报,2007,28(3):193-197.
[4]雷霆,余镇危.一种测量不确定评定的小波神经网络模型.计算机应用,2012,26(3):526-528.
[5]Guo Wen,Qiao Yizheng,Hou Haiyan.BP neural network optimized with PSO algorithm and its application in forecasting//Proceedings of the IEEE international Conference on Information Acquisition,Yantai,China,August 20-23,2006:617-621.
[6]刘渊,戴悦,曹建华.基于小波神经网络的时间序列预测.计算机工程,2012,34(16):105-110.
[7]杨光,张国梅,刘星宇.基于小波核LS-SVM 的时间序列预测.微机发展,2011,15(12):125-128.
[8]穆云峰.RBF神经网络学习算法在模式分类中的应用研究.大连:大连理工大学,2006.
[9]Cervellera C,Wen A H,Chen V C P.Neural network and regression spline value functionapproximations for stochastic dynamic programming.Computer & Operations Research,2007,34(1):70-90.
[10]Li Junfeng,Yang Aiping,Dai Wenzhan.Modeling mechanism of Grey Neural Network and its application//Proceedings of 2007 IEEE International Conference on Grey Systems and Intelligent Services,Nanjing,November 18-20,2007:404-408.
[11]叶雪兵,汤洪波.EMC测量系统测量不确定度的评定.计量与测试技术,2007,34(10):15-18.
[12]Mahdavi M,Fesanghary M,Damangir E.An improved harmony search algorithm for solving optimization problems.Appl Math Comput,2007,188(2):1567-1579.
[13]钟国林,李建明,马轲瀛,等.利用吉赫兹横电磁波室实现电能表辐射骚扰测量.中国测试,2011(2):20-25.
[14]Ray T,Saini P.Engineering design optimization using a swarm with an intelligent information sharing among individuals.Eng Optim,2001,33(6):735-748.
[15]李建明,王巍,肖鹏,等.半电波暗室中的EMI辐射骚扰试验测量不确定度分析与评定.中国测试,2012(6):11-16.
[16]Tsai J F.Global optimization of nonlinear fractional programming problems in engineering design.EngOptim,2005,37(4):399-409.
The BP Neural Network Model of Uncertainty Measurement
FANGYaquna,WUYifangb
(a.Department of Information Engineering; b.Department of Basic Courses, Jiangsu Food &
Pharmaceutical Science College, Huai’an 223003, China)
Abstract:In view of the problem that measurement uncertainty evaluation mathematical model could not be expressed by the certain mathematical relationship, the BP neural network algorithm is introduced into the measurement of uncertainty evaluation, the influence factors of component that produce different uncertainty are taken as the inputs of neural network, and the synthetic uncertainty and expanding uncertainty are taken as the neural network outputs, with which the uncertainty evaluation mathematical model of neural network is established. Taking the uncertainty of measurement results with vernier caliper as research object, the mathematical model of uncertainty evaluation of BP neural network is applied to evaluate uncertainty. The simulation results show that the uncertainty evaluation results of BP neural network are good, high precision, close to the linear prediction.
Key words: measurement of uncertainty; BP neural network; mathematical model; synthesis of uncertainty; expanded uncertainty
