L型和矩形低矮房屋体型系数对比研究

L型和矩形低矮房屋体型系数对比研究

姚望1， 姚勇1， 李明2

(1.西南科技大学土木工程与建筑学院， 四川绵阳621010；2.中国空气动力研究与发展中心， 四川绵阳621010)

摘要：通过数值模拟方法与风洞试验结果进行对比，验证了数值模拟方法分析房屋体型系数的可行性。将L型和矩形双坡房屋的屋面体型系数进行对比，将矩形屋面和规范中的体型系数取值进行对比。结果表明：L型房屋的屋面体型系数在绝大多数工况下相对较小，说明L型房屋更有利于抗风，并指出了在规范中当体型系数取值为负时偏小。最后给出了根据实验值计算L型房屋体型系数建议值。

关键词：L型房屋；数值模拟；体型系数

文章编号：1673-1549(2015)04-0057-05

DOI:10.11863/j.suse.2015.04.12

收稿日期:2015-06-02

作者简介:姚望(1990-)，男，四川绵阳人，硕士生，主要从事结构抗震、抗风方面的研究，(E-mail)365982671@ qq．com

中图分类号：TU312+.1

文献标志码：A

引言

根据国内外大量自然灾害统计表明，风灾是一种发生频率高，破坏力强的自然灾害，给人民的生命财产带来了巨大的损失[1]。然而，历次风灾中低矮建筑损失占了房屋破坏总损失的一半以上[2]。因此，对低矮房屋的风载特性进行深入研究很有意义。

国外已经有大量学者对低矮房屋进行了研究[3]。但是，在国内关于低层房屋抗风问题的研究仍未成为结构风工程研究领域的一个重要课题，相关方面的投入和学术关注均很低[4]。

目前，在结构风工程领域采用的研究方法主要有现场实测、风洞实验和数值模拟[5]。风洞试验和数值模拟在风荷载特性分析上都有较好的可行性[6]。但是，风洞试验存在着经费大，周期长，并且很难进行系统分析风荷载等问题。相较于风洞试验，数值模拟方法具有周期短，经费少，准确性高等特点[7]。在近30年的时间里，数值模拟方法已经成了一种分析风荷载的有力工具。

国内外已经较系统地研究了来流风向角、屋面坡度、挑檐长度、檐口高度和房屋长宽比对屋面风压系数的影响[8-11]。这些研究都是在矩形房屋的基础上研究的。实际上，房屋的体型对屋面的体型系数也有影响。随着人们生活水平的提升，房屋的形式不再局限于矩形平面。近年来，L型平面的房屋广为流行[12]。然而，我国《建筑结构荷载规范》[13]只对它们墙体的体型系数作了规定，对屋面体型系数的取值无法查阅。对于低矮建筑，体型的变化对低矮建筑体型系数的影响还没有明确的定论。但可以肯定的是，房屋体型的变化对体型系数具有一定影响。

本文的研究对象是矩形和L型双坡屋面的低矮房屋。在验证数值模拟可行性的基础上，初步探讨低矮建筑体型的变化对房屋体型系数的影响，并对L型房屋相对矩形房屋的抗风能力进行初步评价。

1数值风洞模拟方法

1.1　RNG k-ε模型

近地风实际上可以看成一种不可压缩的湍流流动。在FLUENT软件中，提供了多种用于计算的湍流模型。其中RNG k-ε湍流模型，具有良好的模拟精度，所以，此次试验采用该模型进行模拟。Suh S H等也都先后采用该模型对实例建筑的风场和风压进行过数值模拟，结果表明该模型的模拟效果良好。其湍流微分方程：

(1)

(2)

式中：Gk、Gb、YM和标准K-ε模型相同。αk、αε分别为湍动能和耗散率ε方程的有效湍流普朗特数的倒数。湍流粘性系数ut公式为：

(3)

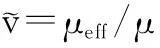
1.2　计算域及网格的划分

本次试验选取的基准模型是矩形平面房屋和L形平面双坡房屋。它们坡角的坡度取为15°、25°、30°、35°、45°和60°。一共有12个模型。模型平面及风向角定义如图1所示。矩形平面的房屋长宽高为15×7.5×9.8 m。L形平面的尺寸如图1所示，高度和矩形平面相同。矩形平面计算流域取为180×90×60 m。L形平面计算流域取为240×160×60 m。建筑物置于流域沿流向前1/3处，流域设置满足阻塞率<3%的要求。

图1　计算模型及风向角定义

为了实现更好的效果，并更好的利用计算资源，此次计算采用混合网格离散方法。计算区域可以分为内外两部分，在靠近模型的区域采用四面体结构化网格，网格布置较密。然后在远离模型的区域，采用具有规则拓扑结构的六面体结构化网格。矩形平面的网格总数为80万个，L形平面的网格总个数为100万个。

1.3　计算参数设置

(1)入口来流条件：对于入口进流处速度的选取，采用《建筑结构荷载规范》给出的指数率风速分布计算公式：

(4)

其中，Z0、U0分别是参考点的高度和风速，参考高度取为10 m，模拟B类地貌的风场，因此α的取值为0.15，风速剖面可以通过UDF应用编程然后于fluent作接口实现。

(2)出口条件：由于出流面接近完全平面，因此，采用完全发展边界条件。流场的任意边界物理量沿出口方向的法方向梯度为0。

(3)流域顶部及两侧：采用自由滑动壁面。

(4)结构表面和地面：采用无滑移的壁面条件。

1.4　计算收敛准则

采用分离式求解，3D单精度计算。用精度较高的二阶迎风格式对流项进行离散。迭代的收敛标准为所有控制方程的相对迭代残余量均小于l×10-4，且同时监测到的各表面压力系数基本不发生变化时，认为所得流场进入了稳态。

1.5　验证算例

本文选取长安大学风洞试验数据，作为数值计算的验证。屋面定义和建筑模型如图2所示。风洞试验中，矩形平面房屋的尺寸为15×7.8×9.9 m，屋面坡角为α=30°。采用数值模拟方法对风洞试验进行对比验证时，矩形的计算流域选取为180×100×80 m。建筑物置于流域沿流向前1/3处，流域设置满足阻塞率<3%的要求。分别在0°、45°和90°风向角下进行对比，体型系数的对比结果如图3所示。

图2　矩形屋面定义

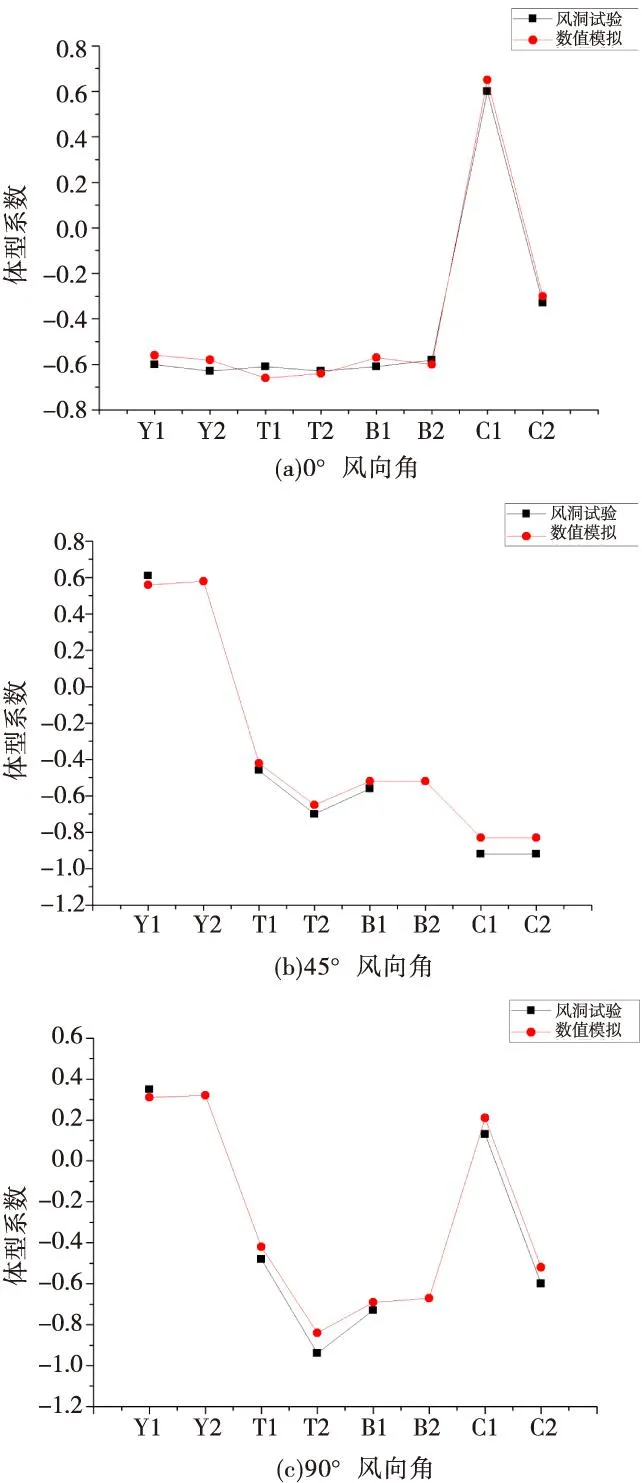
图3　L型和矩形屋面体型系数值

通过数值模拟与风洞试验的对比，可知数值模拟对房屋体型系数的模拟与试验吻合度较好，虽然存在一定的误差，但是误差在工程设计可接受范围之内。因此，采用数值模拟的方法对房屋的风载体型系数进行分析是切实可行的。

2体型系数的对比与分析

2.1　测点风压系数

在计算中为了方便，各计算模型的风压系数CP，可根据《建筑结构荷载规范》取10 m高度处作为参考高度，来流动压作为无量纲化的参考风压。定义为：

(5)

式中，P为测点平均压力，P0参考点处静压，ρ为空气密度，取1.225 kg/m3。U0为参考点处风速，取12.8 m/s。

2.2　面体型系数

点的风压系数测定之后，就可以对建筑体型每个面上测点的风压系数进行加权平均，就可得到面体型系数。

(6)

其中：CPi为第i测点风压系数，Ai为该点所属表面面积，A为表面总面积，Zi为第i测点高度，当Zi<10时，取Zi=10。

2.3　不同坡角下体型系数对比

选取15°、25°、30°、35°、45°和60°坡角矩形和L形低矮房屋，分别在0°～180°风向角下进行体型系数对比。不同工况下的体型系数值如图4所示。

图4　坡度变化下的体型系数

比对方式：L型房屋上部区域在相同风向角下和矩形屋面对比，L1和J2对比，L3和J1对比。下部区域对比时有些差异，在0°和90°风向角下对比时，L2和L4分别和相同风向角下J2和J1对比。45°风向角时，L2和L4分别和135°风向角下的J1和J2对比。在135°风向角下，L2和L4分别和45°风向角下的J2和J1对比。180°风向角下，L2和L4分别和90°风向角下矩形屋面J2和J1对比。

在这样的对比方式下，一共对比了120组数据。在0°风向角下进行对比时，可知只有在15°、25°、30°和60°坡角下，共四组对比中L1和L2的体型系数绝对值比相应的矩形屋面大。最大相差0.26，最小相差0.06。其他情况，L型屋面的体型系数绝对值比相对应的矩形屋面小，屋面的整体风压更小。在45°风向角时，25°坡角下，L1和L3比相应的矩形屋面大，分别大了0.23和0.04。在35°坡角下，L2比相应的矩形更大，60°坡角时，L3比相应的矩形屋面大，分别大了0.07和0.02。其它20组对比中，L型的屋面体型系数都更小。在90°风向角时，15°坡角下L1和L3的体型系数比对应的矩形屋面更大。分别大了0.04和0.18。30°坡角下，L1和L3的比相应矩形更大。分别大了0.02和0.01。45°坡角下，L1和L2的比相应矩形的系数更大，分别大了0.08和0.38。60°坡角下，L2和L3的比相应矩形更大。其它情况下，L型房屋的体型系数更小。当风向角变为135°时，只在45°坡角下的L4和60°坡角下L3区域的体型系数比相应的矩形更大，分别大了0.09和0.05。在180°风向角下，只在60°坡角下的L3和L4比相应的矩形体型系数更大，均大了0.02。

在120组数据的对比中，只有24组数据，L型房屋的体型系数绝对值更大，其他96组数据的体型系数绝对值都更小，差值大多在0.1以上。体型系数小的屋面整体抗风性能更好。因此，L型房屋在绝大多数情况下对抗风更有利。

3规范取值的对比

《建筑结构荷载规范》中对矩形房屋的体型系数作了规定。该系数取值和本文中135°风向角下矩形屋面的情形相对应(图5)。

和规范的对比中可知，在迎风面，

当规范取值为负数时，取值比数值模拟的结果更小。当规范中取值为正数时，取值比数值模拟结果更大。在背风屋面中，规范统一取为-0.5，而数值模拟的结果比该值的绝对值更大。因此可知，当屋面承受负压时，体系系数取值的绝对值偏小，偏于不安全。当屋面承受正压时，体型系数取值偏于安全。

图5　规范中矩形屋面体型系数取值

4L型房屋体型系数建议值

鉴于《建筑结构荷载规范》中并没有给出L型屋面的体型系数值。因此，根据本文的实验值给出L型双坡屋面的体型系数建议值，可以给L型屋面的抗风设计提供参考，见表1。

表1　L型房屋屋面体型系数建议值

注：本表只适用于上部结构和下部结构长度较为接近的L型房屋。

5结论

本文对两尺寸一样的矩形房屋组成的L型房屋在平均风作用下的风压系数值进行了探讨，并分别在15°、25°、30°、35°、45°和60°坡角下和单栋的矩形平面房屋进行了对比。得到如下结论：

(1)通过数值模拟得到的屋面体型系数和风洞试验得到的结果误差较小，验证了用数值模拟方法分析房屋体型系数的方法是切实可行的。

(2)L型低矮房屋屋面的体型系数在绝大多数工况下，体型系数值相比矩形屋面都更小，表明L型屋面的整体风压更小，对于抗风更有利。

(3)体型的变化、屋面坡度、挑檐长度、檐口高度和房屋长宽对房屋的体型系数有影响。

(4)当矩形屋面承受负压时，《建筑结构荷载规范》中取值偏小，使得在进行抗风设计时，屋面偏于不安全。

参 考 文 献：

[1]孙高勇,姚勇,李明.低层双坡屋面风压标准k-ε模型模拟研究.西南科技大学学报,2013,28(1):25-30.

[2]孙炳楠,傅国宏.9417号台风对温州民房破坏的调查//七届全国结构风效应学术会议论文集.重庆:重庆大学出版社,1995.

[3]顾明,赵雅丽,黄强,等.低层房屋屋面平均风压的风洞试验和数值模拟.空气动力学学报,2010,28(1):82-87.

[4]杨伟.基于RANS的结构风荷载和响应的数值模拟研究.上海:同济大学,2004.

[5]陈水福,吕少琳.低层双坡房屋屋面风荷载的数值研究-坡角和高宽比影响的分析.浙江大学学报,2006,40(10):17-38.

[6]顾明,黄强,黄鹏,等.低层双坡房屋屋面平均风压影响因素的数值模拟研究.建筑结构学报,2009,30(5):2-5.

[7]周绪红,聂少锋,周天华,等.低层双坡屋面建筑三维定常风场的数值模拟.工程力学,2010,27(3):19-29.

[8]王辉,陈水福,唐锦春.低矮坡屋面群体建筑表面风压的数值模拟.工程力学,2003,20(6):135-140.

[9]Holmes J D.Wind pressures on tropical housing.Journal of Wind Engineering an Industrail aerodynamics,1994,53:105.

[10]Xu Y L,ReardonG F.Variations of wind pressure on hip roofs with roof pitch.Journal of Wind Engineering an Industrail aerodynamics,1998,73:267-284.

[11]赵雅丽,全涌,黄鹏,等.典型双坡屋面风压分布特性风洞试验研究.同济大学学报:自然科学版,2010,38(11):1586-1592.

[12]陶玲,黄鹏,顾明,等.L形平面低矮房屋屋面的风荷载特性.同济大学学报:自然科学版,2011,39(11):1586-1591.

[13]建筑结构荷载规范:GB 50009—2012.

A Comparative Study on the Shape Coefficients of

L-shape and Rectangular Low-rise Buildings

YAOWang1,YAOYong1,LIMing2

(1.School of Civil Engineering and Architecture, Southwest University of Science and Technology,

Mianyang 621010, China; 2.China Aerodynamics Research and Development Center, Mianyang 621000, China)

Abstract:At first, the feasibility of using numerical simulation method to analyze building shape coefficient is verified by comparing the results of the wind tunnel test with it. Then the roof shape coefficients of L-shape and rectangular gable buildings are compared, and the shape coefficient of the rectangular roof is compared with that in standard. The results show that the roof shape coefficients of L-shape buildings are relatively smaller under most of the working conditions, which means that the L-shape buildings are more advantageous for wind resistant. The results also point out that the shape coefficients in the norm are small when the number is negative. Finally, the shape coefficient values which are used to calculate L-shape buildings based on test values are suggested.

Key words: L-shape buildings; numerical simulation; shape coefficient