基于RBF神经网络的Duffing混沌系统控制
2016-01-07周群利
基于RBF神经网络的Duffing混沌系统控制
周群利
(芜湖职业技术学院电气工程学院, 安徽芜湖241006)
摘要:采用基于RBF神经网络的控制方法对Duffing混沌系统进行控制,运用RBF神经网络对受控的Duffing系统动力学方程中的非线性项进行自适应逼近,在保证受控系统在原点处的平衡态是一致渐进稳定的前提下,设计了相应的控制律及自适应控制律,使系统的状态变量在很短时间内稳定地收敛于目标值,仿真结果证明了该方法的有效性。
关键词:混沌控制;Duffing系统;RBF神经网络;自适应;非线性
文章编号:1673-1549(2015)04-0041-04
DOI:10.11863/j.suse.2015.04.09
收稿日期:2015-05-18
作者简介:周群利(1978-),女,陕西西安人,讲师,硕士,主要从事非线性控制方向的研究,(E-mail)zhouqunli2011@163.com
中图分类号:TP13
文献标志码:A
引言
Duffing方程是用来描述外力作用下非线性阻尼振荡系统,其方程特点之一是在其右端加上了强迫项,系统的本征频率与外加周期强迫项频率的相互作用,使得在该方程中蕴涵着极其丰富的内容:倍周期分叉、奇怪吸引子、吸引子与复杂的流形结构共存等[1]。这类系统引起了许多学者的研究兴趣[2-3]。当Duffing方程中的参数取一定值时,系统呈混沌状态。混沌是非线性动力学系统中一个非常有意义的现象,混沌现象表现出复杂性、类噪声性、不可预测性等行为[4]。针对Duffing方程混沌系统,众多学者已提出许多不同的控制方法[5-11],其中,文献[5]研究了基于Lyapunov方法的稳定控制问题;文献[6]研究了基于状态观测器的混沌控制方法;文献[7-8]研究了外加激励的混沌控制方法;文献[9]研究了状态反馈混沌控制方法;文献[10-11]研究了自适应混沌控制方法[12]。由于RBF神经网络能逼近任意非线性函数,因而可大大加快学习速度并避免局部极小问题,适合于实时控制的要求。本文采用基于RBF神经网络的方法对Duffing混沌系统进行控制,使系统状态稳定地收敛于目标值,被控系统的混沌轨道按照既定目标轨道运动,从而将混沌系统无序的状态变量稳定控制在不稳定的周期轨道上,因此混沌系统的同步控制与混沌系统的镇定问题是非常有意义的。
1Duffing系统的动力学方程及状态响应
Duffing系统的动力学方程为:

(1)
当系统参数p=0.2、 p1=1、p2=1、q=36、w=0.661时,系统处于混沌状态。式(1)又可写为:
(2)
取系统状态初值为[0.5 0.5]T进行仿真,可得到Duffing系统相轨迹图(图1),可以看出系统的状态变量变化毫无规律,其相轨迹在混沌吸引子内绕着子吸引子盘绕折叠,在当前参数取值下,系统的状态完全进入混沌态。

图1 Duffing系统相图
2基于RBF神经网络的Duffing混沌系统控制方法
在式(2)中第二个方程的右端施加控制u,受控的Duffing系统即变为:
(3)


(4)
式中,x为网络的输入;bj为一个正的标量,表示高斯基函数的宽度;j为网络隐含层的第j个节点。网络的输出为:
f(x)=WTh(x)+ε
(5)
式中,W为神经网络的理想权值;h为高斯基函数的输出,h=[hj]T;ε为神经网络的逼近误差。
基于文献[13]中的RBF神经网络逼近原理,采用RBF神经网络逼近f(x),网络输入取x=[x1x2]T,根据式(5),RBF神经网络的输出可表示为:
(6)

构造Lyapunov函数为:
(7)

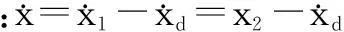
定义误差函数为:
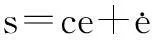
(8)
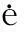
对式(7)求导可得:
(9)
由式(8)可推导出:
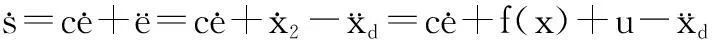
(10)
设计控制律为:
(11)
将式(11)代入式(10)得:
(12)
而
(13)
将式(13)代入式(12)得:
(14)
设计自适应控制律为:

(15)
将式(15)代入式(14)可得:
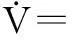
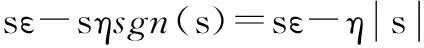
(16)

3仿真结果及分析
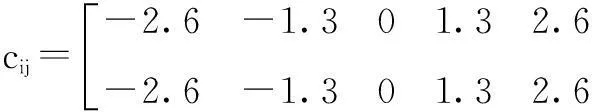

图2 x 1的状态响应曲线

图3 x 2的状态响应曲线
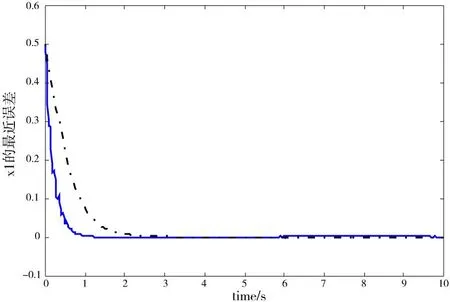
图4 x 1的逼近误差曲线
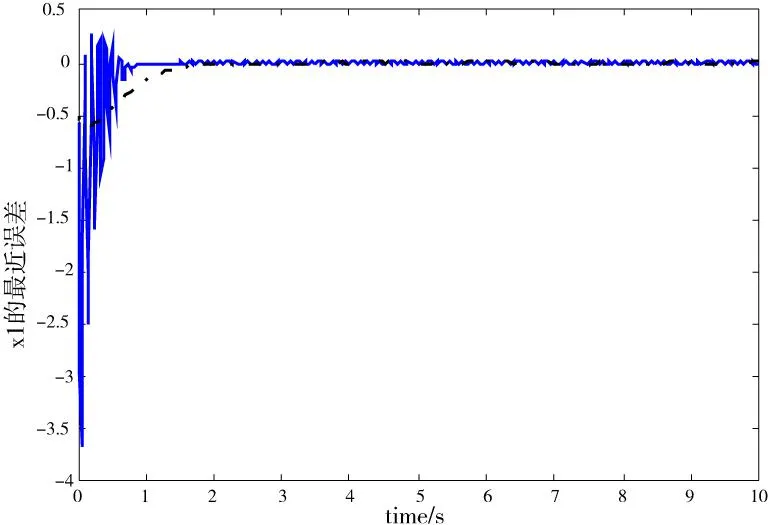
图5 x 2的逼近误差曲线
图2~图5中,蓝色粗实线为采用基于RBF神经网络的跟踪控制方法得出的系统x1、x2的状态响应曲线及其跟踪误差曲线,粗虚线为采用文献[9]的反馈线性化跟踪控制方法得到的系统x1、x2的状态响应曲线及其跟踪误差曲线。从以上仿真图形可以看出:采用基于RBF神经网络的跟踪控制方法,Duffing系统的状态变量大约在1 s内可稳定跟踪状态目标值,受控的Duffing混沌系统的状态变量x1即可达到稳定,收敛于状态目标xd(t)=sin(t),同时,状态变量x2也达到稳定,收敛于状态目标cos(t);而采用反馈线性化的跟踪控制方法,稳定跟踪状态目标值大约需要2 s。因此,相比较,基于RBF神经网络的跟踪控制方法比反馈线性化的跟踪控制方法跟踪效率更高、速度更快。
4结束语
采用基于RBF神经网络的控制方法对Duffing系统的混沌行为进行控制,使系统状态在很短时间内稳定地收敛于设定的状态目标值,消除了混沌,仿真结果证明了该方法的有效性。此研究为其他非线性不稳定系统的控制提供了一种行之有效的解决思路,可应用于保密通讯、信号处理、激光物理、化学反应、生物医学等领域。
参 考 文 献:
[1]方锦清,姚伟光.逆算符方法求解非线性动力学方程及其一些应用实例.物理学报,1998,42(9):1379.
[2]Jian Z P.Advanced feedback control of the chaotic duffing equation.IEEE Trans. Circuits Syst.I.,2002,49(2):244-249.
[3]Xu H B,Lu B C,Chen G J.Chaotic control of the duffing equation in the presence of uncertainty.Systems Engineering and Electronics,2000,22(2):15-16.
[4]刘乐柱,张季谦,许贵霞,等.一种基于混沌系统部分序列参数辨识的混沌保密通信方法.物理学报,2014,63(1):010501-1~010501-6.
[5]徐红兵,吕炳朝.基于Duffing方程不确定性模型的混沌控制.系统工程与电子技术,2000,22(2):15-17.
[6]刘健,宋珊珊,刘美菊,等.一种基于状态观测器的Duffing系统的混沌控制.沈阳建筑大学学报:自然科学版,2009,25(2):395-398.
[7]沈建和,陈树辉.混沌Mathieu-Duffing振子的开闭环控制.应用数学和力学,2009,30(1):21-29.
[8]褚衍东,李险峰,张建刚.Van der Pol-Duffing耦合系统的分岔与混沌控制.江南大学学报:自然科学版,2007,6(1):119-123.
[9]周群利,张绍德.基于反馈线性化的Duffing混沌系统控制.安徽工业大学学报,2007,24(1):58-61.
[10]王中生,李伟峰,廖晓昕.不确定Duffing混沌系统控制的自适应跟踪控制.华中科技大学学报:自然科学版,2005,33(2):64-66.
[11]周培培,曹鸿钧.Helmholtz-Duffing振子同宿分岔的自适应反馈控制.科学技术与工程,2008,8(7):1769-1773.
[12]赵黎明.Duffing 混沌系统的全局快速Terminal滑模变结构控制.沈阳理工大学学报,2011,30(3):34-36.
[13]刘金琨,沈晓蓉,赵龙.系统辨识理论及MATLAB仿真.北京:电子工业出版社,2013.
Duffing Chaotic System Control Based on RBF Neural Network
ZHOUQunli
(School of Electrical Engineering, Wuhu Institute of Technology, Wuhu 241006, China)
Abstract:The control method based on RBF neural network is adopted to control Duffing chaotic system. The nonlinear terms of controlled Duffing system’s dynamic equation are adaptly approached by RBF neural network. In order to ensure the premise of the equilibrium at the origin of the controlled system is asymptotically stable, the corresponding control law and the adaptive control law are designed, for which the state variables of the system can stably converge to the target value in a short period of time.The simulations results show that the method is effective.
Key words: chaotic control; Duffing system; RBF neural network; adaptive; nonlinearity
