宽浅河道瞬时源源项反问题及反演精度主要影响因子分析

宽浅河道瞬时源源项反问题及反演精度主要影响因子分析

吴一亚1,2,金文龙3,吴云波1,2,韩龙喜3

(1.江苏省环境科学研究院,江苏 南京210037; 2.江苏省环境工程重点实验室,江苏 南京210037;

3.河海大学环境学院,江苏 南京210098)

摘要：根据宽浅河道的水动力特性和可溶性污染物在河道内的迁移转化特征,建立了宽浅河道内突发性瞬时源污染物排放位置及污染物排放量的数学反问题;采用微分进化算法,给出了反问题的数学求解方法;构造典型案例,利用瞬时源污染物浓度平面分布的理论解,对反问题求解方法进行了验证;并采用情景分析方法,进一步分析了事故应急监测点位、监测频次对污染源反演精度的影响。结果表明,反演精度依赖于监测点位的数量、监测频次等影响因子,基于一定观测数据、观测精度的污染源的数学反演,可以为瞬时源强、发生位置的确定提供技术佐证。

关键词：宽浅河道;瞬时源;源强;反问题;反演精度;影响因子

基金项目：国家水体污染控制与治理科技重大专项(2012X07506-007)

作者简介:吴一亚(1990—),女,硕士,主要从事环境水力学研究。E-mail:wuyiya0915@126.com

中图分类号：X522

文献标志码：A

文章编号：1004-6933(2015)05-0058-04

Abstract：According to the hydrodynamic characteristics of wide and shallow rivers and the transfer characteristics of soluble pollutants in rivers,a mathematical inverse problem about location and intensity of instantaneous pollution source in wide and shallow rivers is established. The solving method of this problem is given using differential evolution algorithm. A typical case is set out and the solving method is verified using the theoretical solution of concentration plane distribution of instantaneous pollution source. Based on the scene analysis method,further analysis is made to analyses the influence of monitoring sites and monitoring frequency on inversion accuracy of the pollution source. The results indicate that: the inversion accuracy depends on several influencing factors including the number of monitoring sites and monitoring frequency. The mathematical inverse problem of pollution source based on certain monitoring data and monitoring accuracy can provide technical support on determining the intensity and location of instantaneous pollution source.

收稿日期：(2014-11-05编辑：徐娟)

Inverse problem of instantaneous source in wide and shallow rivers and

analysis on main influencing factors of inversion accuracy

WU Yiya1,2,JIN Wenlong3,WU Yunbo1,2,HAN Longxi3

(1.JiangsuProvincialAcademyofEnvironmentalSciences,Nanjing210037,China;

2.JiangsuProvincialKeyLaboratoryofEnvironmentalEngineering,

Nanjing210037,China;

3.CollegeofEnvironment,HohaiUniversity,Nanjing210098,China)

Key words： wide and shallow rivers; instantaneous source; source intensity; inverse problem; inversion accuracy; influencing factor

近年来,地表水突发污染事故频频发生,对于某些事故(如船舶运输化学品的泄漏),由于存在不确定性,很可能在事故初期无法确定污染源的发生位置以及污染物排放源强等基本参数,从而给事故的预警预报和处置处理工作带来困难。因此,科学、准确地识别污染源信息是水污染事故预警及应急处置的关键基础工作。

水污染事故发生后,可通过事故发生后的水质应急监测数据来反推污染源信息,数学语言表达为利用污染物时空分布的部分信息，反推出污染物迁移转化相应的源项,在环境水力学学科中可归纳为源项识别的反问题[1]。该方面的研究正越来越受到研究者的广泛关注,如:Akcelika等[2]采用变分有限元方法求解了对流扩散输运的源项反演问题;Wang等[3]提出了多孔介质流动中的源项识别马尔科夫随机场模型;Cheng等[4]使用反向位置概率密度函数法和CCHE2D模型程序对河流污染源进行了识别;韩龙喜等[5]构造并求解了河网地区带约束条件的污染源控制反问题;陈媛华等[6]利用相关系数优化法对一维河道的单点瞬时排放源进行了反演;朱嵩等[7]采用贝叶斯方法进行了污染源识别和模型参数的反演研究;王泽文等[8]研究了流域中单个点污染源识别问题的唯一性、稳定性和反演算法。近年来,遗传算法等现代优化算法在求解源项反问题中得到应用,闵涛等[9]将对流-扩散方程源项识别反问题转化为优化问题,并用遗传算法求解;韩龙喜等[10]以污水处理费用最小为目标函数,采用遗传算法求解了带约束条件的污染物排放量控制反问题;Jae等[11]利用遗传算法建立区域污水处理最优化的水质管理模型。笔者所采用的微分进化算法作为一种较新的优化算法,具有算法简单、容易实现、较强的全局搜索能力等优点,因此也逐渐开始被用于地表水污染源的识别。

总体而言,前人的研究主要集中于污染源排放位置已知情况下的污染源源强的控制和识别问题;缺少关于事故应急水质监测方案(包括监测点位布设数量、监测频次等)主要影响因子对源项反演精度的影响研究与探讨。因此,笔者基于突发瞬时源在宽浅河道中的迁移转化特征,依据事故下游的水质监测数据,构造了瞬时源源项识别反问题;在反问题的求解方法上,运用微分进化算法,该方法作为一种较新的优化算法,具有收敛速度快、可调参数少、计算精度高、稳定性好的独特优势,使用该方法对污染物排放位置和排放数量进行了反演,并且探讨了监测方案(包括监测点布设数量、监测频率)中各类监测因子对反演结果精度的影响。研究结果将为更科学精确地识别污染源信息,并为事故应急监测预案的制定、优化提供重要的技术参考;同时,所应用的反问题求解方法以及对于影响反演精度因子的考虑在地表水污染源的识别上具有重要意义。

1宽浅河道瞬时源迁移扩散二维水质模型

假定事故发生水域为河流宽深比足够大的所谓宽浅河道,不妨假定河道内污染物的背景浓度值为0。假定在时间t=0时刻,在平面二维坐标(xm,ym)处瞬时进入水体的污染物质量为M,则由此产生的污染物的浓度增量C随时间和空间的变化规律可用二维对流-扩散方程来描述:

(1)

式中:ux、uy分别为水流在纵向、横向上的流速分量;t为时间；Dx、Dy分别为污染物的纵向、横向弥散系数;K为污染物的降解系数;Mδ(x-xm,y-ym,t)为源项,其中M为瞬时源排放的污染物数量,xm,ym为点源在二维空间上的坐标,δ(·)为狄拉克函数;C0为瞬时源初始浓度。

式(1)构成了宽浅河道瞬时源二维水质模拟分析的数学模型,即正问题,其理论解为

(2)

2源项反问题的构造及数学求解方法

2.1宽浅河道瞬时源数学反问题构造

在突发性水污染事故中,往往很难及时监测到污染源的源强大小和污染源的位置,即此时式(1)中的M和(xm,ym)未知,因此无法采用水质模型对事故引发的水质影响进行及时预警预报。为确定源项,可在事故下游设置若干监测点,从而获得一组污染物浓度的监测资料,其数学描述为

(3)

式中:Cobs(xi,yi,tj)为第i个测点、第j个时序的污染物浓度监测值;k为测点总数;ni为第i个测点监测频次总数。

通过上述污染物浓度的监测值确定源强大小M和污染源位置(xm,ym),可构成宽浅河道瞬时源源项识别反问题。假定S为由M和(xm,ym)构成的待定向量函数,将定解问题(1)对应于S的解记为C(S,x,y,t),则上述反问题可转换为如下优化问题:

(4)

即以各监测点不同监测时间的监测值与计算值之差的平方和最小为目标函数,计算满足条件的最优解S。

2.2源项反问题的求解方法——微分进化算法

微分进化算法应用了“优胜劣汰,适者生存”的自然进化法则,属于演化算法。微分进化算法可以求解间断系数的识别问题,包括偏微分方程反问题中的源项识别反问题、参数识别反问题和初始条件反问题等。微分进化算法在求解偏微分方程反问题时,基本上不依赖搜索空间的知识或其他辅助信息,而仅用特定的适应性函数来评价个体,并在此基础上驱动演化,且对适应性函数本身并没有特别严格要求,因此它的应用非常广泛,尤其适合处理传统优化方法难以解决的高度复杂的非线性问题,具有智能型、多解性、全局优化性、随机性和稳健性的特点。

与传统演化算法相比,实现了种群的进化,保留了结果的最优性。

3污染源反问题算例及求解方法验证

如图1所示,不妨假定宽浅河道研究区域长3000m,宽150m,平均水深h=1.0m,平均流速u=0.65m/s,分散系数Dx=4.0m2/s,Dy=0.5m2/s。污染事故发生在xm=500m,ym=50m处,在t=0时刻瞬时事故排放污染物量M=2000kg,降解系数K=0.0001d-1。

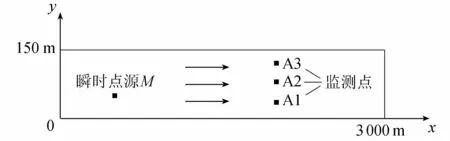
图1　宽浅河道污染源反演算例示意图

监测方案设定:不妨假定,在事故发生后第1200～3700s时间段进行监测,监测位置为A1(2000,40)、A2(2000,80)、A3(2000,120),监测频次为每隔500s监测1次,每个监测点均监测6次。

(5)

参数取值:微分进化算法种群规模20,交叉概率0.1;交叉因子0.5,最大进化代数为500。用微分进化算法程序进行计算,反演结果见表1。

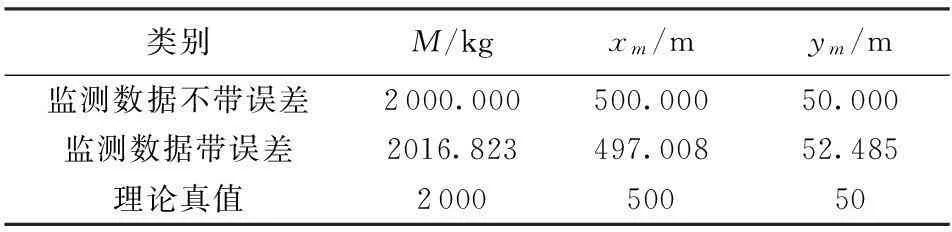
表1　源强大小及位置反演结果

反演结果表明,当监测数据直接由正问题的解析解得到,不附加误差时,反演结果与真实值相同;当监测数据带有一定的误差时,反演结果存在一定误差,但误差很小,反演结果能正确反应污染源排放的真实情况。由此可知,求解方法能准确反演污染源的大小和位置。

4监测方案对反演精度的影响

水污染事故发生后的污染源强的准确反演,依赖于对监测点位水质的准确定量描述。因此,监测方案(监测点位数量、监测频次)对污染源的反演精度有重要影响。

4.1监测点位数量对反演精度的影响

为独立分析监测点位布设数量对源强反演精度的影响,采用情景分析方法,假定在同样的监测起止时间(1200—3700s时间段)和监测频次(每隔500s监测1次)的前提下,分别设置1个监测点位(A2(2000,80))、2个监测点位(A1(2000,40)和A2(2000,80))及3个监测点位(A1(2000,40)、A2(2000,80)、A3(2000,120))等3种工况,采用数值试验,定量分析监测点位布设数量对瞬时源的源强反演精度的影响。为描述问题简便计,不妨不附加干扰。源强反演精度用相对误差EM定量描述,源强位置反演精度用绝对误差Ex,Ey描述。

不同监测点位布设数量对应的源强反演精度如表2所示。

表2　不同监测点位数源强反演结果

由表2的反演结果可知,当监测点位只有1个时,反演误差很大,不能正确反映污染源的真实情况;当监测点位为2个或2个以上时,反演结果与污染源的真实情况十分接近。

4.2监测频次对反演精度的影响

在同样监测点位(不妨设为A1和A2)和监测起止时间(1200～3600s)的前提下,分别假定监测频次为2、3、4、5、6次5种工况,不附加干扰,定量分析监测频次多少对反演精度的影响。结果见表3。

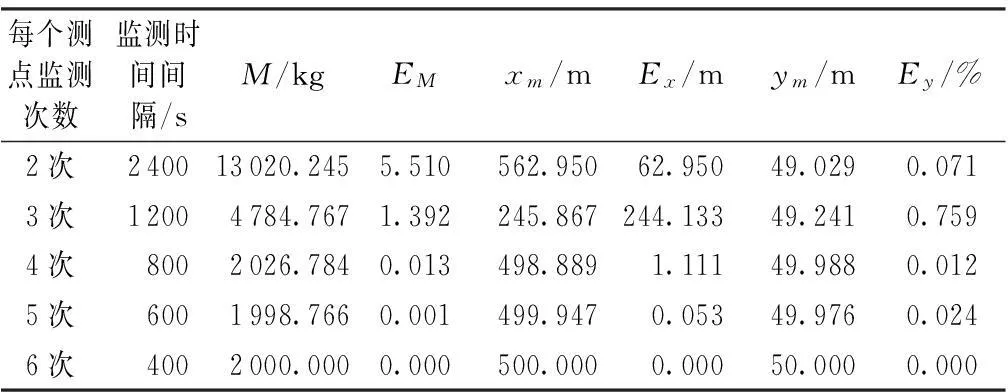
表3　每个测点不同监测频次的反演结果

反演结果表明,在设置2个监测点位情况下,监测频次少于4时,源强反演结果存在较大误差,无法正确反演污染源排放污染物的真实情况;当监测频次等于4时,反演结果基本能反映真实情况;当频次大于4时,反演结果较为准确。总体而言,在监测点位固定的情况下,监测频次越高,反演的精度越高,因此,在制定监测方案时,应尽量提高监测频次,以保证反演结果的可靠性。

5结语

对于宽浅河道,基于平面二维水质模型,构造了污染源源强及位置的反问题,给出了反问题的数学求解方法,并对求解方法进行了验证。数值试验研究表明,反演精度依赖于监测点位的数量、监测频次等影响因子,基于一定观测数据、观测精度的污染源的数学反演,可以为瞬时源强发生位置的确定提供技术佐证。本文研究方法依据的正问题采用的是水质模型的理论解析解,但同样适用于基于水质模型数值解法构建的反问题。

参考文献：

[1] 刘晓东,姚琪,薛红琴,等. 环境水力学反问题研究进展[J]. 水科学进展,2009,20(6): 885-890. (LIU Xiaodong,YAO Qi,XUE Hongqin,et al. Advance in inverse problems of environmental hydraulics[J]. Advances in Water Science,2009,20(6): 885-890. (in Chinese))

[2] AKCELIKA V,BIROS G,GHATTAS O,et al. Avariational finite element method for source inversion forconvective-diffusive transport [J]. Finite Elements in Analysis and Design,2003,39: 683-705.

[3] WANG J,ZABARAS N. Using bayesian statistics in the estimation of heat source inradiation [J]. International Journal of Heat and Mass Transfer,2005,48: 15-29.

[4] CHENG W P,JIA Y. Identification of contaminant point source insurface waters based on backward location probability density function method[J]. Advances in Water Resources,2010,33(4): 397-410.

[5] 韩龙喜,朱党生. 河网地区水环境规划中的污染源控制方法[J]. 水利学报,2001(10): 28-31. (HAN Longxi,ZHU Dangsheng. The pollutant source control method for network water environment management [J]. Journal of Hydraulic Engineering,2001(10): 28-31. (in Chinese))

[6] 陈媛华,王鹏,姜继平,等. 基于相关系数优化法的河流突发污染源项识别[J]. 中国环境科学,2011,31(11): 1802-1807. (CHEN Yuanhua,WANG Peng,JIANG Jiping,et al. Contaminant point source identification of rivers chemical spills based on correlation coefficients optimization method [J]. China Environmental Science,2011,31(11): 1802-1807. (in Chinese))

[7] 朱嵩,刘国华,王立忠,等. 水动力-水质耦合模型污染源识别的贝叶斯方法[J]. 四川大学学报:工程科学版,2009,41(5): 30-35. (ZHU Song,LIU Guohua,WANG Lizhong,et al. A bayesian approach for the identification of pollution source in water quality model coupled with hydrodynamics [J]. Journal of Sichuan University:Engineering Science Edition,2009,41(5): 30-35. (in Chinese))

[8] 王泽文,邱淑芳. 一类流域点污染源识别的稳定性与数值模拟[J]. 水动力学研究与进展: A辑,2008,23(4): 364-371. (WANG Zewen,QIU Shufang. Stability and numerical simulation of pollution point source identification in a watershed[J]. Chinese Journal of Hydrodynamics,2008,23(4): 364-371. (in Chinese))

[9] 闵涛,周孝德,张世梅，等. 对流-扩散方程源项识别反问题的遗传算法[J]. 水动力学研究与进展: A辑,2004,19(4): 520-524. (MIN Tao,ZHOU Xiaode,ZHANG Shimei,et al. Genetic algorithm to an inverse problem of source termidentification for convection-diffusion equation [J]. Chinese Journal of Hydrodynamics,2004,19(4): 520-524. (in Chinese))

[10] 韩龙喜. 河道一维污染源控制反问题[J]. 水科学进展,2001,12(1): 39-44. (HAN Longxi. Inverse problem on amount of pollutant into natural channel [J]. Advances in Water Science,2001,12(1): 39-44. (in Chinese))

[11] CHO J H,SUNG K S,HA S R. A river water quality management model for optimizing regional wastewater treatment using a genetic algorithm [J]. Journal of Environmental Management,2004,73(3): 229-242.