多维VG过程下的一篮子期权定价

杜子平　邱虹

【摘 要】 一篮子期权属于多标的资产的一个投资组合期权。由于不能明确地知道股票间的相依结构，因此一篮子期权的定价结果需要采用逼近或者通过Monte Carlo数值仿真的方法获得。经典的Black & Scholes模型不能描述对数收益率“尖峰厚尾”等特征，而Variance Gamma（VG）过程却能很好地拟合观测到的对数收益率。文章提出了一种在多维VG过程下的一篮子期权的定价方法。一篮子中的股票价格是由带有共同Gamma从属因子的变时几何布朗运动构造的。选取德国DAX指数进行检验，结果表明多维VG过程可以很好地匹配德国DAX指数的市场观测值。

【关键词】 一篮子期权； Lvy过程； 多维VG过程

中图分类号：F831.59 文献标识码：A 文章编号：1004-5937（2015）23-0064-05

一、引言

如今，多资产衍生品的交易量日益增多，一篮子期权就是金融市场上一类新型的多资产期权，是多标的资产的一种投资组合，经常用来对一篮子资产进行套期保值，其收益是由一篮子标的资产的加权算术平均价格来决定，并且比单一资产进行投资组合所花的费用更少。由于投资者追求风险最小化，故对这种投资组合分散化的期权进行定价研究有一定的现实意义。

1973年Black & Scholes提出了经典的期权定价理论，同年Merton利用偏微分方程求解期权定价公式的解。其假定标的资产服从几何布朗运动，此种方法给出了封闭形式下的vanilla期权定价公式。但现实中的金融市场可能由于突发战争、国家发生政治经济等政策变化、人为投机事件以及投资者心理变化导致金融市场发生跳跃现象，使得金融时间序列呈现“尖峰厚尾”非高斯、非对称的特征。故Black & Scholes模型（下文简称B-S模型）出现“波动率微笑”定价偏差。因此本文引进一个更加灵活的Lvy过程来描述金融市场的信息。

国内方面，奚炜（2003）在期权定价解析解的基础上，用恒生指数期权进行实证分析，结果显示VG期权定价模型比传统的B-S模型更能准确地描述金融市场，是一种理想的改进模型。刘国光等（2006）通过Lvy过程中的NIG模型和VG模型对中国市场中的沪深股指收益分布特征与国外主要的股市股指收益分布特征进行拟合对比分析。刘志东等（2010）利用标准普尔500指数、上证综指、恒生指数，在不同Lvy过程下进行参数估计，并给出符合现实环境的解释。

基于当前的研究现状，本文利用多维VG过程对一篮子期权进行定价，并通过德国DAX指数对模型进行检验。

二、模型

（一）B-S模型

1973年，金融学领域的一个重大突破是由学者Fischer Black和Myron Scholes利用连续时间数学发展出看涨期权定价模型。他们发表了《期权定价与公司债务》（The pricing of option and corporate liabilities）。该模型对交易员定价和对冲期权的方式产生了极大影响，也对过去20年金融工程的发展和成功起了关键性作用。1997年，Myron Scholes和Robert Merton被授予诺贝尔经济学奖。令人惋惜的是，Fischer Black在1995年去世，否则他无疑也是该奖项的获得者之一。

B-S期权定价公式，即无收益资产欧式看涨期权的定价公式为：

C=P×Nr（YA）-Se-Rft×Nr（YB）

其中：YA=[In（P/S）+Rft+σ2 t/2]σt1/2

YB=[In（P/S）+Rft-σ2 t/2]σt1/2

式中，Rf为无风险利率（投资者可通过购买无违约风险的政府债券获得），与期权价格正相关；P是标的资产的现行市场价值（价格），与期权价格正相关；σ表示标的资产价值的波动程度，由收益率的方差（σ2）或标准差（σ）来测度，与期权价格正相关；S是期权合约的行权价格，与期权价格负相关；t为期权到期日距离现在的时间长度，与期权价格正相关。In代表以e为底的对数运算，而Nr代表正态累积概率密度函数，测度正态分布随机变量等于或小于Y的概率。

B-S模型是在有效市场的假说下，假定一个连续变化的资产价格在未来任何时刻都服从对数正态分布。也就是，其假定资产的价格服从布朗运动，是一个连续随机过程。由于对数正态分布本身有完美的数学特征：均值和方差可唯一确定分布函数，同时还具有可加性，因此标准布朗运动和对数正态分布在资产定价中广泛使用。然而，更多的实证分析可得，资产收益率的经验分布是“尖峰厚尾”，这是由于金融市场中某些特殊事件引发不正常的突发事件。Lvy过程以法国数学家Paul Lvy命名，因其假设条件相对比较宽松，能同时描述连续和跳跃过程，故笔者引入其来描述标的资产的“尖峰厚尾”和“非对称”特征，更加符合现实结论。

（二）VG过程

Merton（1976）建立了跳—扩散模型，Kou（2002）提出了一种可以替代Merton模型的双指数跳跃模型（Kou Model），这两个模型都是有限活动Lvy过程。Kou模型相比Merton模型的优势在于，具有指数随机变量的无记忆特性。以下为无限活动纯跳跃Lvy过程：Madan & Seneta（1990）研究了澳大利亚股票市场的数据，提出了VG过程；Barndoff-Nielsen（1997）建立了正态逆高斯模型（Normal Inverse Gaussian Processes，NIG过程）为主要代表的广义双曲线过程（Generlized Hyperbolic）；Schoutens & Teugels（1998）在文献中介绍了Meixner过程。Carr（2002）等提出的CGMY模型是以Carr、Geman、Madan和Yor命名的，许多学者也将此分布族称为KoBoL族。Rachev（2005）、Rosiski（2007）研究发现带跳的金融市场，资产收益率尾部往往是在正态分布和稳态分布之间，因此修正了稳态分布，建立了高效的调和稳态Lvy过程（tempered stable processes）。其中VG过程和CGMY模型都是调和稳态Lvy过程的特例。

Madan & Seneta（1990）提出了VG过程，其作为股票收益率的一种来构建对数定价模型。这种模型的选择是在研究澳大利亚股票市场的数据时得出的。它是以Gamma过程为从属过程进行累加驱动的，通过变时后作用于标准布朗运动而得到新的布朗运动，且Gamma过程是无限可分的。

VG过程是金融领域中使用最广泛的一种Lvy过程，也称为贝塞尔函数分布（Bessel function distribution），是典型的无限纯跳过程。利用偏度（skewness）和峰度（kurtosis）来描述厌恶风险的程度和厚尾分布等特征。VG过程的特征三元组为（σ，？自，？兹），分别表示布朗运动的波动率、Gamma过程在任意时刻变化的方差率以及布朗运动的线性漂移率。

VG过程的定义如下：

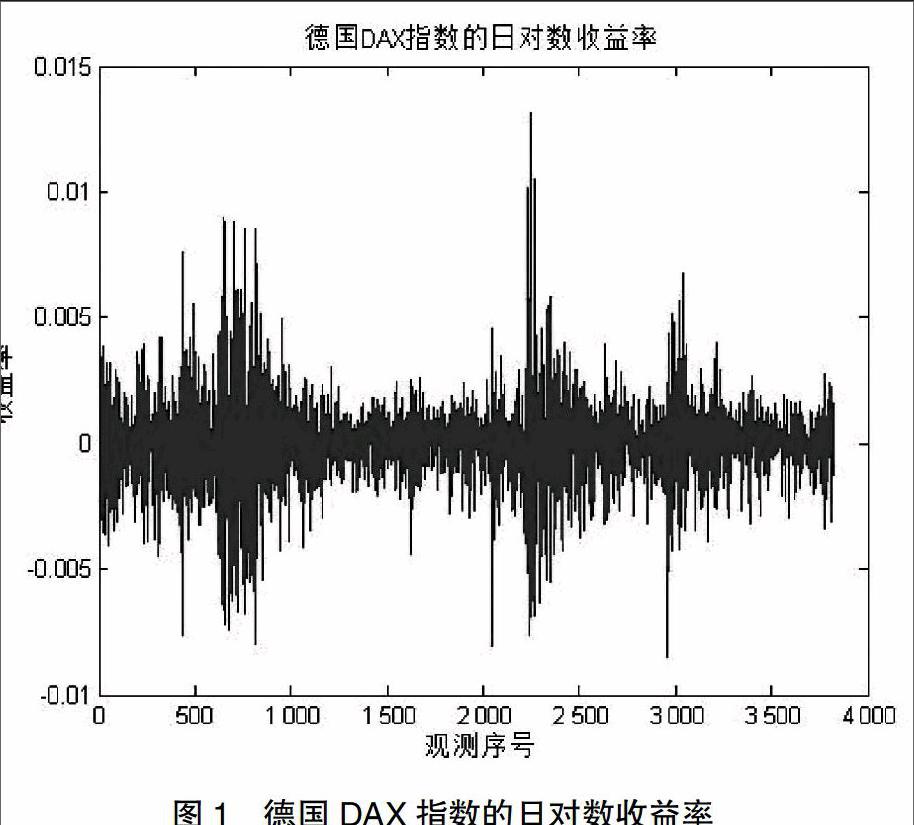
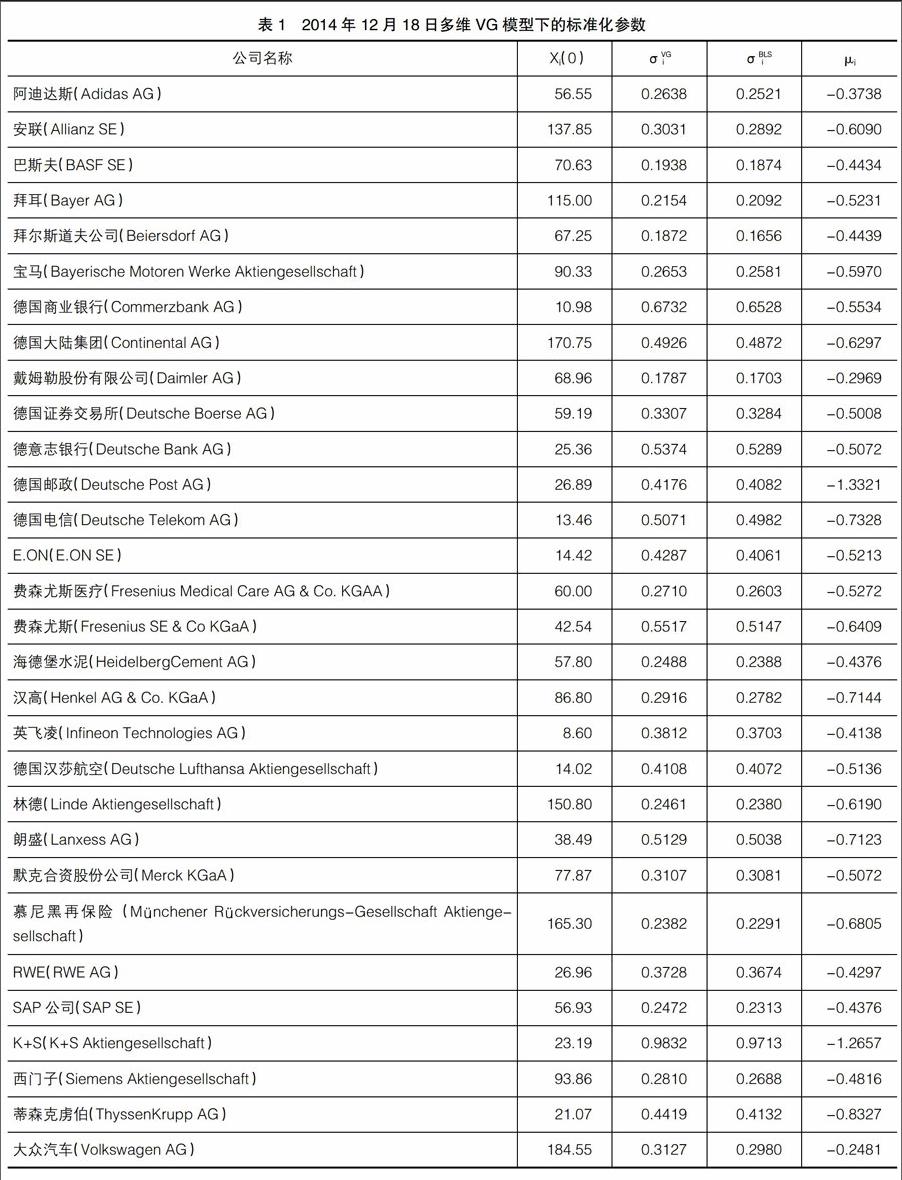
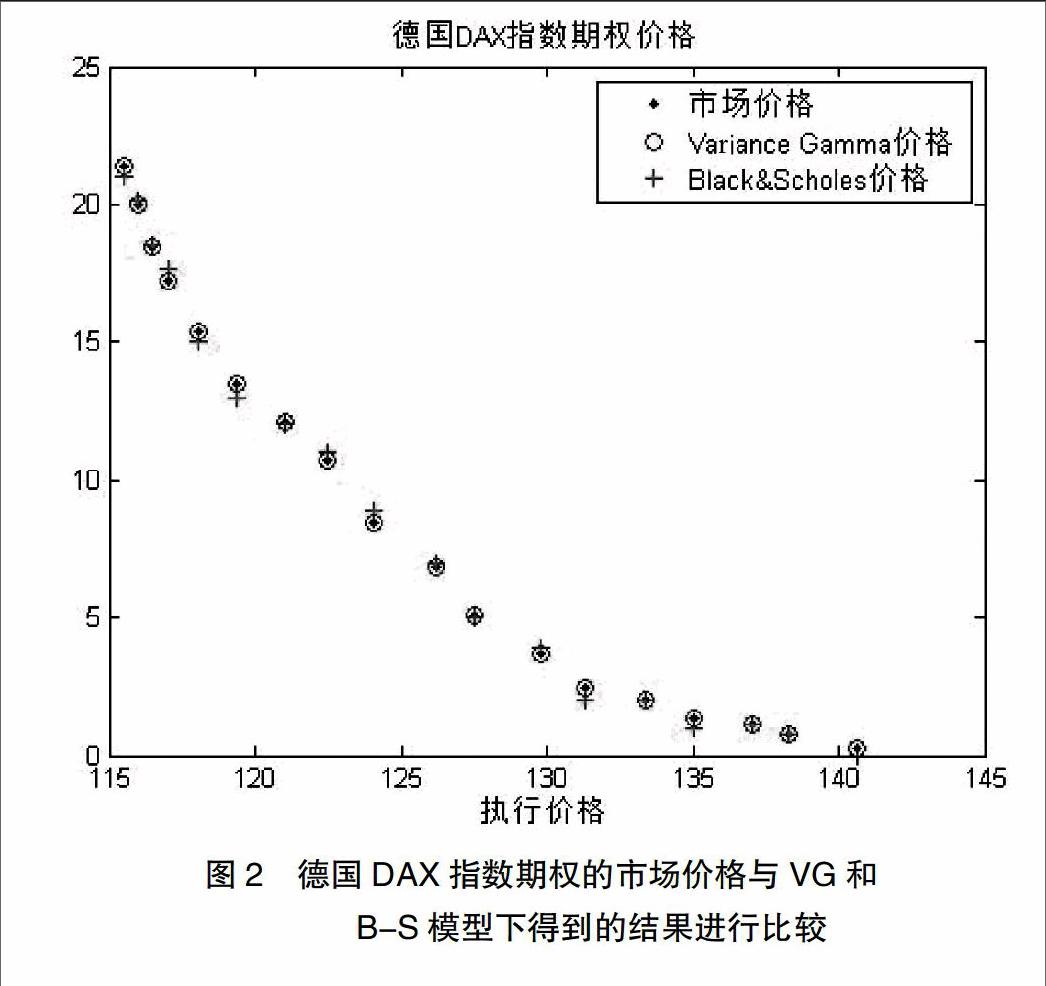
假定正态分布下，股票j的隐波动率记为σBLSj ，在VG模型下，VG隐波动率记为σVGj ，j=1，2，…，n。图2对B-S模型、VG模型和德国DAX指数交易的市场价格进行对比，可以观察到相比B-S模型，VG过程更能准确地捕捉到德国DAX指数分量的动态结构。

四、结论

经典的B-S模型是在完备市场下，假定一个连续变化的资产价格在未来任何时刻都服从对数正态分布，即假定资产的价格服从几何布朗运动，但更多的实证分析表明，金融市场存在着跳跃，资产收益率具有“尖峰厚尾”“波动聚集”“杠杆效应”等特征，而B-S模型不能对其进行准确描述。Lvy过程具有左极限右连续性质，能够描述数据分布的跳跃与偏峰特点，能够用小跳跃代替连续扩散。由于篮子资产间复杂的相依结构，使得一篮子期权在定价效率和精度上仍存在很大困难，故本文利用Lvy过程中接受度较高的VG过程，给出了一篮子期权在多维VG过程下的定价方法，并通过德国DAX指数作为现实数据进行检验，结果表明相比B-S模型，多维VG过程更能准确地拟合德国DAX指数期权，在期权定价领域具有优越性。

【参考文献】

[1] TANKOV P. Financial modelling with jump processes[M].CRC press，2003：64-94.

[2] MANDELBROT B B. The variation of certain speculative prices[J]. The Journal of Business，1963，36（4）：371-418.

[3] MADAN D B，SENETA E.The VG model for share market returns[J].The Journal of business，1990，63（4）：511-524.

[4] LUCIANO E， SCHOUTENS W. A multivariate jump-driven financial asset model[J]. Quantitative finance，2006，6（5）：385-402.

[5] KAAS R， DHAENE J， GOOVAERTS M J. Upper and lower bounds for sums of random variables[J]. Insurance：Mathematics and Economics，2000，27（2）： 151-168.

[6] VANDUFFEL S， HOEDEMAKERS T， DHAENE J. Comparing approximations for risk measures of sums of nonindependent lognormal random variables[J]. North American Actuarial Journal，2005，9（4）： 71-82.

[7] XU GUOPING， ZHENG H. Lower bound approximation to basket option values for local volatility jump-diffusion models[J]. International Journal of Theoretical and Applied Finance，2014，17（1）：1-15.

[8] 奚炜.VG期权定价模型的一种解析表达及评判检验[J].系统工程理论方法应用，2003（1）：49-52.

[9] 刘国光，王慧敏.基于纯粹跳跃利维过程的中外股票收益分布特征研究[J].数理统计与管理，2006（1）：43-46.

[10] 刘志东，陈晓静.无限活动纯跳跃Lvy金融资产价格模型及其CF-CGMM参数估计与应用[J].系统管理学报，2010（4）：428-438.

[11] RACHEV S T， MENN C， FABOZZI F J. Fat-tailed and skewed asset return distributions： implications for risk management， portfolio selection， and option pricing[M]. John Wiley & Sons，2005.

[12] Rosiski J. Tempering stable processes[J]. Stochastic processes and their applications，2007，117（6）：677-707.