精细积分法在结构碰撞中的应用研究

李传亮　王孟豪

(1.贵州省交通规划勘察设计研究院股份有限公司　贵阳　550081;　2.河南世纪博通工程咨询有限公司　郑州　450000)

精细积分法在结构碰撞中的应用研究

李传亮1王孟豪2

(1.贵州省交通规划勘察设计研究院股份有限公司贵阳550081;2.河南世纪博通工程咨询有限公司郑州450000)

摘要地震会引起相邻结构发生碰撞，导致结构损伤甚至倒塌。为更准确研究结构的碰撞问题及影响，文中将精细积分算法用于结构碰撞的求解中，并进行了公式推导和算例验证。结果表明，精细积分法对于结构的碰撞问题是适用的，并有无条件稳定、精度高和受时间步长限制小的优点。

关键词结构碰撞力学模型精细积分法积分步长

地面上相邻的结构动力特性若存在差异，在地震发生时会引起两结构的不同步振动[1-2]，从而导致碰撞，碰撞会对结构造成一定的损害[3]。对于地震作用引起的结构碰撞，碰撞作用力相当于突加荷载，需要做瞬态历程分析。目前采用的求解方法[4-5]是常用的隐式积分格式，将微分化成为差分算子，使得这些方法仅具有二阶精度或三阶精度，且对积分步长非常敏感，从而导致计算效率的降低。文献[6]采用具有四阶精度的Runge-Kutta法求解碰撞动力方程，但是对于高频振动计算容易发生不稳定和发散现象，而且计算所需的时间也相对比较长。

精细积分法是钟万勰教授于1994年提出，该方法从现代控制论的数学问题与结构力学问题互相模拟[7]，通过引入哈密顿体系中的对偶变量,对二阶的动力微分方程进行降阶,然后利用指数函数的精细算法得到高精度的解，可将逐步积分的计算精度极大提高，且受时间步长限制小。本文将其引入结构的碰撞问题求解中，通过结构碰撞的解析解算例，验证精细积分法的有效性和适用性。

1碰撞理论

图1为结构碰撞的力学模型，碰撞结构体系的动力平衡方程为

(1)

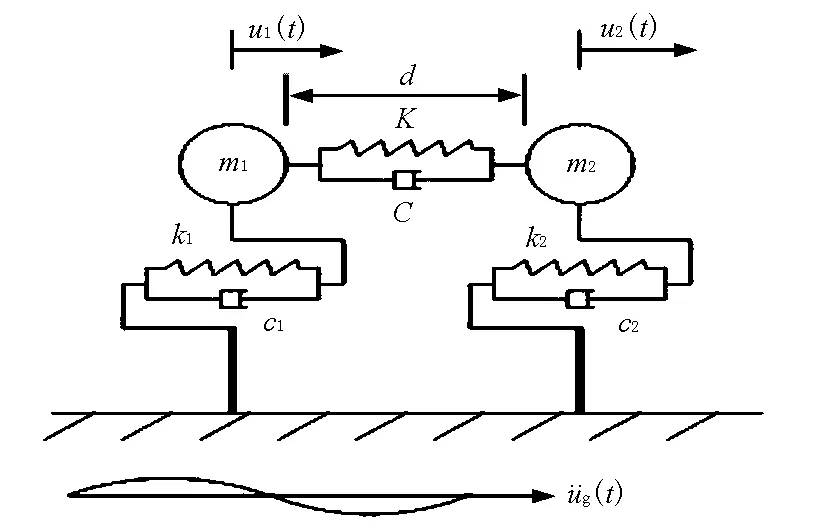
图1结构碰撞力学模型

2精细积分法求解碰撞问题

对式(1)采用精细积分法求解如下。

(2)

(3)

(4)

(5)

(6)

(7)

式(2)～(4)可化为

(8)

式(8)即为结构碰撞问题的状态传递方程。一般解为[8]

(9)

将荷载作用离散成步长Δt时间间隔，任意时刻表示kΔt为(k=0，1,2,…)，tk+1=tk+Δt，有

(10)

令T(Δt)=eHΔt

(11)

(12)

指数矩阵T(Δt)求解如下。

(13)

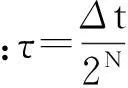
将指数矩阵展开为泰勒级数

(14)

(15)

式中:l为截断阶数。

若Ta与直接矩阵I相加后进行2N运算，会因计算机的舍入操作而丧失精度。为避免这一问题，式(14)计算过程如下。

(16)

计算得到(Ta)N，则

(17)

计算通过编程语言实现，求解过程为：

(2) 由式(12)得位移响应u1(tk)，u2(tk)。

(5) 重复以上(2)～(4)步骤，直至地震动输入完成，输出结果。

3算例验证

通过对2小球自由弹性碰撞进行模拟，图1中间隙d=0，2小球质量均为 2kg，自振角频率为10.25rad/s，初始时刻u1(0)=0.1 m,u2(0)=0m，左侧小球从初始位置向右侧自由运动与右侧小球发生弹性碰撞，假定碰撞过程中无能量损失，结构位移响应理论解见图2。

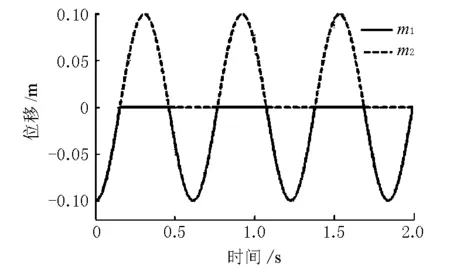
图2　位移响应理论解

3.1接触单元模型

算例假定碰撞过程中无能量损失，采用线性弹簧接触单元模型[9]模拟碰撞力。线性弹簧接触单元模型定义当2个结构间的相对位移大于伸缩缝间距时，碰撞弹簧发挥作用，在碰撞过程中产生碰撞力。线弹性模型加载和卸载过程的力-位移关系见图3，碰撞力的计算公式为

(18)

式中：d为伸缩缝初始间距；u1为1号结构位移；u2为2号结构位移；u2-u1为相对位移；F为碰撞力；kl为碰撞刚度。

a)　线弹性模型

b)　力-位移关系

3.2精细积分算法验证

采用精细积分法求解，积分步长0.000 2s，位移和碰撞力时程见图4～图5。分析发现，基于精细积分法求解的结构响应与理论解较为吻合；计算碰撞次数为6次，总体与理论相符，但是碰撞的位置随着时间推移出现差异，这是由于理论解满足动量守恒定律，但真实碰撞是在瞬间完成的，而采用线性弹簧接触模型的碰撞力总是有作用过程，这一过程随着接触弹簧刚度的增大而减小，其位移解也更接近理论解。

基于精细积分法求解的结构碰撞响应与文献[10]较为一致，但文献[10]采用隐式求解方法，积分步长为0.000 1s，是精细积分法积分步长的1/2，表明精细积分法选择较大积分步长也不影响其稳定性，因此计算效率也较高。

分析可知，精细积分法求解碰撞问题是有效和实用的，由式(14)和(15)，精细积分法理论上可以实现任何精度。

图4　基于精细积分法的位移解

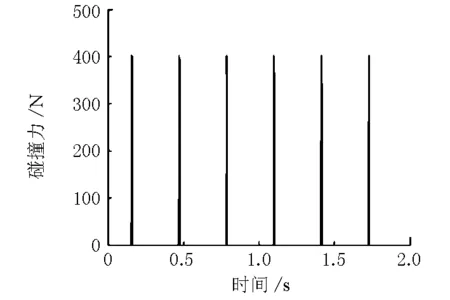
图5　基于精细积分法的碰撞力时程

4结语

精细积分法是一种显示积分方法，用于结构的碰撞响应分析，使求解具有高精度和高效率的特点。经算例验证，基于精细积分法推导的碰撞计算公式适宜于结构的碰撞研究与应用，理论上可实现任意精度，本文截断阶数取7也是合适的。

参考文献

[1]ANAGNOSTOPOULOSSA,SPILIOPOULOSKV.Aninvestigationofearthquakeinducedpoundingbetweenadjacentbuildings[J].Earthquakeengineering&structuraldynamics,1992,21(4):289-302.

[2]MAISONBF,KASAIK.Dynamicsofpoundingwhentwobuildingscollide[J].Earthquakeengineering&structuraldynamics, 1992, 21(9): 771-786.

[3]KASAIK,MAISONBF.Buildingpoundingdamageduringthe1989LomaPrietaearthquake[J].EngineeringStructures,1997,19(3):195-207.

[4]NEWMARKNM.Amethodofcomputationforstructuraldynamics[J].JournalofEngineeringMechanics,1959,85(3):249-260.

[5]WILSONEL.Nonlineardynamicanalysisofcomplexstructures[J].EarthquakeEngineeringandStructuralDynamics,1973(3):241-252.

[6]YAGHMAEI-SABEGHS,JALALI-MILANIN.Poundingfor-ceresponsespectrumfornear-fieldandfar-fieldearthquakes[J].ScientiaIranica,2012,19(5)：1236-1250.

[7]钟万勰.结构动力方程的精细时程积分[J].大连理工大学学报，1994,34(4):131-136.

[8]常春馨.现代控制理论基础[M].北京:机械工业出版社，1988.

[9]ZANARDOG,HAOH,MODENAC.Seismicresponseofmulti-spansimplysupportedbridgestoaspatiallyvaryingearthquakegroundmotion[J].EarthquakeEngineeringandStructuralDynamics,2002,31:1325-1345.

[10]ZHUP,ABEM,FUJINOY.Modellingthree-dimensionalnon-linearseismicperformanceofelevatedbridgeswithemphasisonpoundingofgirders[J].EarthquakeEngineering&StructuralDynamics,2002,31(11):1891-1913.

收稿日期：2014-09-30

ThePreciseIntegrationMethodintheApplicationofStructureImpactStudy

Li Chuanliang1,WangMenghao2

(1.GuizhouCommunicationsPlanningSurvey&DesignInstituteCo.,Ltd.,Guiyang550081,China；

2.HenanCenturyBoTongEngineeringConsultingCo.,Ltd.,Zhengzhou450000,China)

Abstract：Adjacent structures will collide with each other when the earthquake occur, resulting in structural damage even collapse, therefore the research of the collision problem of the structure is very important. In order to more accurately research the collision problems of the structure and its influence, in this paper, the precise integration algorithm is used to structure in the solution of the collision, and formula deduction and numerical example verification. The results show that the precise integration method for collision problem of the structure is applicable, and has the unconditional stability, high precision and restricted by time step of small advantages.

Key words:collision of the structure; mechanical model; precise integration method; integral step

DOI10.3963/j.issn.1671-7570.2015.01.039