基于正装迭代法的系杆拱吊杆张拉索力计算研究分析

徐治华　江　洲

(贵州省交通规划勘察设计研究院股份有限公司　贵阳　510085)

基于正装迭代法的系杆拱吊杆张拉索力计算研究分析

徐治华江洲

(贵州省交通规划勘察设计研究院股份有限公司贵阳510085)

摘要为了研究正装迭代法在索力计算中的应用，文中以某大桥(钢管混凝土系杆拱桥)的施工监控为工程背景，应用大型通用有限元软件Midas/Civil建立有限元模型对该桥进行施工阶段分析计算。采用正装迭代法对该桥施工阶段4次吊杆张拉的张拉控制力进行计算，用该结果指导施工，得出实测索力，将实测值与理论值进行对比分析。研究正装迭代法在钢管混凝土系杆拱桥索力计算中的应用。

关键词系杆拱吊杆索力正装迭代法

系杆拱又可称为简支梁拱组合体系。最近几年，系杆拱尤其是钢管混凝土拱桥在我国有较大的发展[1]。拱受压，梁受弯，这2种构件组合起来，使拱和梁各自的特点充分地发挥出来，用系杆平衡掉拱脚水平推力，从而降低对地基的要求，达到节省材料的目的。而在系杆和拱肋施工完毕之后，吊杆张拉是最关键的步骤。吊杆的主要作用是传递内力，所以，利用数值方法，根据施工阶段吊杆张拉顺序，确定施工中吊杆的张拉控制力，使该阶段吊杆施工张拉完毕后，所有吊杆索力均达到设计值，吊杆不必要返回张拉调整，这样可大量缩短施工时间和节省施工费用。

1工程实例

某大桥为钢管混凝土结构，采用刚性系梁刚性拱，计算跨径L=115 m，拱轴线为二次抛物线，矢跨比为1/5,矢高23 m。拱肋采用哑铃形钢管混凝土，截面高度为280 cm，每个钢管外径120 cm,钢管及腹板壁厚1.4 cm，内充C50微膨胀混凝土；风撑采用改良X形撑，由壁厚1.6 cm钢管焊接而成，全桥共5组；吊杆采用外径9.3 cm的成品拉索，每片拱肋设吊杆21根，间距为510 cm。桥梁结构照片见图1。

施工流程如下：下部基础施工→支架现浇系梁、横梁、桥面板→张拉系梁及中横梁第1批预应力束→拱肋架设并安装横撑→泵送混凝土→安装吊杆并进行第1次张拉→张拉系梁第2批预应力束→拆除系梁施工支架→吊杆进行第2次张拉→张拉系梁第4批预应力束并安装行车道板→吊杆进行第3次张拉→张拉系梁第4批钢束及中横梁剩余的全部预应力束→沥青铺装并安装护栏等附属结构。

图1　某大桥照片

该桥共进行3次吊杆张拉，每次均应对称张拉，相同编号的4根吊杆应同时张拉，每次控制索力严格按照设计要求进行张拉。第1次在泵送完钢管混凝土之后进行张拉，目标控制索力390 kN；第2次在拆除所有支架后进行，目标控制索力为820 kN;第3次在安装完桥面板后进行张拉，目标控制索力 1 220 kN。3次张拉结束后进行桥面混凝土现浇。

2吊杆张拉计算方法

桥梁施工过程按照预先设定的施工步骤，安全地达到成桥状态，且成桥状态与理想的成桥状态吻合，将该施工过程称为施工阶段合理的设计状态。要达到合理的成桥吊杆索力，在施工过程中，吊杆要分多次张拉，在这个过程中，结构支承体系的变化，会引起结构内力的重新分布，钢管混凝土系杆拱桥是一个外部静定而内部高次超静定的结构，在张拉吊杆的过程中，后张拉的吊杆张拉时会引起已张拉吊杆的索力发生变化，而已张拉的吊杆也会对后张拉的吊杆的索力产生影响，所以在整个张拉过程中，除了最后张拉的一组吊杆，其他的一直都处于变化的状态。所以就需要对施工过程的吊杆张拉控制力进行计算，获取一组张拉索力来保证张拉结束后，所有的吊杆索力正好达到目标控制力。所以，施工阶段关于吊杆张拉的一个关键问题就是计算吊杆的张拉控制力。而目前普遍采用的方法就是正装迭代法[2]。本桥也采用此方法。

采用midas civil 2012建立空间有限元模型，进行吊杆张拉方案设计。如图2所示，全桥共划分532个节点，1 378个单元，吊杆采用桁架单元(仅受拉)，其余构件采用梁单元模拟[3]。

图2　有限元模型

正装法应用于吊杆索力计算的基本方法为: 首先假定一组初始索力,然后进行一次正装计算,得到一组成桥状态时的索力，将该组索力与目标索力进行对比求出两者差值,得到最新的安装索力,再进行新的一轮正装计算,直至收敛为止。具体步骤如下。

第1步。输入桥梁结构基本参数。

第2步。架设成桥索力为F0，第i次迭代计算时输入的初始索力为Fi，相应的计算结果索力为F。

第3步。结合有限元软件，令Fi=F0进行第一次迭代计算，求得吊杆索力F。

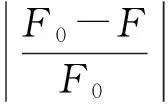
本文以第2次吊杆张拉为例，采用正装迭代法计算张拉控制力，结果见表1。

表1　吊杆第2次张拉张拉控制力计算结果

施工单位严格按照表1所列的张拉顺序及张拉控制力进行施工，每根吊杆均张拉到位，在张拉过程中，其他施工工作均停止进行。完成张拉之后用索力仪对各个吊杆索力进行了测量，最后得到的实测结果与理论值对比见表2，图3。

表2　某大桥实测索力与目标索力对比

注：1.该桥X，S侧各21根吊杆；2.桥梁纵向对称吊杆相同编号。

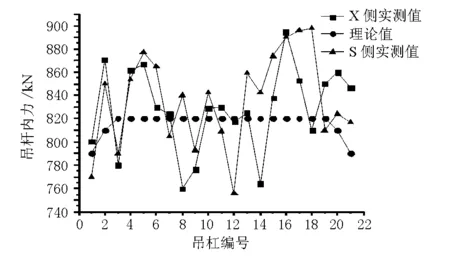
图3　第二次吊杆张拉索力实测值与理论值对比图

由表2及图3可见，某大桥X侧吊杆实测索力比较均匀，与目标索力相差不大，误差均控制在10%以内；S侧吊杆实测索力比较均匀，与目标索力相差不大，误差均在10%以内，结果良好。由以上结果分析得出，该次正装迭代法计算所得的张拉控制力较好地指导了施工，结构内力与设计基本吻合，达到了预期的效果，结构在该阶段施工过程中处于安全状态。对于短吊杆，由于其刚度比较大，采用频率法测试吊杆力，误差较大，此时测量数据不可信，可按实测千斤顶读数校验[4]。

3结论

(1) 某大桥在4次张拉结束后，实测值与理论值误差均控制在10%以内，成功地达到了目标索力，从而使结构达到成桥索力，在张拉过程中，结构实测索力与理论计算索力基本吻合。

(2) 采用正装迭代法计算的施工阶段吊杆张拉控制力能够很好地指导施工，使张拉结果达到目标控制力，误差在规范要求范围之内。

(3) 正装迭代法的迭代次数较多，当单元数量较多时，迭代时间较长。

参考文献

[1]严志刚，盛洪飞.钢管混凝土拱桥的发展优势[J].东北公路，2002,25 (1):31-33.

[2]朱小秀.正装迭代法在系杆拱桥吊杆张拉过程中的应用[J].城市道桥与防洪,2010(1):49-53.

[3]于琦,孟少平.系杆拱桥吊杆张拉控制有限元模拟方法研究[J].特种结构,2008,25(1):88-90.

[4]唐小军,王道波,唐得志,等.虚拟参考反馈校正控制器参数的预测误差辨识[J].华南理工大学学报：自然科学版,2013(5):33-34.

收稿日期：2014-11-05

DOI 10.3963/j.issn.1671-7570.2015.01.006