双调和Abel-Poisson算子对Hölder函数类的逼近
2016-01-06有名辉
双调和Abel-Poisson算子对Hölder函数类的逼近
有名辉
(浙江机电职业技术学院数学教研室,杭州310053)
[摘要]建立了双调和Abel-Poisson算子对Hölder函数类的逼近度的渐进等式,解决了双调和Abel-Poisson算子和Hölder函数类的Kolmogorov-Nikol’skii 问题.
[关键词]双调和Abel-Poisson算子; Hölder函数类; 逼近; 渐进等式; Kolmogorov-Nikol’skii问题
[收稿日期]2015-03-20;[修改日期]2015-05-15
[中图分类号]O174.42[文献标识码]A
1引言
记C2π是周期为2π的连续函数的全体,对f∈C2π定义范数:
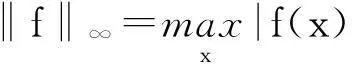
若f∈C2π满足不等式
‖f(x+h)-f(x)‖∞≤|h|α(0<α≤1),
(1)
则称f(x)满足Hölder条件,满足条件(1)的函数的全体称为Hölder函数类,记为Hα.
若f∈C2π满足不等式
‖f(x+h)-2f(x)+f(x-h)‖∞≤2|h|α(0<α≤2,|h|≤2π),
(2)
则称f(x)满足Zygmund条件,满足条件(2)的函数的全体称为Zygmund函数类,记为Zα.
对于C2π中的可积函数f,定义双调和Abel-Poisson积分A2(f,r,x)如下:
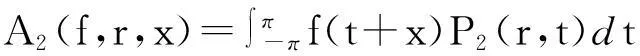
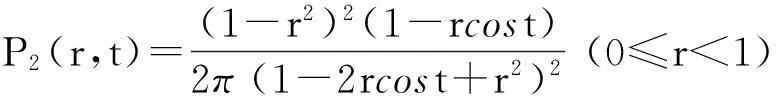
考查双调和Abel-Poisson积分算子对某一函数类K的逼近度,通常用量
(3)
来表示.如果存在函数φ(1-r)=φ(K;A2(f,r,x);(1-r))满足:
E(K,r)=φ(1-r)+o(φ(1-r))(r→1-0),
则称算子A2(f,r,x)和函数类K的Kolmogorov-Nikol’skii 问题[3]解决了.
上个世纪60年代,Kaniev[4],Pych[5]研究了K=H1的情形,并取得了一定的成果.如1968年,Pych[5]建立了如下渐进等式
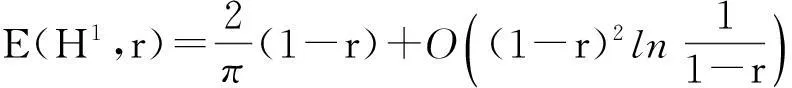
2000年, Zhigallo和Kharkevych[6]把Pych的结果进行了如下推广:
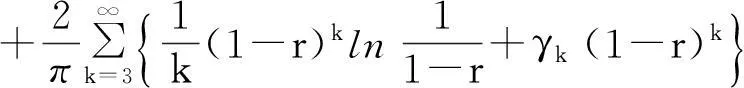
其中
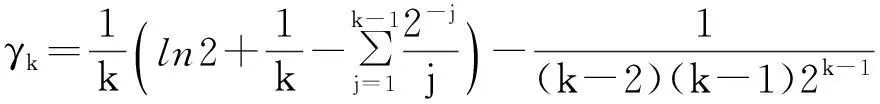
对于K=Hα(0<α<1)的情形,近些年来,一直未见相关研究成果出现.本文在此主要研究双调和Abel-Poisson算子对Hölder函数类Hα(0<α<1)的逼近.
2主要结果
定理1设0<α<1,E(Hα,r)如式(3)定义,则r→1-0时,有如下渐进等式:
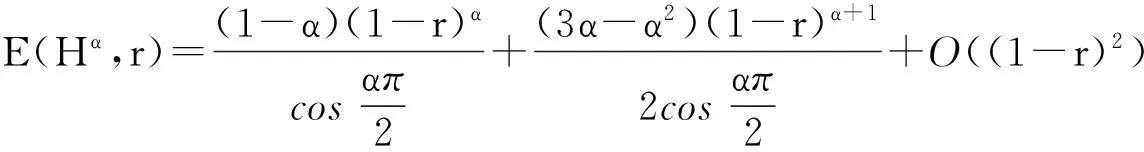
(4)
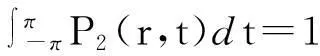
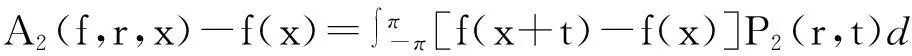
因此,利用式(1), 即得
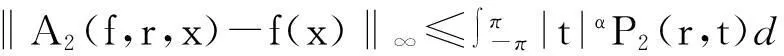
(5)
显然|t|α∈Hα,并且
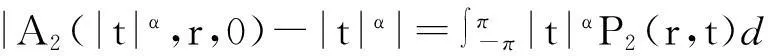
(6)
结合式(3),(5)及(6)可得
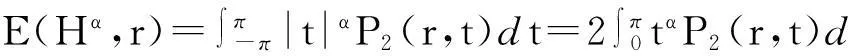
(7)
记
∶=I1+I2.
(8)
经过简单的计算,不难得到
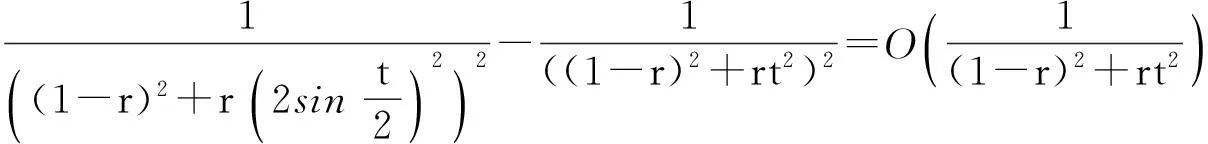
(9)
结合式(9),可知
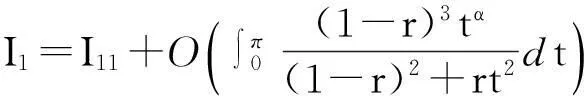
(10)
其中
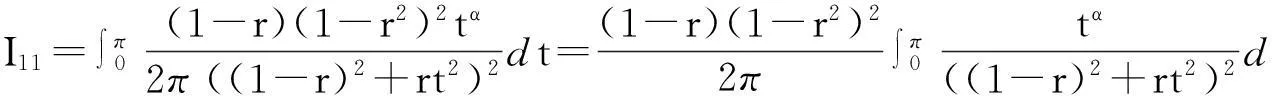
(11)
利用变量代换,可得
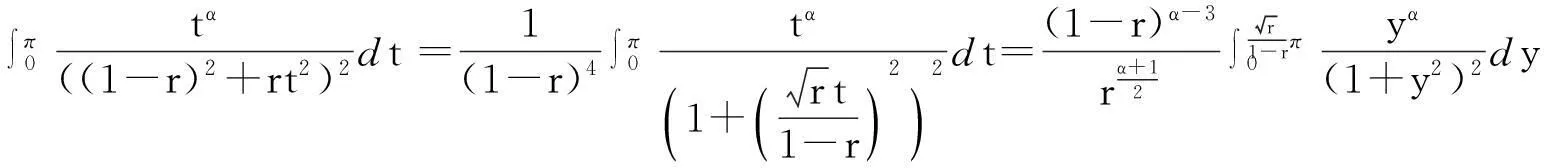
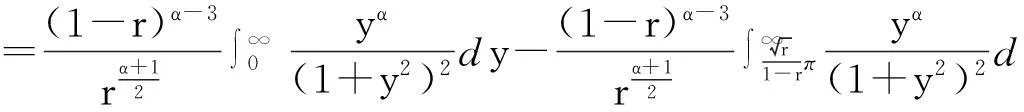
(12)
利用β函数和Γ函数[7]的性质,可得
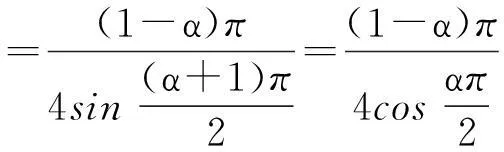
(13)
同时,不难证明
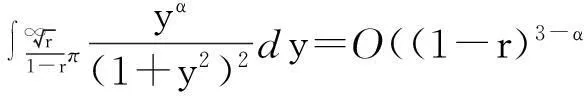
(14)
再把式(13),(14)代入到式(12),可得
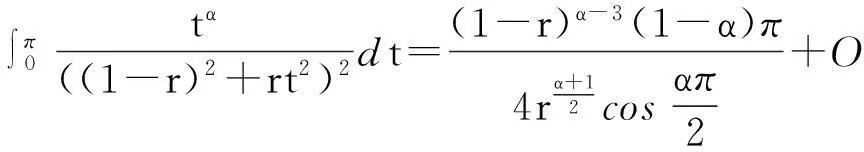
(15)
把式(15)代入到式(11),便得
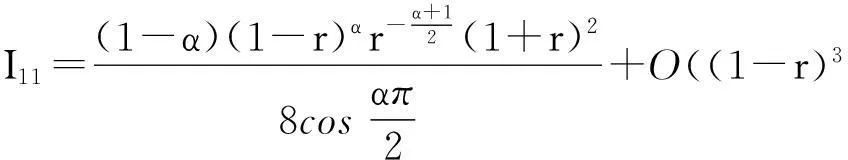
(16)
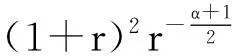
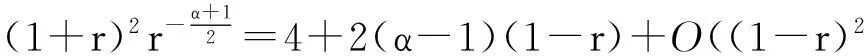
(17)
结合式(16),(17),则有
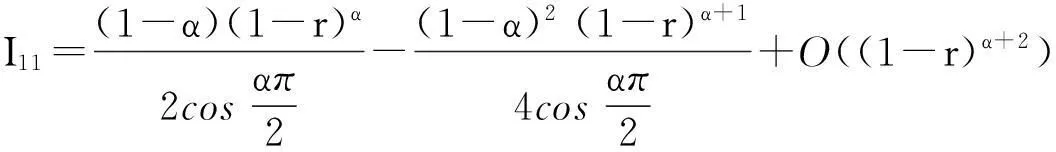
(18)
考查式(10)中的积分,经过细致的计算,不难算得
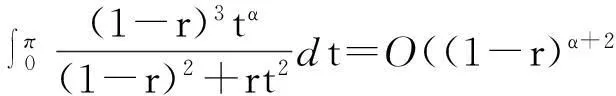
(19)
把式(18),(19)代入式(10),可知
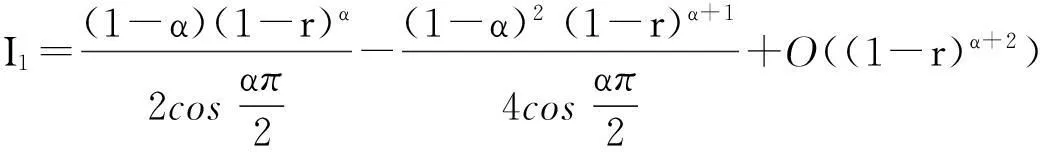
(20)
以下考查式(8)中的I2,经过简单而细致的计算,可得
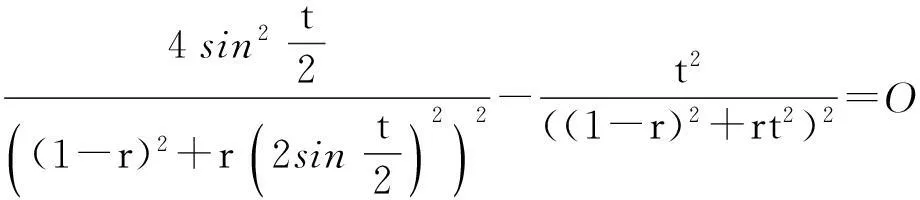
(21)
利用式(21),易得
I2=I21+O((1-r)2),
(22)
其中
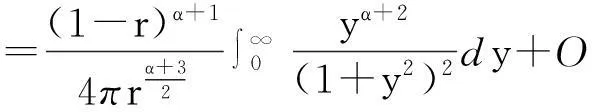
(23)
再次利用β函数和Γ函数的性质,可以算得
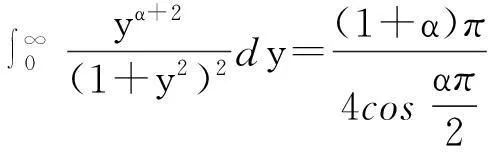
(24)
把式(24)代入到式(23),并结合式(22),得
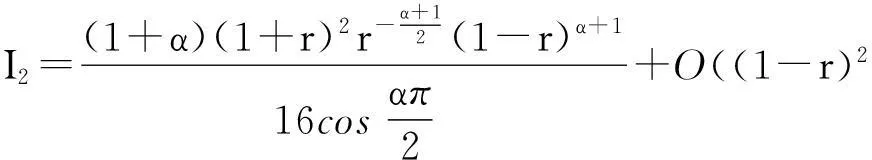
(25)
结合式(17)和式(25),可知
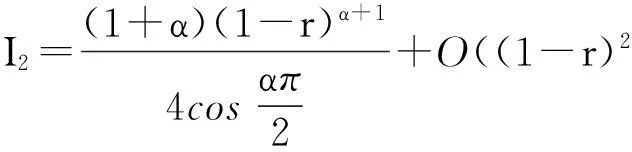
(26)
把式(20)、(26)代入到(8),并结合式(7),便得
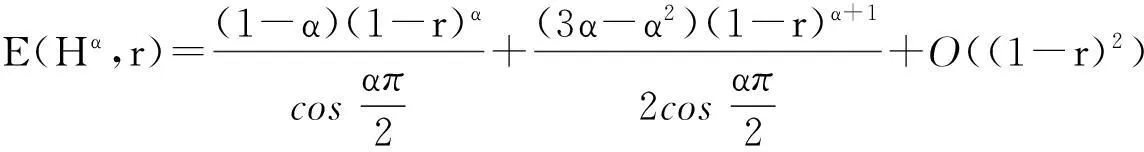
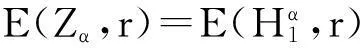
推论1设0<α<1,E(Zα,r)如式(3)定义,则r→1-0时,有如下渐进等式:
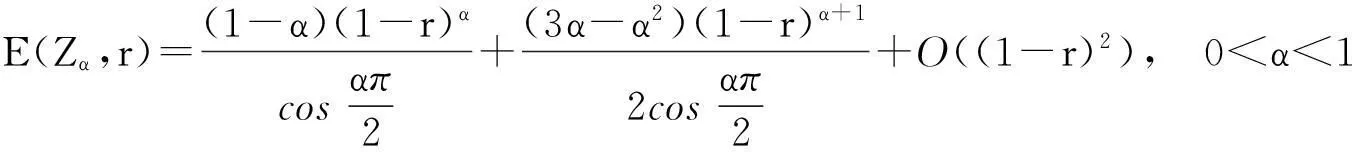
[参考文献]
[1]Tikhonov A N . Samarskii A A. Equations of Mathematics Physics [M]. Moscow: Nauka, 1977.
[2]Petrov V A. Biharmonic Poisson integral[J]. Lit. Mat. Sb., 1967, 7(1): 137-142.
[3]Stepanets A I. Classification and approximation of periodic function by its Poisson integral[J]. Dokl. Akad. Nauk SSSR, 1950, 74:17-20.
[4]Kaniev S. On the deviation of functions biharmonic in a disk from their boundary values[J]. Dokl. Akad. Nauk SSSR, 1963, 153(5): 995-998.
[5]Pych P. On a biharmonic function in unit disk[J]. Ann. Pol. Math, 1968, 20(3): 203-213.
[6]Zhigallo K M, Kharkevych Yu I. On the approximation of functions of the Hölder class by biharmonic Poisson integrals[J]. Ukr. mat. zh., 2000, 52(7): 1113-1117.
[7]Γ.M.菲赫金哥尔茨.微积分学教程(第二卷)[M].北京:高等教育出版社,2006.
On the Approximation of Functions of the Hölder Class by
Biharmonic Abel-Poisson Integral
YOUMing-hui
(Mathematics Teaching and Research Section,Zhejiang Institute of Mechanical and Electrical Engineering,
Hangzhou 310053, China)
Abstract:This paper establishes the asymptotic equality of the upper bound of the deviation of the biharmonic Abel-Poisson integral from functions of the Hölder class, and solves the Kolmogorov-Nikol’skii problem of the biharmonic Abel-Poisson integral and the functions of the Hölder class.
Key words: approximation; biharmonic Poisson integral; Hölder class; asymptotic equality; Kolmogorov-Nikol’skii problem
