一元h-F凸函数的导数判别法
2016-01-06时统业,万福,丁霞
一元h-F凸函数的导数判别法
时统业,万福,丁霞
(海军指挥学院信息系,南京211800)
[摘要]利用h-F凸函数的定义,在h满足一定条件的情况下,导出满足条件P1,P2的h-F凸函数的等价条件.
[关键词]h-F凸函数; 等价条件; 可导函数
[收稿日期]2015-03-09
[中图分类号]O178[文献标识码]C
1引言
定义1[1]称集合K⊂n是关于F的广义凸集,若存在向量值映射F∶K×K×[0,1]→n,使得∀λ∈[0,1],∀x,y∈K,有F(x,y,λ)∈K.
与广义凸集有关的文献可见[1-8].
定义2[2]设K⊂n是关于F的广义凸集,称F在K上满足条件P1,P2,若∀α,β∈[0,1],且α<β,∀x,y∈K,有
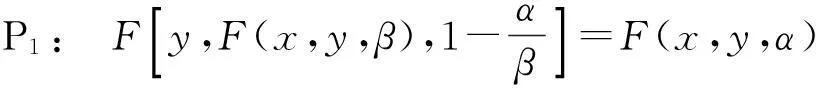
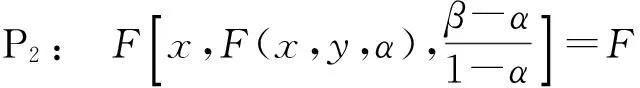
定义3[3]设K⊂n,J⊂,[0,1]⊂J.h∶J→[0,+∞)且h不恒为零,集合K⊂n是关于F的广义凸集,称f∶K→[0,+∞)在K上是h-F凸函数,若∀λ∈[0,1],∀x,y∈K,有
f[F(x,y,λ)]≤h(λ)f(x)+h(1-λ)f(y).
在定义3中,若
F(x,y,λ)=λx+(1-λ)y,h(λ)=λ,
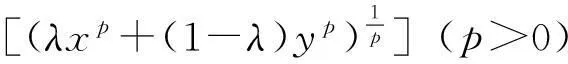
本文的目的是当F在K上满足条件P1, P2,h满足一定条件,F(x,y,λ)是[0,1]上关于λ的连续函数,f(F(x,y,λ))是[0,1]上关于λ的可导函数,给出h-F凸函数的等价条件.
2主要结果
定理1设K⊂是关于F的广义凸集,F在K上满足条件P1,[0,1]⊂J⊂.h∶J→[0,+∞)满足h(0)=0,h(1)=1,且h′+(0)和h′-(1)存在.对任意x,y∈K,F(x,y,λ)是[0,1]上关于λ的连续函数,f(F(x,y,λ))是[0,1]上关于λ的可导函数.若f∶K→[0,+∞)在K上是h-F凸函数,则对任意x,y∈K,α∈[0,1],有
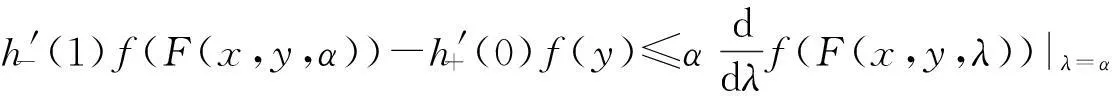
(1)
证因为f在K上是h-F凸函数,F在K上满足条件P1,所以对任意x,y∈K,α,β∈[0,1],α<β,有
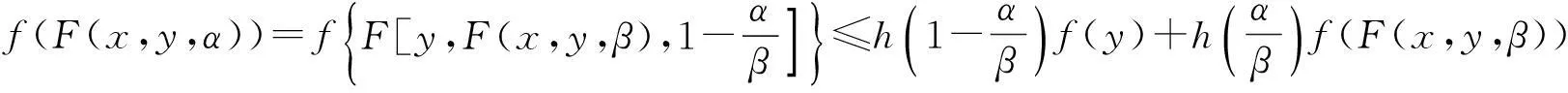
由此得
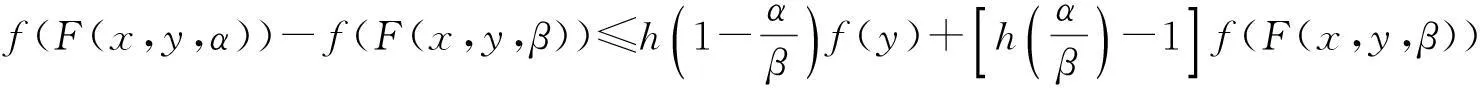
(2)
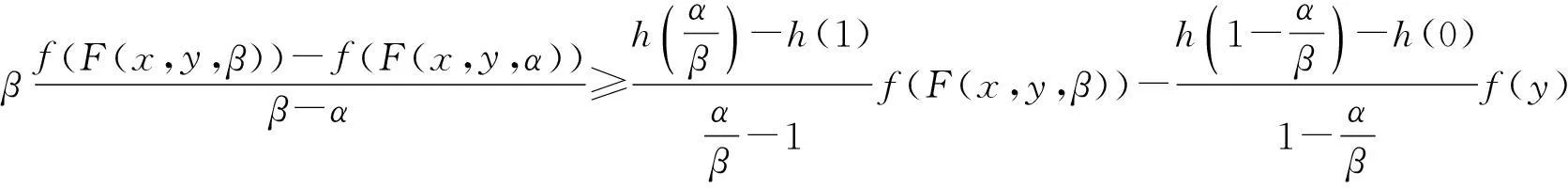
(3)
在式(3)中,令β→α+0,得
对任意α∈[0,1)成立.在式(3)中,令α→β-0,得
对任意β∈(0,1]成立.综上所述,对任意α∈[0,1],式(1)成立.
定理2设K⊂是关于F的广义凸集,F在K上满足条件P2,[0,1]⊂J⊂.h∶J→[0,+∞)满足h(0)=0,h(1)=1,且h′+(0)和h′-(1)存在,对任意x,y∈K,F(x,y,λ)是[0,1]上关于λ的连续函数,f(F(x,y,λ))是[0,1]上关于λ的可导函数.若f∶K→[0,+∞)在K上是h-F凸函数,则对任意x,y∈K,α∈[0,1),有
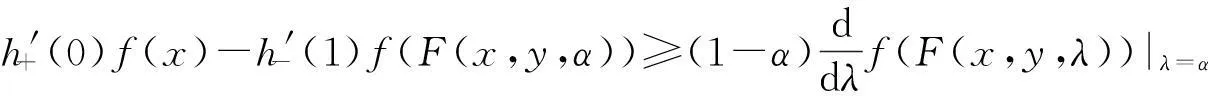
(4)
证因为f在K上是h-F凸函数,F在K上满足条件P2,所以对任意x,y∈K,α,β∈[0,1],α<β,有
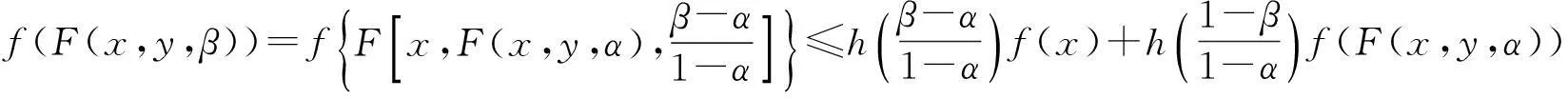
由此得
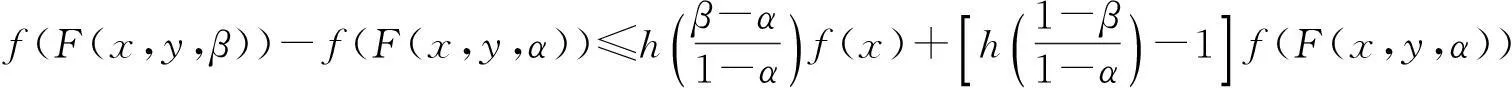
(5)
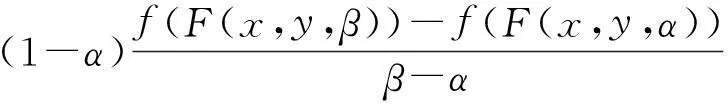
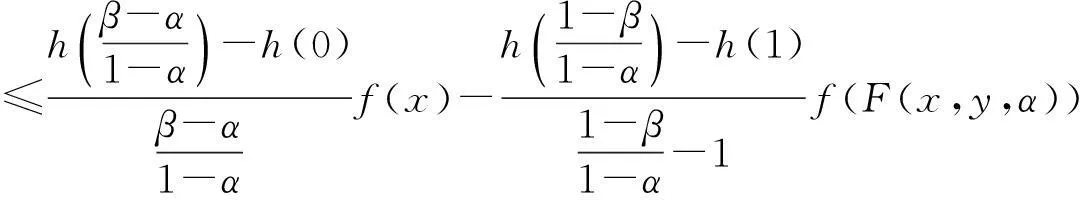
(6)
在式(6)中,令β→α+0得式(4)对任意α∈[0,1)成立.
定理3设K⊂是关于F的广义凸集,F在K上满足条件P1,[0,1]⊂J⊂.h∶J→[0,+∞),h′+(0)和h′-(1)存在,对任意x,y∈K,f(F(x,y,λ))是[0,1]上关于λ的可导函数.若对任意x,y∈K,α∈(0,1),式(4)成立,则有式(1)成立.
证由式(4)可知,对任意x,y∈K,α∈(0,1),有
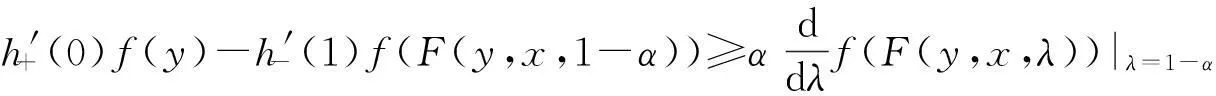
(7)
在式(7)中,以F(x,y,1)替代x,则由条件P1,对任意α∈(0,1),F(y,x,1-α)化为
F(y,F(x,y,1),1-α)=F(x,y,α),
而对任意λ∈(0,1],F(y,x,λ)化为
F(y,F(x,y,1),λ)=F(x,y,1-λ),
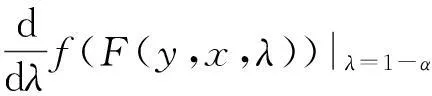
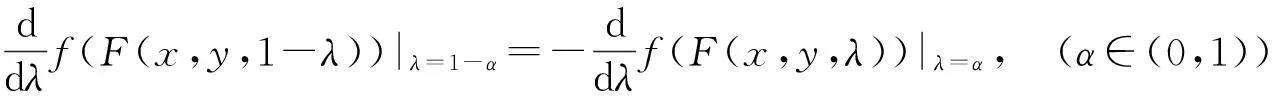
于是式(7)化为式(1).
定理4设K⊂是关于F的广义凸集,F在K上满足条件P1,[0,1]⊂J⊂.h∶J→[0,+∞),对任意x,y∈K,f(F(x,y,λ))是[0,1]上关于λ的可导函数.若对任意x,y∈K,α∈(0,1),式(1),(4)成立,则对任意x,y∈K,α∈(0,1),有
f(F(x,y,α))≤h(α)f(x)+h(1-α)f(y).
(8)
证式(4)即
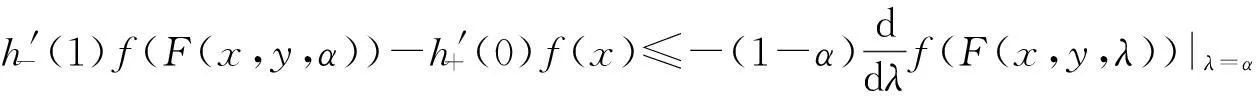
(9)
式(9)和式(1)分别乘以1-α和α,然后相加得
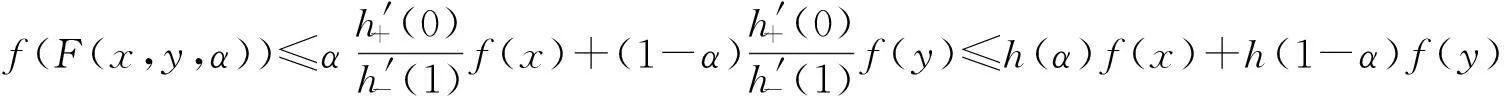
式(8)得证.
定理5设K⊂是关于F的广义凸集,F在K上满足条件P1,[0,1]⊂J⊂.h∶J→[0,+∞),h′+(0)和h′-(1)存在,对任意x,y∈K,f(F(x,y,λ))是[0,1]上关于λ的可导函数.若对任意x,y∈K,α∈[0,1],式(1)成立,则对任意x,y∈K,α∈(0,1),有
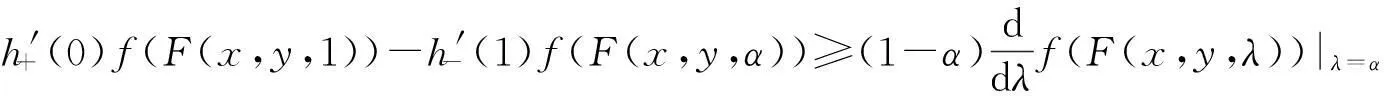
(10)
证由式(1)可知,对任意x,y∈K,α∈[0,1],有
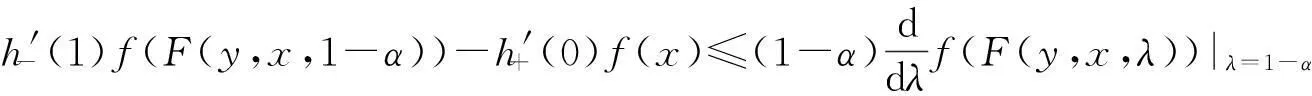
(11)
在式(11)中,以F(x,y,1)替代x,则由定理3的证明可知,当α∈(0,1)时,式(11)化为
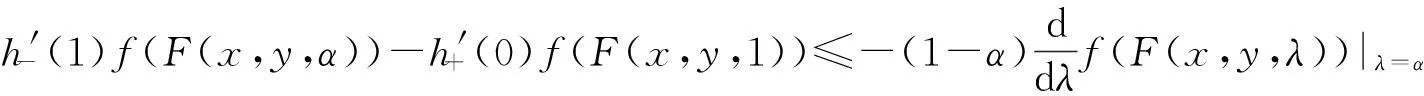
也即式(10)成立.
定理6设K⊂是关于F的广义凸集,F在K上满足条件P1,[0,1]⊂J⊂.h∶J→[0,+∞)满足h(0)=0,h(1)=1,且h′+(0)>0,h′-(1)>0,对任意α∈[0,1]有
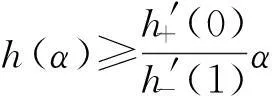
对任意x,y∈K,F(x,y,λ)是[0,1]上关于λ的连续函数,f(F(x,y,λ))是[0,1]上关于λ的可导函数,则下面命题等价:
(i)f在K上是h-F凸函数;
(ii) 对任意x,y∈K,α∈[0,1],式(1)成立,且有
f(F(x,y,1))≤f(x),f(F(x,y,0))≤f(y);
(iii) 对任意x,y∈K,α∈(0,1),式(4)成立,且有
f(F(x,y,1))≤f(x),f(F(x,y,0))≤f(y).
证(i)⟹(ii).由定理1得证.
(ii) ⟹ (iii).若对任意x,y∈K,α∈[0,1],式(1)成立,则由定理5,对任意x,y∈K,α∈(0,1),式(10)成立.又因f(F(x,y,1))≤f(x),h′+(0)>0,故对任意x,y∈K,α∈(0,1),式(4)成立.
(iii) ⟹ (i).若对任意x,y∈K,α∈(0,1),式(4)成立,则由定理3知,对任意x,y∈K,α∈(0,1),式(1)也成立.再由定理4知对任意x,y∈K,α∈(0,1),有式(8)成立.又因
f(F(x,y,1))≤f(x),f(F(x,y,0))≤f(y),
故式(8)对α=0和α=1都成立,由定义知f在K上是h-F凸函数.
推论6.1设f(x)是[a,b]⊂(0,∞)上的可导函数,则f∶[a,b]→[0,+∞)在I上是h凸函数当且仅当对任意y,z∈[a,b],y≠z,有
h′-(1)f(z)-h′+(0)f(y)≤(z-y)f′(z).
(12)
证根据定理6,只需证明当F(x,y,λ)=λx+(1-λ)y时,式(1)与式(12)等价.事实上,若式(12)成立,取z=αx+(1-α)y并注意到
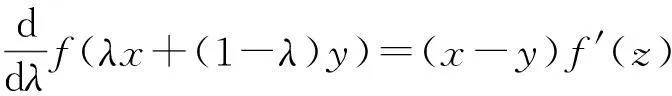
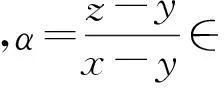
与推论6.1的证明类似,还可证明下面的推论6.2和推论6.3.
推论6.2设f(x)是[a,b]⊂(0,∞)上的可导函数,则f∶[a,b]→[0,+∞)是h-GA凸函数当且仅当对任意y,z∈[a,b],y≠z,有
h′-(1)f(z)-h′+(0)f(y)≤zf′(z)(lnz-lny).
推论6.3设f(x)是[a,b]⊂(0,∞)上的可导函数,则f∶[a,b]⊂(0,∞)→[0,+∞)在[a,b]上是h-p凸函数当且仅当对任意y,z∈[a,b],y≠z,有
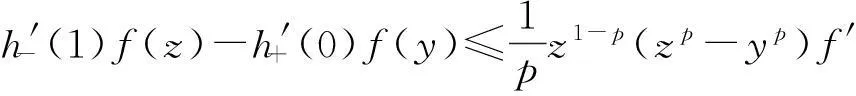
[参考文献]
[1]黄金莹,赵宇,方秀男.F-G广义凸函数与拟凸函数[J].重庆师范大学学报(自然科学版),2011,28(4):11-15.
[2]黄金莹,赵宇.广义凸函数的Hadamard不等式[J].重庆师范大学学报(自然科学版), 2013,30(4):1-5.
[3]王国栋.h-F凸函数的一类Hadamard不等式[J].重庆师范大学学报(自然科学版), 2014,31(6):1-4.
[4]康兆敏,赵宇,方秀男.F-G广义凸函数的若干性质[J].贵州师范大学学报(自然科学版),2011,29(2):72-76.
[5]黄金莹,赵宇.广义凸函数与弱近似凸集[J].黑龙江大学学报(自然科学版),2011,28(2):200-205.
[6]赵宇,黄金莹.半严格F-G广义凸函数[J].重庆师范大学学报(自然科学版),2011,28(1):7-12.
[7]赵宇,黄金莹,康兆敏.广义凸函数的特征性质[J].大学数学,2011,27(6):105-110.
[8]时统业,焦寨军,周国辉.F-G广义凸函数的一个性质及其应用[J].贵州师范大学学报(自然科学版),2012,30(5):41-45.
[9]Varošanec S.Onh-convexity[J].J Math Anal Appl,2007,326(1):303-311.
Derivation Diagnostic Method of h-F-Convex
Functions of One Variable
SHITong-ye,WANFu,DINGXia
(Department of Information, PLA Naval Command College,Nanjing 211800, China)
Abstract:With the aid of the definition of h-F-convex functions,several equivalent conditions of h-F-convex functions satisfying condition P1,P2 are obtained when h satisfying certain conditions.
Key words:h-F-convex function; equivalent condition; differentiable function
