同步坐标下无刷双馈电机无源性控制
2016-01-06陈集思,杨俊华,黄健健等
同步坐标下无刷双馈电机无源性控制*
陈集思1,杨俊华1,黄健健2,吴捷3
(1. 广东工业大学 自动化学院,广东 广州510006;
2. 机械工业部深圳设计研究院有限公司,广东 深圳518000;
3. 华南理工大学 电力学院,广东 广州510641)
摘要:针对无刷双馈电机非线性PID控制方案中转速和负载转矩动态响应性能差,负载突变时易引起振荡等问题,提出无源性控制策略。根据无刷双馈电机同步速旋转坐标系下的电压、磁链和转矩方程,建立电机的欧拉-拉格朗日模型;从能量角度分析电机电气子系统与机械子系统的无源性,设计电机的转矩控制器和转速控制器。为改善系统动态响应,降低其对参数变化的灵敏度,通过在控制器中加入非线性阻尼,实现系统的快速收敛。基于MATLAB/Simulink环境搭建了无刷双馈电机无源性控制的仿真模型,仿真结果表明,无源性控制策略可快速跟踪给定转速,动态响应性能好,全局稳定、鲁棒性好。
关键词:无刷双馈电机; 无源性控制; 非线性阻尼; 动态响应; 鲁棒性
基金项目:* 国家自然科学基金资助项目(51307025,5177050,51407035);广东省高等学校科技创新项目(2013KJCX0059);广东高校优秀青年创新人才培养计划项目资助(2012LYM_0052;2013LYM_0019)
通讯作者:陈集思
中图分类号:TM 301.2;TP 273文献标志码: A
收稿日期:2015-03-26
Passivity-Based Control Strategies of Brushless Doubly-Fed Machine
CHENJisi1,YANGJunhua1,HUANGJianjian2,WUJie3
(1. School of Automation, GuangdongUniversity of Technology, Guangzhou 510006, China;
2. Shenzhen Machinery Institure Architectural Design, Co., Ltd., Shenzhen 518000, China;
3. School of Electric Power, South China University of Technology, Guangzhou 510641, China )
Abstract:A novel passive control strategy was proposed to improve the dynamic response performance of the speed and load torque of the brushless doubly-fed machine(BDFM) with the nonlinear PID control scheme,and the oscillation as the load changes suddenly. The Euler-Lagrangian model of BDFM was established based on the equations of the voltage,flux and torque of BDFM in synchronous speed rotary coordinate system. The passivity of the electrical subsystems and mechanical subsystems of the machine were analysized by the view of energy, and the controllers of the torque and speed were designed.In order to improve the system dynamic response and reduce its sensitivity to parameter variations, the nonlinear damping was added into the controller to make the system achieve fast convergence.A novel simulation model of BDFM with passivity control strategy was built in MATLAB/Simulink environment.The simulation results showed that a given speed of BDFM could be fastly tracked, BDFM had good dynamic performance,global stability and good robustness with the passive control strategy.
Key words: brushless doubly-fed machine; passivity based control; nonlinear damping; dynamic response; robustness
0引言
无刷双馈电机(Brushless Doubly-Fed Machi-nes, BDFM)是一种新型交流调速电机。BDFM结构简单稳固、功率因数可调、调速控制装置容量小、运行模式灵活,在可调速驱动系统和变速恒频发电领域应用前景广泛。近年来,国内外学者对BDFM进行了较多研究,建立了较为准确实用的数学模型[1],提出标量控制[2]、矢量控制[3]、转子磁场定向控制[4]、直接转矩控制[5-9]、智能控制[10-12]、自适应控制[13-15]等多种控制策略。文献[4]分别将BDFM的功率绕组和控制绕组在各自的同步坐标系下进行磁场定向,数学模型和转子磁场定向控制策略得以简化,控制性能良好。文献[5]研究了一类无刷双馈电机直接转矩控制系统,结构简单、计算量小,但磁链和转矩脉动较大。为此,文献[7]提出采用转矩预测法,有效减小了转矩脉动并改善了定子电流波形。文献[10]通过引入转矩预测控制策略,获得了良好的动态性能。采用磁场定向矢量控制方案的BDFM调速系统,存在超调及动态稳定迟滞等问题,文献[11]结合模糊控制和PI控制,控制效果明显好于单独的PI控制。文献[12]设计了BDFM的PID神经网络控制器,转速跟踪准确,但过分依赖于系统模型,对系统未建模动态和未知扰动亦未作出较好的估计和补偿。基于波波夫超稳定性理论的模型参考自适应算法,文献[13]提出了一种转矩和磁链计算的新方法,改进了BDFM直接转矩控制策略。BDFM是一个高阶、多变量、非线性及强耦合系统,各类控制策略都存在局限性[16]。
无源性控制策略(Passivity Based Control, PBC)最早应用于机器人控制,由Omega等人将PBC的概念引入到电机控制中。各类电机,无非都是基于法拉第电磁感应定律进行机电能量变换,PBC强调从能量的观点,考虑将电机处理成非线性控制对象,通过配置系统能量耗散特性方程中的无功分量,迫使系统总能量跟踪期望的能量函数,并使系统的状态变量渐近收敛至设定值。电机动态方程中的无功分量则不必抵消,其对系统能量平衡及稳定性无影响,控制器简单、鲁棒性好。文献[17]研究了双馈电机PBC的设计步骤,转速外环与电流内环相互协调,保证了定转子电流及转速的渐近跟踪。针对变速恒频双馈异步风力发电系统,文献[18]提出了一种既能渐近跟踪期望的定转子电流和转速,又可保持定子侧单位功率因数运行的无源控制器,实现了风电系统的最大风能捕获。文献[19]设计了本质上是非线性反馈的PBC,实现了双馈风力发电系统在负载转矩时变未知情形下磁链、转速的渐近跟踪控制。文献[20]论证了BDFM的无源性,给出了d-q轴旋转坐标下的转速控制器。
根据无源性控制理论,本文将BDFM的转子磁链参考值作为转矩控制器的输入,并在转矩控制器前加上线性调节器,通过渐近跟踪磁链设定值,调节BDFM的转速和转矩。控制器中加入了非线性阻尼,系统收敛快速。
1BDFM的无源性分析
1.1BDFM的数学模型
BDFM定子的功率绕组直接接工频电源,控制绕组通过变频器与工频电源连接。
功率绕组子系统在其同步旋转坐标系下的d-q轴电压和磁链方程为[21]
(1)
(2)
控制绕组子系统在其同步旋转坐标系下的d-q轴电压和磁链方程为
(3)
(4)
式中:uqp、udp、iqp、idp、ψqp、ψdp、rp、Lp、Lmpr、ψqrp、ψdrp——功率绕组的电压、电流、磁链、电阻、自感、功率绕组与转子之间的互感和功率绕组转子磁链的q轴和d轴分量;
uqc、udc、iqc、idc、ψqc、ψdc、rc、Lc、Lmcr、ψqrc、ψdrc——控制绕组的电压、电流、磁链、电阻、自感、控制绕组与转子之间的互感和控制绕组中转子磁链的q轴和d轴分量;
ωr、ωp、ωc、ωsp、ωsc——机械角速度、功率绕组和控制绕组的角频率和转差角速度;
D——微分算子;
上标p、c——功率绕组同步速坐标系、控制绕组同步速坐标系;
下标p、c、s、r——功率绕组、控制绕组、定子侧、转子侧的物理量;
下标d、q——d-q坐标系下q、d轴分量。
BDFM的电磁转矩方程为
Te=Tep+Tec
(5)
其中:
(6)
式中:Tep、Tec——功率绕组子系统和控制绕组子系统产生的电磁转矩。
运动方程为
(7)
式中:J、Kd、Tl——转子的转动惯量、阻尼系数和负载转矩。
1.2BDFM控制绕组的Euler-Lagrange系统
BDFM功率绕组与电网直接相连接,其电压的大小和频率由电网决定,通过调节BDFM控制绕组的电压和频率,就可以控制电机的运行模式。为分析BDFM的无源性,现将式(3)转化为EL方程的形式,电流的状态方程为
(8)
其中:
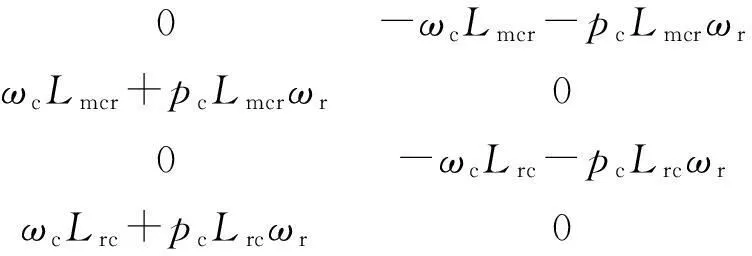
式中:u和i——控制绕组子系统的输入电压矢量和输出电流矢量;
M和R——分别为控制绕组子系统的电感矩阵和电阻矩阵;
W——与控制绕组子系统有关的项;
C和CT——反对称矩阵。
1.3BDFM控制绕组无源性分析
分别对BDFM控制绕组的电气子系统和机械子系统进行无源性分析。
忽略绕组的电容效应,定义BDFM控制绕组中电气部分的能量函数为
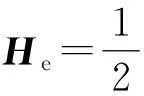
(9)
对时间求导:
(10)
将式(8)代入式(10):
(11)
因C具有反对称性,即iTCi=0,所以Ci项不会影响系统的能量变化,也就不会影响系统的稳定性。因此,在设计BDFM控制策略时,可忽略该部分的非线性因素,可以认为是一个配置系统无功分量的过程。
将式(11)两边进行积分可得
He(t)-He(0)=∫0tiTudτ-∫0tiTRidτ-
∫0tiTWddτ<∫0tiTudτ
(12)
式(12)左边是控制绕组电气子系统能量的增量,右边为电机从电源获取的能量。现将u视为电气子系统输入,则iT为子系统输出。右边第二项实际就是电气子系统内部的电阻消耗、第三项则为电气子系统中转化为机械能部分的能量。式(12)表明,控制绕组电气子系统磁场储存能量的增加量,总是小于控制绕组从电源获得的能量,所以电气子系统是严格无源的。
假设BDFM转轴为刚性,即BDFM机械部分存储的能量全部为动能,则其能量函数可定义为
(13)
对式(13)进行时间求导后代入式(7),积分后可得
(14)
式(14)左边为机械子系统所增加的能量,右边为机械子系统输入的能量。若将Te-TL视为机械子系统输入,ωm视为机械子系统输出,则BDFM的机械子系统严格无源。
由并联系统的无源性原理可知,因为电气子系统和机械子系统均为严格无源的,故其并联形成的整个BDFM系统也是严格无源的。功率绕组、控制绕组和机械三部分子系统的相互连接关系如图1所示。
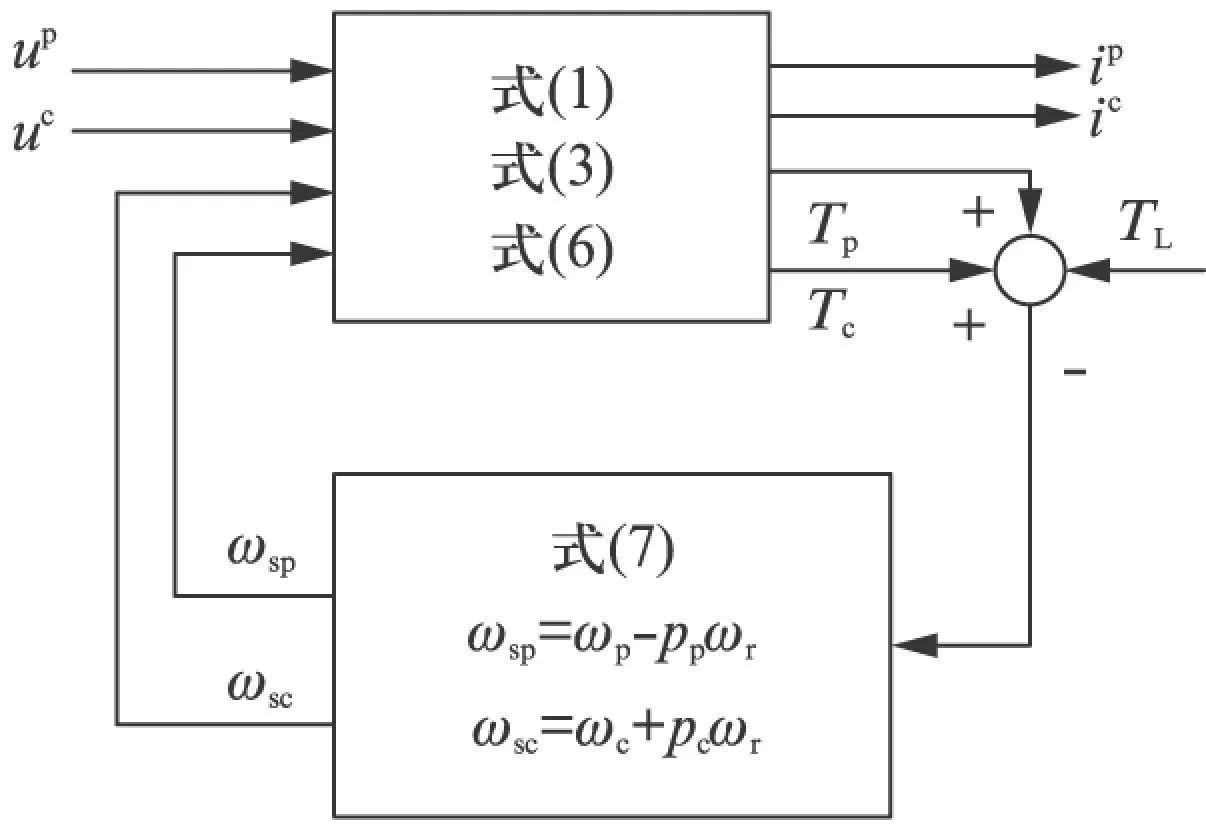
图1 BDFM的反馈互联结构
设计PBC方案时,可将控制绕组电气子系统的能量存储函数作为总的能量函数,机械子系统则可看作是电气子系统的无源干扰。
2基于无源性的控制器设计
2.1转矩控制器设计
为实现转子磁场渐近矢量控制和电磁转矩渐近跟踪,制定如下控制目标:
(1) 电磁转矩渐近跟踪,即
(15)
(2) 控制绕组子系统转子磁链q轴分量渐近定向,即
(16)
(3) 控制绕组子系统转子磁链d轴分量渐近跟踪,即
(17)
为此,定义实际状态与状态期望值之间的跟踪误差为
(18)
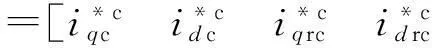
由方程(8),可得到系统的误差方程:
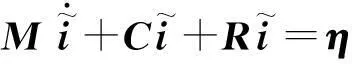
(19)
式中:η——作用于系统的扰动。
(20)
定义误差方程的能量存储函数为
(21)
求式(21)对时间的导数,有:
(22)
由于C为反对称矩阵,所以式(22)右边第一项为零,整理上式,可得
(23)

功率绕组与电网直接连接,计算功率绕组磁链时,可忽略其电阻压降。即功率绕组磁链为
(24)
将功率绕组子系统的磁链与其对应的同步速旋转坐标系的d轴重合,得到以下关系,即:
(25)
整理可得
(26)
在确定转速下,功率绕组同步速坐标系中转子电流分量将为恒定值。
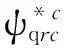
(27)
由式(3)的第3行可得到控制绕组的转差角速度为
(28)
令η=0,由式(3)的1、2行可得PBC系统的控制律为
(29)
将式(27)、式(28)代入式(29),化简可得
(30)
为保证整个控制系统严格无源,改善系统动态响应并降低控制系统对参数变化的灵敏度,对控制量式(30)注入阻尼项,可得
(31)
式中:k——阻尼系数。
恒定阻尼注入,虽可改善系统动态响应,但会影响系统稳态性能,因此提出变阻尼控制策略。变阻尼通过跟踪微分器实现,在电机起动或动态过程开始时采用大阻尼,随后实行自动调节,从而改善动态响应。
针对BDFM的控制系统,所采用二阶微分跟踪器实现变阻尼的注入。若二阶跟踪微分器输入一个信号v(t),它将输出两个信号x1和x2,其中x1跟踪输入信号v(t),x2作为v(t)的“近似微分”。其形式为
(33)
其中:
(34)
同理,在BDFM控制系统中注入变阻尼时,可在电机起动时注入较大阻尼,接近稳态时切换至较小阻尼。因此,将跟踪微分器的输出倒用,获得变阻尼注入的形式为
(35)
其中:
(36)
式中:k1——起动时希望注入的阻尼值;
k2——接近稳态时希望注入的较小阻尼值;
k——阻尼输出值。
2.2转速控制器设计
基于无源性的BDFM转矩控制系统,能够渐近跟踪时变的转矩,只要建立转速误差反馈,采用比例积分调节器,就能够得到下述参考转矩方程:
(37)
式中:kp、ki——比例、积分增益。
可构建BDFM无源控制系统,如图2所示。
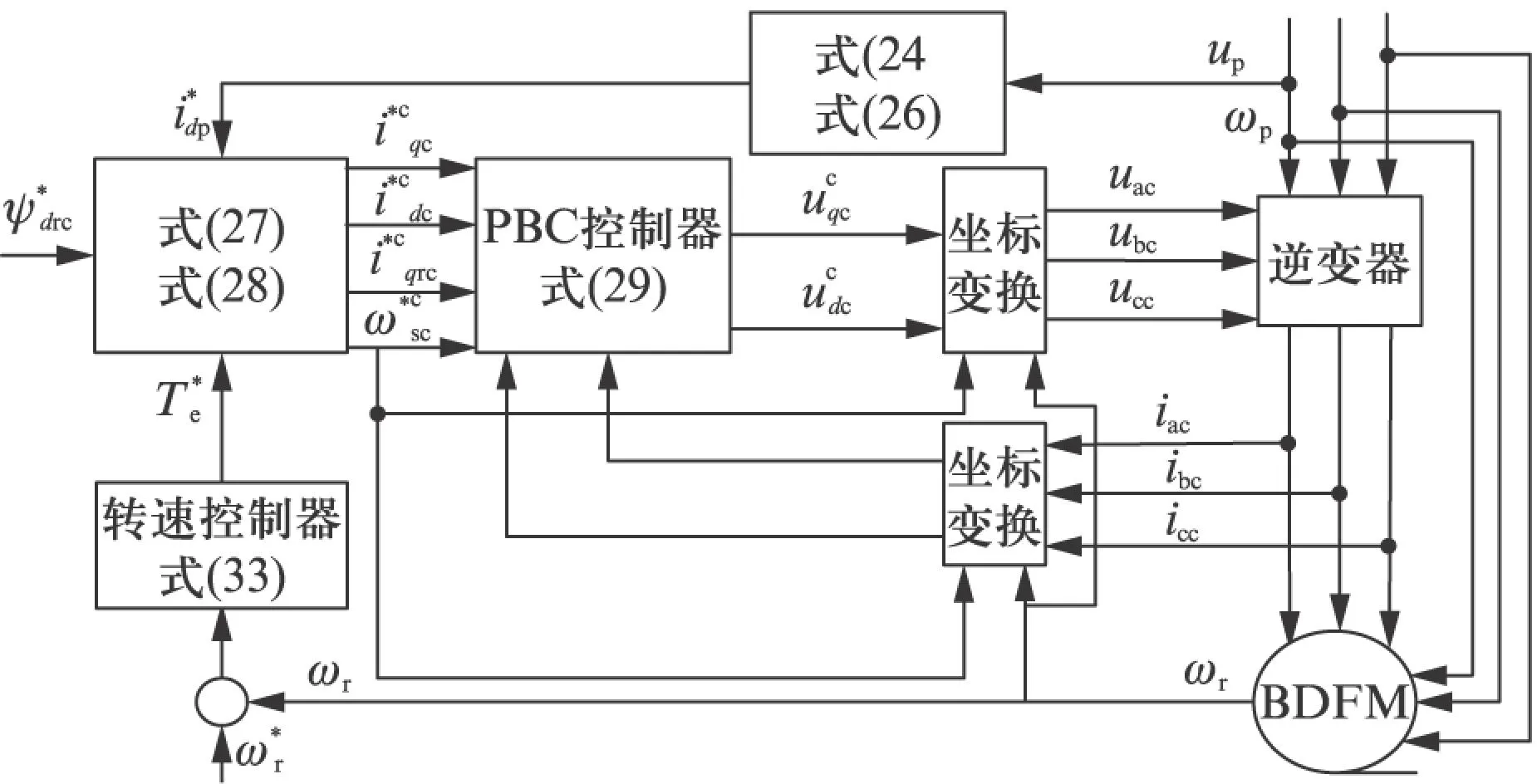
图2 BDFM的无源控制结构
3系统仿真试验
在MATLAB/Simulink平台上搭建系统的各个模块,建立系统的仿真模型并进行仿真。系统参数如下:pp=3,pc=1,rp=0.43Ω,rc=0.436Ω,rr=1.63Ω,rrp=rrc=0.5Rr=0.815Ω,Lp=71.38mH,Lmpr=69.31mH,Lc=65.33mH,Lmcr=60.21mH,Lr=142.8mH,a=70,J=0.03kg·m2,kp=10,ki=0.03,δ=0.003。
图3为BDFM的初始转速给定为750r/min时,空载起动,系统在0.25s时达到稳定,在2.5s时加入负载10N·m突变系统的动态响应波形。负载变化时,系统转速超调量超过设定值的20%,并伴随小幅振荡,输出转矩跟踪迅速,在2.8s时系统重新达到稳定,整个过程中,转速波动较小,无超调现象。

图3 负载变化时动态响应
图4为BDFM初始转速给定为600r/min时,转速出现超调现象,系统经过0.3s的小幅振荡后达到稳定,在2.5s时转速给定突增到900r/min的动态响应波形。由图4可见,转速动态响应迅速,最大超调量不超过设定值的10%,在2.8s时系统达到电磁转矩平稳。

图4 转速变化时动态响应
4结语
在笼型转子BDFM的转速控制中引入无源性非线性控制方法,从能量的角度分离出系统“无功力”,有效简化控制器设计,提高了系统鲁棒性。以变结构的形式注入非线性阻尼,提高了系统收敛速度,改善系统动态响应。仿真结果验证了方法的可行性。
【参考文献】
[1]LI R,WALLACE A, SPEE R.Dynamic simulation of brushless doubly-fed machines[J]. IEEE Transactions on Energy Conversion, 1991,6(3): 445-452.
[2]ZHOU D, SPEE R,ALEXANDER G C, et al. Experimental evaluation of a rotor flux oriented control algorithm for brushless doubly-fed machines[J]. Power Electronics, IEEE Transactions on Power Electronics, 1997,12(1): 72-78.
[3]POZA J,OYARBIDE E, ROYE D.New vector control algorithm for brushless doubly-fed machines[C]∥Proceedings of the 28th IEEE Conference on Industrial Electrons Society Conference, Scvillc, Spain, 2002: 1138-1143.
[4]黄守道,王耀南,黄科元.无刷双馈电机转子磁场定向控制策略的研究[J].电工技术学报,2002, 17(2): 34-39.
[5]刘晓鹏,张爱玲,樊双英.无刷双馈电机直接转矩控制策略的研究[J].微特电机,2006,34(3): 25-31.
[6]BRASSFILED W R, SPEE R, HABETLER T G.Direct torque control for doubly-fed machine[J].IEEE Transactions on Industry Applications, 1996,32(5): 1098-1104.
[7]张爱玲,张洋.基于转矩预测控制的无刷双馈电机直接转矩控制系统[J].电机与控制学报,2007, 11(4): 326-330.
[8]SARASOLA I, POZA J, RODRIGUEZ M A, et al. Predictive direct torque control for brushless doubly fed machine with reduced torque ripple at constant switching frequency[C]∥The 2007 IEEE International Symposium on Indusfirial Elecfironics, Vigo, USA: IEEE, 2007: 1074-1079.
[9]JOVANOVIC M G, G DORRELL D. Sensorless control of brushless doubly-fed reluctance machines using an angular velocity observer[C] ∥The 7th International Conference on Power Electronics and DriveSystems, Piscataway, NJ: IEEE, 2007: 717-724.
[10]周欣欣,张爱玲.无刷双馈电机直接转矩控制转矩脉动最小化[J].电机与控制学报,2006,10(6): 571-575.
[11]蔡晓名,杨向宇.基于模糊PID的无刷双馈电机矢量控制[J].微特电机,2005,33(11): 30-32.
[12]郭红霞,杨金明,刘文刚.无刷双馈电机的PID神经网络控制[J].控制理论与应用,2008,25(1): 53-56.
[13]杨俊华,吕惠子,吴捷,等.基于波波夫超稳定性的无刷双馈电机直接转矩控制[J].中国电机工程学报,2009,29(15): 107-113.
[14]ZHOU D, SPEE R, WALLACE A K.Model refer-ence adaptive speed control for doubly fed machines[C]∥Proceedings of the 19th Annual Conference of IEEE Indusfirial Elecfironics, New York, IEEE, 1993,2(2): 1175-1180.
[15]杨俊华,李建华,吴捷,等.无刷双馈风力发电机组的模糊自适应控制[J].电机与控制学报,2006,10(4): 346-350.
[16]刘航航,韩力.无刷双馈电机控制策略发展综述[J].微特电机,2010(6): 69-73.
[17]高勇,张文娟,杨媛,等.基于无源性的变速恒频双馈风力发电机控制系统[J].电工技术学报,2010,25(7): 130-136.
[18]高勇,张文娟,杨媛,等.变速恒频双馈异步电机无源性控制[J].太阳能学报,2010,31(11): 1491-1496.
[19]钱平,葛翔.双馈感应风力发电机的无源性控制方法研究[J].太阳能学报,2009,30(11)1540-1545.
[20]吕惠子,杨俊华,吴捷,等.无刷双馈调速电机无源性分析及自适应控制[J].控制理论与应用,2009,26(12): 1425-1429.
[21]邓先明.无刷双馈电机的电磁分析与设计应用[M].北京: 机械工业出版社,2008.
[22]NICKLASSON P J, ORTEGA R, ESPINOS G P. Passivity-based control of a class of Blondel-Park transformable electric machines[J]. IEEE Transac-tions on Automatic Control, 1997,42(5): 629-647.
[期刊荣誉]
中文核心期刊中国科技核心期刊中国学术期刊(光盘版)
全国优秀科技期刊华东优秀科技期刊
中国科学引文数据库来源期刊中国学术期刊综合评价数据库来源期刊
