考虑信号幅值和正交误差的旋转变压器解码算法
2016-01-06李伟伟,王爽,程天威等
考虑信号幅值和正交误差的旋转变压器解码算法
李伟伟1,王爽1,程天威1,李光耀2
(1. 上海大学 机电工程与自动化学院,上海200072;
2. 上海电机系统节能工程技术研究中心有限公司,上海200063)
摘要:在传统同步参考坐标系锁相环(SRF-PLL)解码算法的基础上介绍了一种双同步参考坐标系锁相环(DSRF-PLL)解码算法。由于旋转变压器在实际应用中受本体设计及信号处理电路的影响,其输出往往为包含误差的非理想信号,其中幅值不平衡和相位非正交误差占主要地位。DSRF-PLL算法将非理想信号分解成一个正序电压分量和一个负序电压分量,通过双同步坐标系(DSRF)和解耦网络结构单元来达到消除幅值不平衡和相位非正交两种误差的目的。在MATLAB/Simulink环境下搭建仿真模型对DSRF-PLL解码算法进行了仿真验证。仿真结果表明该算法在抑制旋转变压器输出幅值平衡和相位非正交误差方面的有效性。
关键词:旋转变压器; 双同步参考坐标系; 锁相环
基金项目:* 上海张江国家自主创新示范区专项发展资金重点项目(201310-PT-B2-008)
通讯作者:王爽
中图分类号:TM 301文献标志码: A
收稿日期:2015-06-19
A Decoding Algorithm for Resolvers with Amplitude and Quadrature Errors
LIWeiwei1,WANGShuang1,CHENGTianwei1,LIGuangyao2
(1. School of Mechatronic Engineering and Automation, Shanghai University, Shanghai 200072, China;
2. Shanghai Engineering Research Center of Motor System Energy Saving Co., Ltd., Shanghai 200063, China)
Abstract:A double synchronous reference frame-based phase-locked loop (DSRF-PLL) decoding algorithm was studied in this thesis based on the traditional synchronous reference frame-based phase-locked loop (SRF-PLL) decoding method. In practical application the output signals of the resolvers were always non-ideal for the influence of the design of the motor structure and the peripheral circuits, among them amplitude error and non-orthogonal error dominate. In DSRF-PLL the non-ideal signals were decomposed by a positive sequence voltage and a negative sequence voltage; The amplitude error and the non-orthogonal error were eliminated by the double synchronous reference frame (DSRF) and the decoupling network unit. The DSRF-PLL decoding algorithm was verified by simulation in the MATLAB/Simulink, and the simulation results showed that the algorithm could achieve expected effect to deal with the amplitude and the orthogonal errors.
Key words: resolver; double synchronous reference frame; phase locked loop
0引言
在高精度现代交流伺服传动系统中,电机转子位置信息的获取是其中一个关键技术。近年来,无位置传感器的控制得到了广泛研究,但其不适合电机需要频繁起动和低速运行的场合。在众多位置传感器中,旋转变压器具有结构可靠、抗干扰能力强、适用于环境恶劣的场合等优点[1],广泛应用在航空器、卫星天线和机器人中。
旋转变压器的输出信号中包含转子位置信息,经过轴角数字变换器(Resolver Digital Converter, RDC)可以将转子位置信息从旋转变压器输出的模拟信号中提取出来。在实际应用中,旋转变压器由于受结构设计和外围电路的影响,其输出的模拟信号往往是包含误差的非理想信号,主要包括: 幅值不平衡误差、相位非正交误差、谐波误差、直流分量误差等。针对提高旋转变压器测量精度的问题,国内外学者开展了深入的研究。Hanselman[2]详细分析了跟踪型轴角-数字转换的误差来源,例如旋转变压器正余弦信号的幅值不相等、两相信号不正交或含高次谐波时,对测角结果产生的影响。他在文献[3]中提出将旋转变压器两相信号的正交误差转换成幅值误差,进而通过调节两路输出信号幅值放大倍数实现幅值误差的校正。Younjong在文献[4]中提出采用全阶观测器来分离信号中的基波与高次谐波,从而减小谐波信号给解算结果带来的误差,仿真及试验结果证实该算法具有良好的动态特性和鲁棒性。
本文针对旋转变压器幅值不平衡和相位非正交两种主要的输出误差,在传统同步参考坐标系锁相环解码算法(Synchronous Reference Frame Based Phase Locked Loop, SRF-PLL)的基础上研究了一种双同步参考坐标系锁相环解码算法(Double Synchronous Reference Frame Based Phase Locked Loop, DSRF-PLL)。该算法将非理想信号分解成正序电压分量和负序电压分量,通过双同步坐标变换和解耦网络结构单元来达到消除幅值不平衡和相位非正交的目的,从而利用基于锁相环(Phase Locked Loop, PLL)结构的解算单元将位置角信号以及角速度信号准确的解算出来。MATLAB仿真结果验证了该算法的有效性。
1旋转变压器的工作原理
旋转变压器是通过电磁感应原理检测角位置的信号元件,其工作原理如图1所示,由相互独立的转子、定子及绕组构成。在工作时,激磁绕组通以1~20kHz的正弦或余弦激磁信号,通过转子的特殊设计(绕线或变磁阻),使得正、余弦绕组产生与转子位置相关的调制信号。
设激磁绕组的激磁电压uexc为
uexc=Umsin(ωet)
(1)
式中:Um——激磁电压的幅值;
ωe——激磁电压的角频率。
当转子转过θm电角度时,余弦、正弦绕组输出的调制信号ucos、usin分别为
(2)
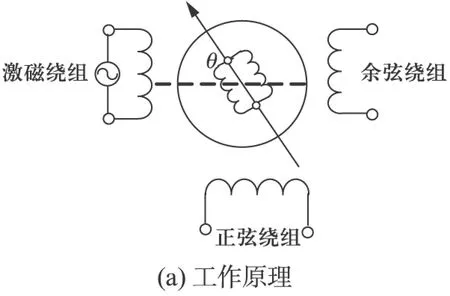
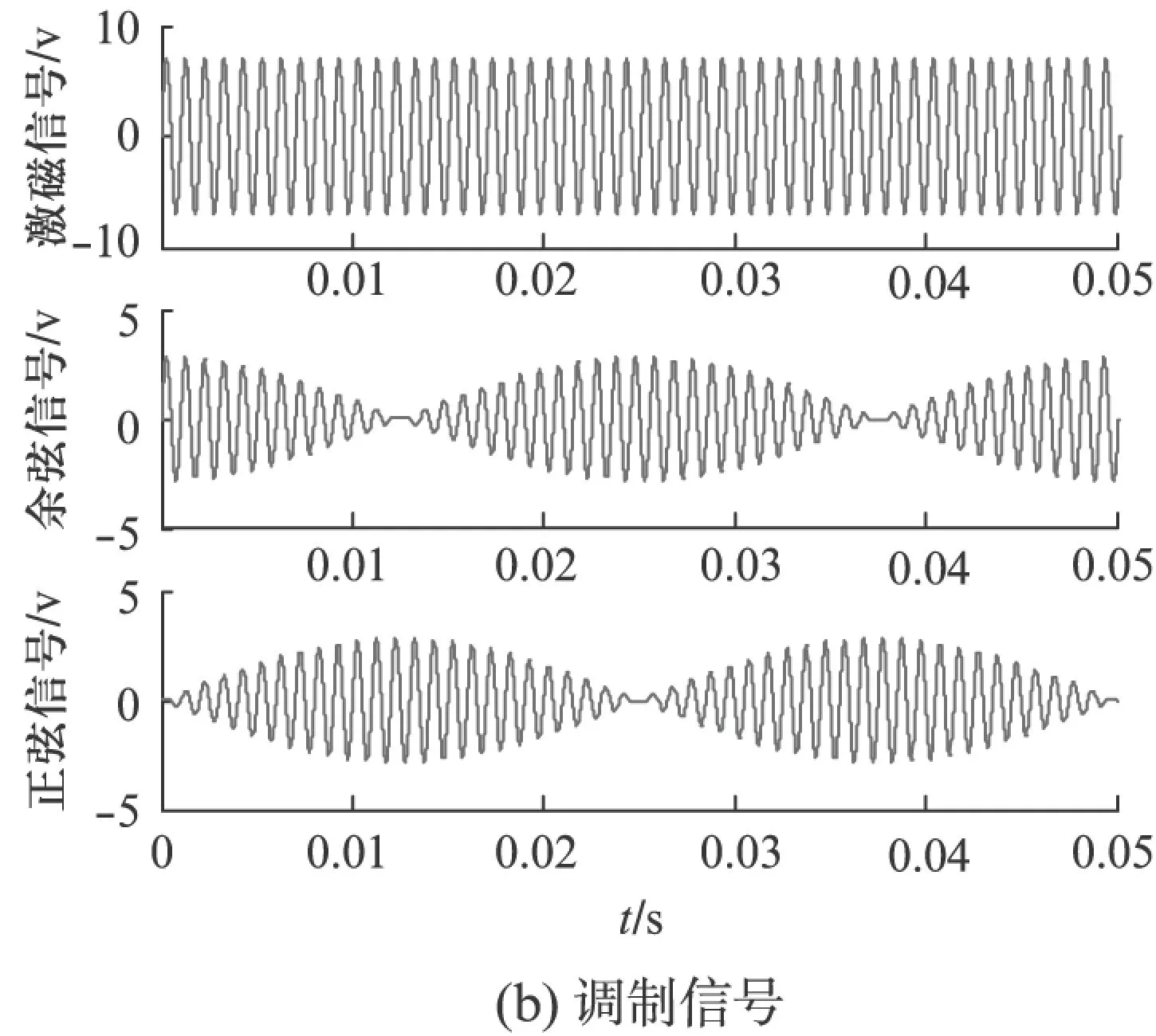
图1 旋转变压器的工作原理
式中:k——旋转变压器的变比;
θm——转子位置角。
2基于SRF-PLL的轴角变换算法
通过式(2)可知旋转变压器输出的正、余弦信号频率与激磁电压信号的频率相同,幅值受到角度为θm的正、余弦函数的调制。ucos、usin的组合唯一确定了位置角θm。基于SRF-PLL算法的旋转变压器轴角变换算法原理如图2所示。该算法主要包括旋转变压器信号的解调和转子位置角的解算。
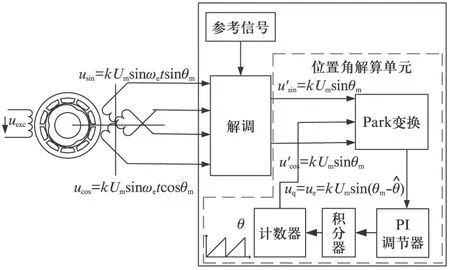
图2 基于SRF-PLL的轴角变换算法原理框图
2.1旋转变压器输出信号的解调
旋转变压器输出信号的解调是将旋转变压器输出的正、余弦包络信号中的激磁信号去除,将其化为标准正、余弦信号;旋转变压器的解调主要有两种方法: 基于欠采样技术的解调方法和过采样技术与频移技术相结合的解调方法。
基于欠采样技术的解调方法存在诸多问题,例如:
(1) 该种方法是在旋转变压器输出信号的每个峰值进行采样,即在激磁信号的每个周期内采样两次,这种采样方法不能充分满足香农采样定理,信号很容易发生混叠;
(2) 如果旋转变压器输出信号存在延迟,那么就不能保证采样时刻和信号峰值同步;
(3) 位置角的解算仅仅依靠信号峰值的采样值,因此会降低位置角的解算精度。
为了克服欠采样解调技术的缺陷,文献[5]提出过采样技术与频移技术相结合的解调方式。
首先利用A/D转换器以高于奈奎斯特频率的采样频率对旋转变压器输出的模拟信号进行采样,这里以ucos和usin来表示。
然后采样后的信号乘以一个与激磁信号同频的信号2sin(ωet)得
(3)
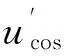
(4)
2.2旋转变压器转子位置角的解算
将解调后正、余弦信号通过正、余弦乘法器后,分别与转子位置角估算信号θ的余弦cosθ、正弦sinθ相乘并做差,其结果与Park变换中uq相同,如式(5)所示:
uq=ue=kUm[sinθmcosθ-cosθmsinθ]=
kUmsin(θm-θ)
(5)
经过反馈闭环,ue值最终趋近于零,可以近似认为θm-θ趋近零,最后通过积分和角度翻转,所得到0~2π间变化信号即为位置角估计信号θ。
3基于DSRF-PLL的轴角变换算法
在实际应用中,受旋转变压器本体及外围电路的影响,其输出的模拟信号通常为包含误差的非理想信号,其中幅值不平衡和相位非正交是两种最主要的误差。
假设以上两种误差同时存在,不失一般性将两种误差都集中到正弦输出信号上,则解调后的旋转变压器输出信号可以用一个矢量us表示为
(6)
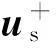
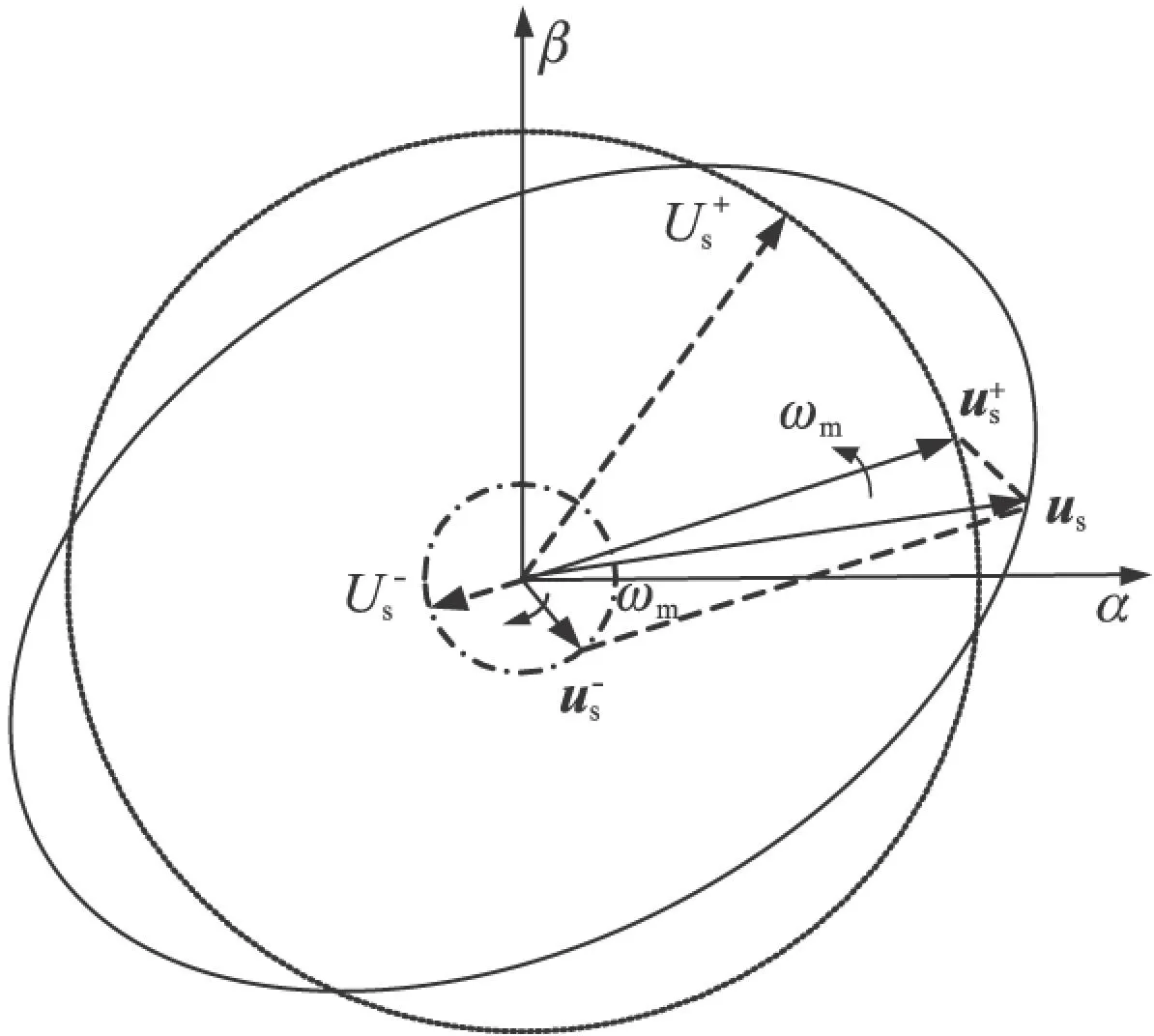
图3 电压矢量轨迹图
(7)
式中: α——幅值误差系数;
β——角度偏差。
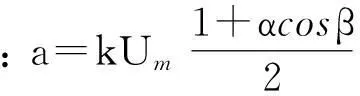
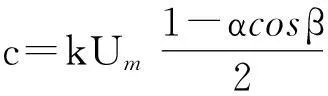
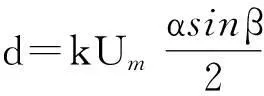
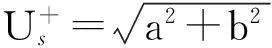
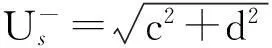
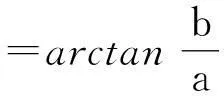
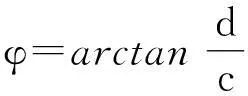
将旋转变压器输出的非理想信号输入到SRF-PLL中进行处理,其解算的位置角θ和角速度ω如图4所示。从图4中可以看出,基于SRF-PLL的解码方法解算出的转子位置角与实际位置角之间存在-0.37~0.06rad的偏差;角速度也存在-70~+45rad/s的波动。
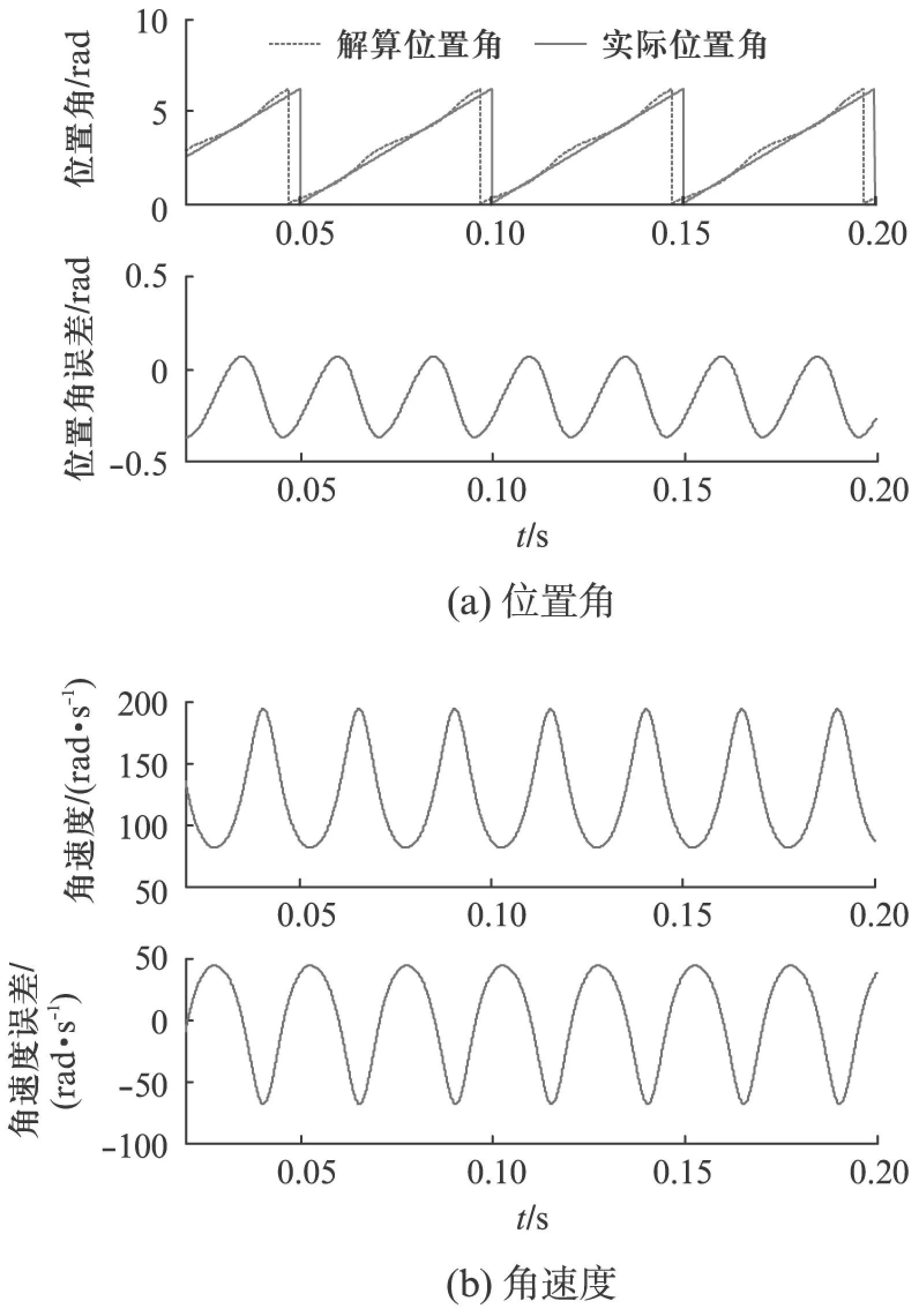
图4 基于SRF-PLL的位置角和角速度解算
DSRF-PLL解码算法的工作原理与SRF-PLL类似。该算法主要包括三部分: 基于DSRF坐标系的旋转坐标变换、解耦网络结构单元和PLL位置角解算单元,其原理如图5所示。

图5 DSRF-PLL结构框图
3.1基于DSRF坐标系的旋转坐标变换
DSRF与传统的SRF类似,由两个坐标系组成:dq+,以角速度ωm逆时针旋转,与α轴线的夹角为θ;dq-,以角速度ωm顺时针旋转,与α轴线的夹角为-θ,如图6所示。
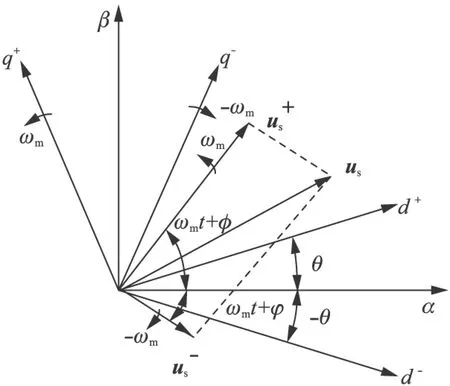
图6 电压矢量和DSRF坐标系
将us在DSRF坐标系下分别进行正向Park变换和反向Park变换有
(8)
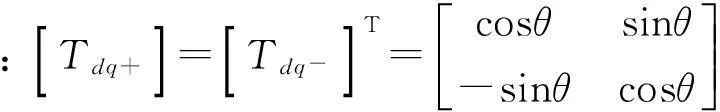
利用一个PLL结构跟踪环并且适当调整控制器的参数可以实现θ≈(ωmt+φ)。此时式(8)可以改写为
(9)
3.2解耦网络结构单元
从式(9)可以看出其算式中包含一个常数项和一个角频率为2ωm的振荡项。该振荡分量是由正向旋转矢量和反向旋转矢量在进行坐标变换时耦合产生的,振荡信号可以看成扰动信号,为了消除扰动信号,设计了一个解耦网络结构单元,如图7所示,其中LPF为一阶低通滤波器低通滤波器,其表达式如式(10)所示:
(10)
设u1=cos2θ、u2=sin2θ,则解耦单元可表达为
(11)
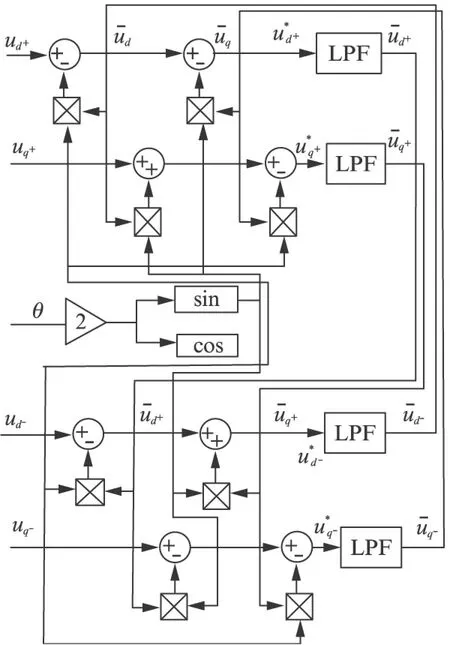
图7 解耦网络结构单元



图8 不同ω f下的正向直轴分量
3.3转子位置角的解算
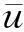
(12)
通过分析可知,这是由于当存在正交误差时,正向旋转矢量的初始位置并不是零,所以当其与真实旋转矢量以相同速度旋转时,会始终存在一个角度偏差,而DSRF-PLL跟踪的是正向旋转矢量,因此得到结果也就是与真实值有一个恒定误差。该恒定误差即为当真实角度θ=0时,正向旋转矢量与α轴的夹角。
4仿真结果
为了验证DSRF-PLL旋转变压器解码算法的有效性,对DSRF-PLL在MATLAB/Simulink环境下建立的仿真模型进行仿真验证,仿真参数如表1所示,仿真结果如图9~图12所示。

表1 仿真参数
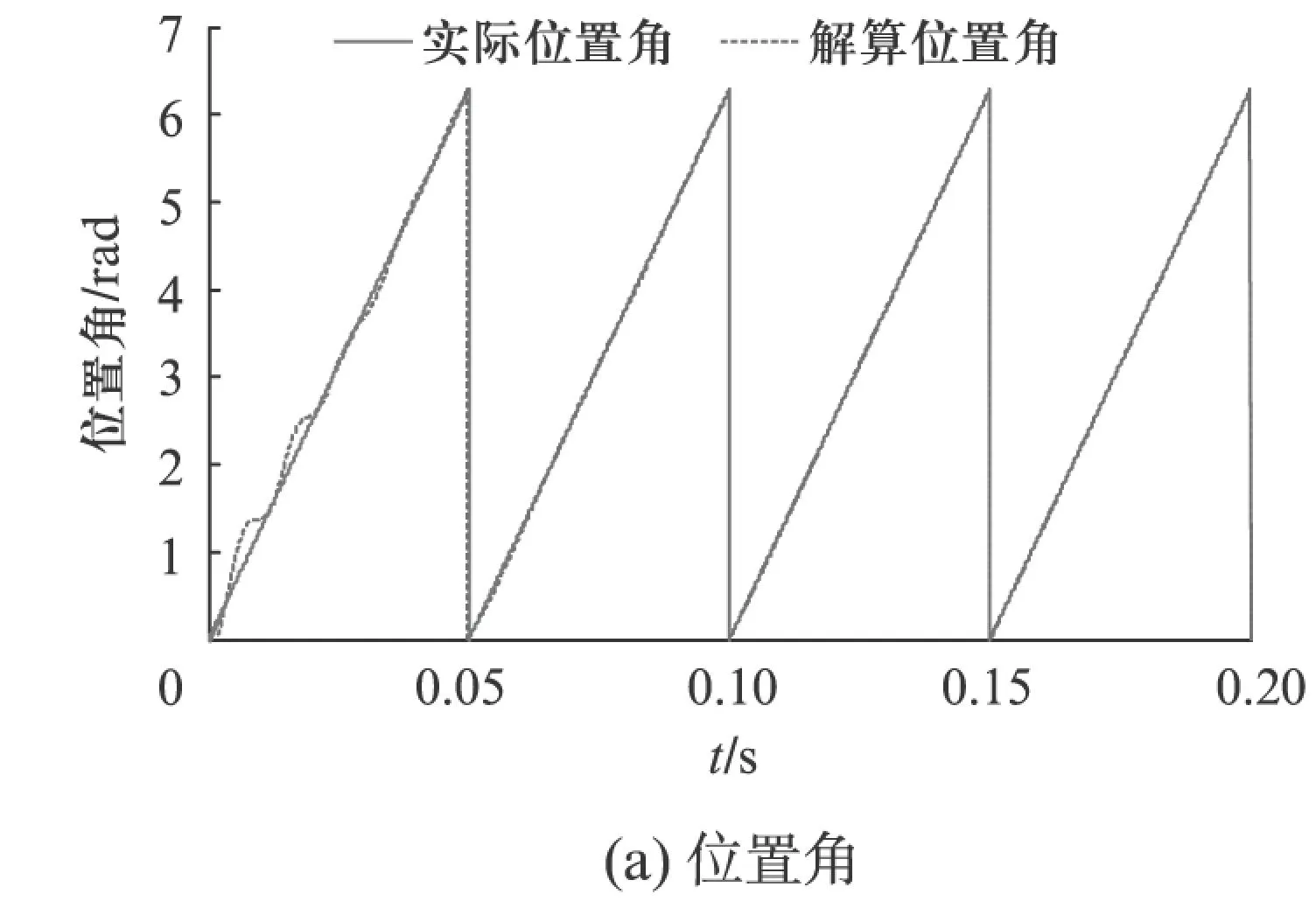
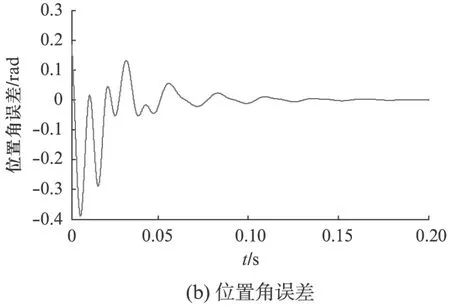
图9 基于DSRF-PLL的解算位置角
图9(a)为基于DSRF-PLL的解算位置角与实际位置角的对比图,由于两种位置角曲线过于接近,不便于分析误差,这里给出实际角位置与解算角位置的差值作为位置误差,如图9(b)所示。从图9(b)中可以看出当解算位置角在极短的时间内锁住实际位置角以后,其位置角的稳态误差为零,即解算位置角亦为实际位置角。图10给出了角速度的解算情况,当系统达到稳定时,角速度稳定在125.66rad/s,没有受到幅值和正交误差的影响,不存在波动。

图10 基于DSRF-PLL的解算角速度

图11 正反向交直轴分量
为了更加直观的表示DSRF-PLL算法在抑制幅值不平衡和相位不正交两种误差方面的有效性,做了如下对比仿真: 在0.2s之前,利用SRF-PLL算法对旋转变压器输出信号进行解码;在0.2s时刻切换到DSRF-PLL算法对旋转变压器输出信号进行解码。从图12中可以很清晰地看出由DSRF-PLL算法解算出的位置角更加精确,其角速度更加平稳。
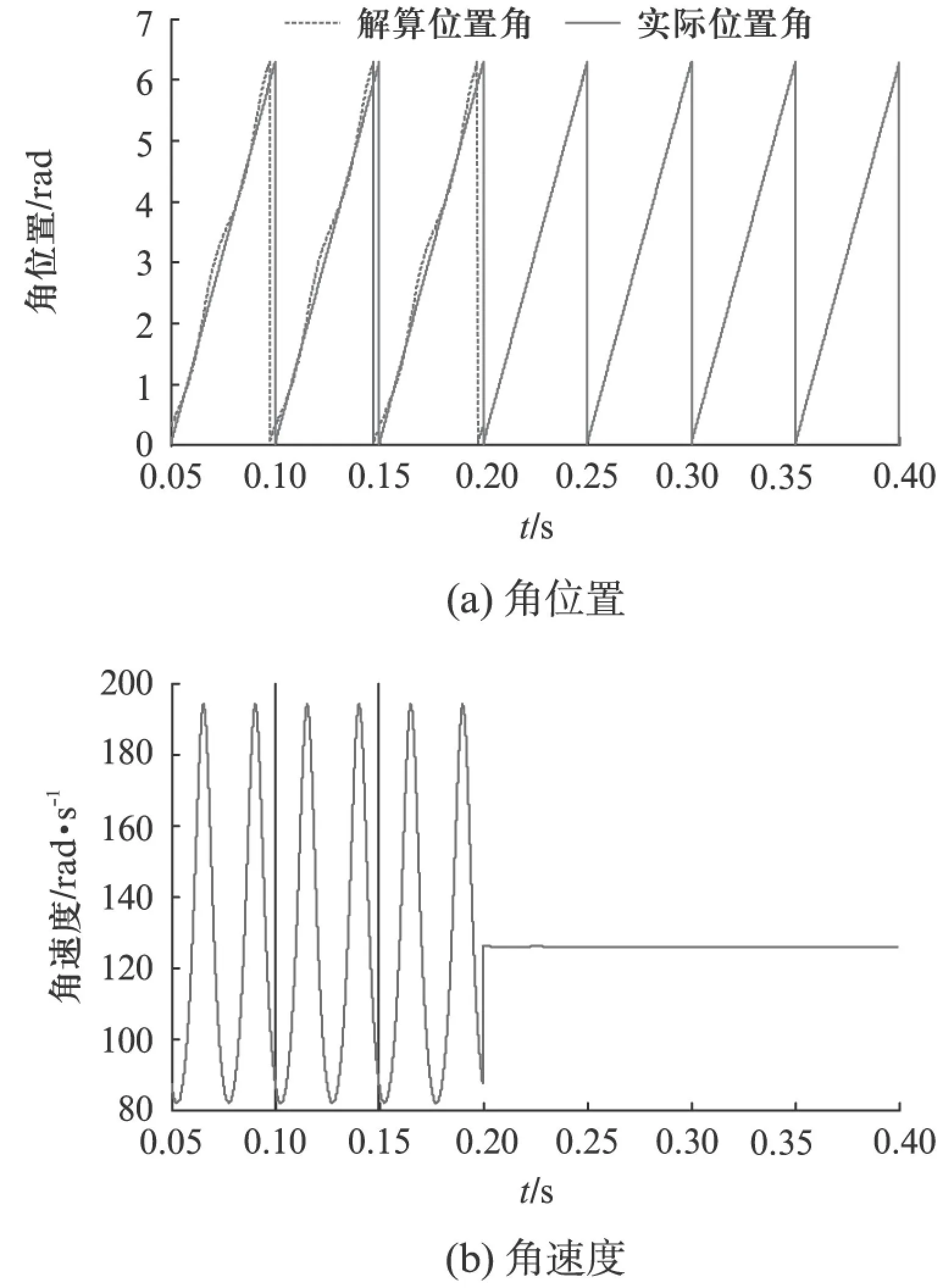
图12 角位置与角速度信号对比图
5结语
传统的SRF-PLL解码算法结构简单、易于执行,具有快速性和实时性的特点,但是当旋转变压器的输出包含幅值不平衡和非正交误差时,其解算效果却并不理想。本文所研究的DSRF-PLL解码算法有效地抑制了旋变输出信号中的幅值和正交误差,其研究对于高精度、低成本的轴角数字转换器的实现提供了技术参考。
【参考文献】
[1]HOSEINNEZHAD R. Position sensing in brake-by-wire callipers using resolvers[J]. Vehicular Technology, IEEE Transactions on, 2006,55(3): 924-932.
[2]HANSELMAN D C. Resolver signal requirements for high accuracy resolver-to-digital conversion[J]. Industrial Electronics, IEEE Transactions on, 1990,37(6): 556-561.
[3]HANSELMAN D C. Techniques for improving resolver-to-digital conversion accuracy[J]. Industrial Electronics, IEEE Transactions on, 1991,38(6): 501-504.
[4]YOUN J, PARK K, LEE K B, et al. A new PLL system using full order observer and PLL system modeling in a single phase grid-connected inverter[C]∥Power Electronics and ECCE Asia (ICPE & ECCE), 2011 IEEE 8th International Conference on, IEEE, 2011: 803-808.
[5]BERGAS J J, FERRATER S C, GROSS G, et al. High-accuracy all-digital resolver-to-digital conversion[J]. Industrial Electronics, IEEE Transactions on, 2012, 59(1): 326-333.