基于有限元与光滑粒子耦合的弹丸挤进过程分析

第一作者马明迪男，硕士,助理工程师，1988年12月生

通信作者曾志银男，教授级高工，1957年4月生

基于有限元与光滑粒子耦合的弹丸挤进过程分析

马明迪，崔万善，曾志银，宁变芳，鲁玉祥

(西北机电工程研究所，陕西咸阳712099)

摘要：基于有限元(FEM)与光滑粒子(SPH)耦合算法，建立弹丸身管耦合系统动力学模型。通过对某大口径火炮弹丸挤进过程进行数值模拟，弥补弹丸挤进过程有限元分析方法无法有效模拟弹带大变形缺陷，成功模拟出弹丸挤进阶段弹带塑性流动过程，在此基础上深入研究弹带的应力应变变化规律。分析弹丸初始装填角、弹炮间隙、弹丸装填不到位等因素对挤进过程中弹丸动力响应影响。结果表明，仿真与实弹射击的弹带变形一致性较好。

关键词：挤进过程；弹带；动力响应；有限元法；光滑粒子法

收稿日期：2014-01-08修改稿收到日期：2014-03-27

中图分类号:TP391.9文献标志码：A

基金项目：国家科技重大专项资助项目(2012ZX04010-011)

Engraving process analysis of projectiles based on coupling of FEM and SPH

MAMing-di,CUIWan-shan,ZENGZhi-yin,NINGBian-fang,LUYu-xiang(Northwest Institute of Mechanical & Electrical Engineering, Xianyang 712099, China)

Abstract:Based on the coupling algorithm of finite element method (FEM) and smoothed particle hydrodynamics (SPH) method, the dynamic model of a projectile-barrel coupled system was established. The numerical simulation of the engraving process of projectiles of a heavy caliber gun was performed, it remedied the deficiencies of FEM, FEM couldn’t simulate the large deformation of a bearing band effectively. The plastic flow of the bearing band was successfully simulated in the engraving process of projectiles. Furthermore, the stress and strain varying laws of the bearing band were intensively studied. The influences of initial loading angle of projectile, gap between barrel and projectile and projectile not filled in position on the dynamic responses of a projectile in the engraving process were analyzed. The results showed that the deformations of the bearing bend obtained with simulation agrees well with those measured in live weapon firings.

Key words:engraving process; bearing band; dynamic responses; finite element method; smoothed particle hydrodynamics method

弹丸挤进过程是非常复杂的动力学问题，涉及材料、几何及接触界面等诸多非线性因素，如弹丸与身管内膛的高速碰撞、弹带大变形等，且整个过程历时极短，难以通过实验准确观察、测量，更无法通过常规理论计算准确描述[1]。

对弹丸挤进过程分析大多采用有限元法(Lagrange、Euler、ALE)。Lagrange方法理论成熟，计算效率及求解精度较高，当涉及大变形问题时会出现严重的网格畸变，致求解困难[2]。Euler及ALE方法虽有所改进，但仍存在较大局限性[3]。光滑粒子法(Smoothed Particle Hydro-dynamics，SPH)为纯Lagrange粒子方法[4]，在计算空间导数时无需用任何网格，可有效避免计算中出现的网格畸变、扭曲等问题，因此较适合计算带大变形的高速碰撞等冲击力学问题。SPH方法在每步都需确定每个计算点影响域中的粒子，搜索算法耗时较多，尤其粒子数较多时矛盾更突出，故计算效率低于Lagrange有限元法[5]。

本文在已有研究基础上，考虑大口径火炮弹丸挤进过程的强冲击及弹带大变形等特点，分析中引入有限元法与光滑粒子法耦合算法。对在挤进过程中发生大变形的弹带用SPH法、对身管及弹体等变形小区域用Lagrange有限元法。既可充分利用SPH方法模拟大变形能力，又能发挥出Lagrange有限元法计算效率高优势，能极大限度提高计算效率及精度，弥补常规弹丸挤进过程有限元分析方法不能有效模拟弹带塑性流动的缺陷。

1光滑粒子法

光滑粒子法为求解偏微分方程的数值方法，属于无网格法一种。该方法先对偏微分方程的求解域离散化，再用近似函数表示任一点的场函数及导数，从而将偏微分方程转化为一系列离散化、只与时间相关的常微分方程，通过显式积分法求解常微分方程，获得问题的数值解。

在SPH方法中，任意场变量f(x)(如压力、密度、温度等)及空间导数f(x)可用两式积分近似获得，即

〈f(x)〉=∫Ωf(x′)ω(x-x′,h)dx′

(1)

〈f(x)〉=∫Ωf(x′)ω(x-x′,h)dx′

(2)

图1　粒子近似示意图 Fig.1 Particle approximation

式中：ω(x-x′,h)为核函数或光滑函数，是位置矢量x及光滑长度h的函数[6]。

将整个解域离散成一系列任意分布的粒子，见图1。物理量计算只在粒子上进行，因此核估计积分表达式可化为粒子求和的离散化形式，即

(3)

〈ω(xi-xj,h)

(4)

式中：mj为粒子j的质量；ρj为粒子j的密度；j=1,2,…,N，N为在粒子i影响域内所有粒子总数。

式(3)、(4)进一步揭示了光滑粒子法的本质，即未知函数及导数可用离散点上函数值通过加权平均获得，权因子即为核函数或核函数的导数。本文模型所用核函数为B样条函数，即

(5)

将式(3)、(4)用于所有偏微分方程中场函数的相关项，则可获得一系列仅与时间相关的离散形式常微分方程，用显式积分法求解，即可获得所有粒子的场变量随时间变化值。

2有限元法与光滑粒子法耦合

SPH法与有限元法的计算过程非常相似，二者区别在于SPH法采用离散节点模拟计算域，而有限元法则用连续单元离散计算域。若将SPH粒子仅一个节点的单元，则SPH方法类似于有限元法。在耦合算法中，不同计算区域在界面上存在相互作用，因此需定义该作用。

本文模型涉及的有限元法与光滑粒子法耦合问题包括：①接触界面问题，即弹带与身管内表面的接触-碰撞。本文将弹带SPH 节点定义为从节点，将身管内表面定义为主表面。所用算法本质上与有限元接触算法中罚函数法类似，即每一时间步检查弹带从节点是否穿透主表面，未穿透不做任何处理，否则在该从节点与被穿透的主表面间引入大小与穿透量及主表面单元刚度成正比的接触力。②固连接触问题，即弹带与弹体初始时刻接触部位的固连接触。本文将弹带SPH粒子定义为从节点，将与SPH 粒子接触界面的弹体单元表面定义为主表面，若弹带从节点与对应的主表面存在微小距离，则采用正交投影方法将从节点移到主表面[7]。

在固连接触中，物理量求解过程为：对非接触表面的SPH粒子及Lagrange 单元，从接触表面上节点的已知速度、位移开始，由Lagrange单元的物理量计算相应单元应力、应变率等，由SPH粒子的物理量计算SPH粒子应力、应变率等；在此基础上确定每个Lagrange单元节点的力、SPH 粒子及粒子周围临近节点所受力；再计算下一时刻所有节点的速度、位移。循环直至完成整个求解时间内计算。

3计算模型

本文以某大口径火炮弹丸身管耦合系统为研究对象，计算模型包括身管及弹体有限元模型及弹带SPH模型。

3.1有限元模型

身管模型除膛线起始处采用棱柱单元外，其余均用六面体单元。该身管为混合膛线，结构复杂。本文利用循环对称性切分结构进行拓扑变换，从膛线起始处划分网格，用分段扫描拉伸方式沿膛线空间曲线扫描，获得身管有限元模型。坡膛处局部图见图2。弹体有限元模型见图3。

图2 坡膛细节图Fig.2Chamberthroatdetails图3 弹体有限元模型Fig.3FEMmodelofprojectilebody

3.2弹带SPH模型建立

为精确控制弹带光滑粒子分布，建立有限元网格，将弹带节点转化为SPH粒子。由于膛线存在一定缠度，弹带被阳线刻出的沟槽也有一定角度，为减小SPH粒子移动，在处理弹带网格时使其保持与膛线初始缠角相同角度。所建弹带有限元模型及转化的SPH模型见图4。

(a) 弹带有限元模型(b) SPH模型图4 弹带有限元模型与SPH模型Fig.4FEMandSPHmodelofbearingband

3.3材料模型

身管为炮钢材料，采用双线性模型。弹带为H96黄铜，采用Johnson-Cook本构模型，可描述材料在大变形、高应变率及高温条件下的力学行为。Johnson-Cook模型流动应力表达式为

(6)

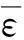
采用Gruneisen状态方程

(γ0+aμ)E

(7)

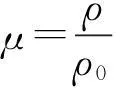
由于挤进过程中重点关注弹带与身管间的作用过程，为提高计算效率，弹体简化为刚体。

4数值模拟及结果分析

模型采用0号装药，据设计提供的弹底压力-时间曲线施加弹底压力，以模拟火药气体对弹丸的冲击作用。取点火时刻为时间原点，弹底压力-时间曲线见图5。

图5　压力-时间曲线 Fig.5 Curves of pressure-time

由于挤进部位距身管约束端很近，且挤进过程历时极短，故不考虑身管与弹丸自重影响。

本文对4种工况进行模拟，即①理想工况： 弹炮间隙为0.02 mm(身管阳线及弹丸前定心部均采用名义尺寸)，弹丸轴线与身管轴线重合；②初始装填角：弹炮间隙为0.02 mm，弹丸初始装填角取0.4′；③弹炮间隙增大：身管阳线半径取公差上限，弹丸前定心部取公差下限，弹炮间隙增大到0.22 mm，弹丸轴线与身管轴线重合；④装填不到位：弹炮间隙为0.02 mm，弹丸与身管轴线重合，弹丸距设计合膛位置50 mm。

4.1弹带变形分析

利用SPH方法模拟的挤进阶段弹带塑性流动过程，见图6。由图6看出，弹丸在坡膛中前进时，随坡膛内径不断减小，后弹带突起部分逐渐被挤压变形产生塑性流动，向后弹带凹槽内填充。约2 ms时前弹带刻槽基本完成，与阳线接触的弹带材料一部分在阳线挤压下沿阳线上表面法线方向压缩，另一部分在阳线剪切作用下向后塑性流动填充到前弹带环形凹槽处及前后弹带中间区域。约3 ms时，弹带完全挤入直膛段，挤进过程结束。

图6　弹带变形过程 Fig.6 Deforming process of bearing band

4.2弹带应力应变分析

工况1弹带在不同时刻等效应力分布见图7。由图7看出，随弹丸逐渐挤进坡膛，弹带外缘突起部分被坡膛挤压出现应力集中；随弹丸继续向前运动，弹带受膛线挤压及剪切作用加大，应力进一步增大直至挤进过程结束，弹带等效应力最大可达550 MPa以上；随弹丸进入直膛段后刻槽完成，弹带承受的向后剪切及径向挤压力明显减小，出现卸载现象，整体应力水平有所下降。

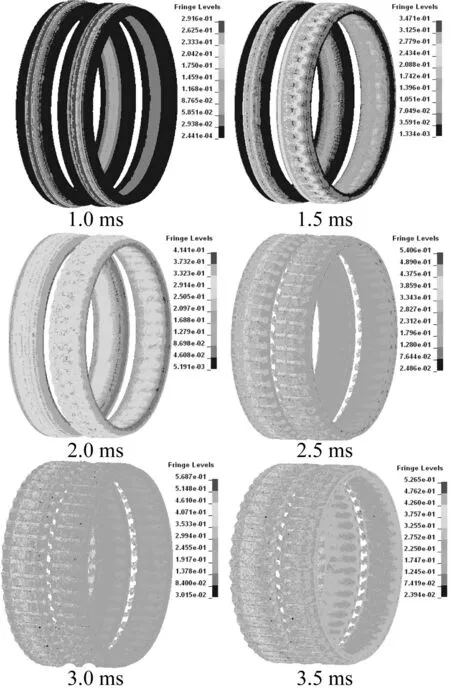
图7　工况1弹带等效应力分布图 Fig.7 Distribution map of equivalent stress of bearing band in operating mode 1

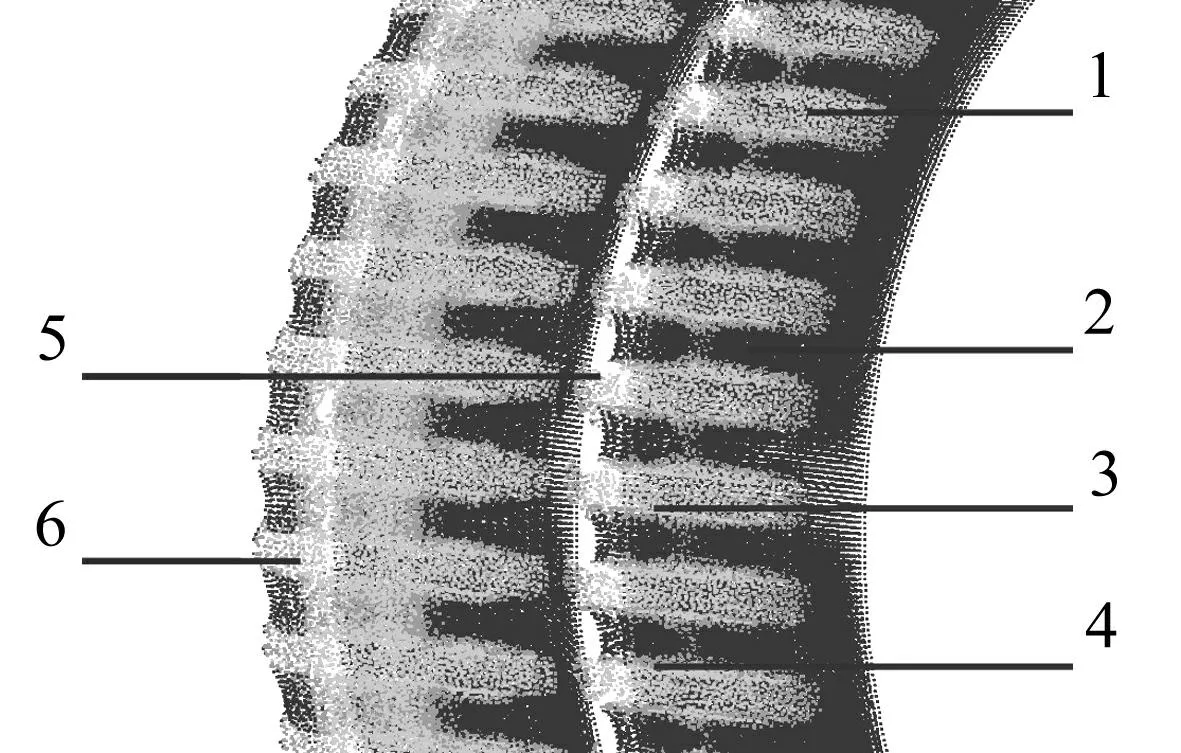
图8　弹带分析选取粒子 Fig.8 Selected particles on bearing band

选取弹带上不同部位的光滑粒子进行响应分析。挤进结束时所选粒子分布见图8。由图8看出，1号粒子位于与阳线上表面相接触的凹槽内；2号粒子位于与阴线表面相接触凸起处；3号粒子位于与阳线导转侧接触部位；4号粒子位于与阳线非倒转侧接触部位；5、6号粒子为挤进过程中受膛线剪切、挤压作用流动到弹带后方的粒子。

弹带上1~6号粒子等效应力随时间变化曲线见图9。由图9看出，随弹丸挤进坡膛，弹带等效应力迅速增大。在挤进过程中，应力波动剧烈，此因挤进过程中受力复杂，出现反复加载-卸载所致。弹带挤进结束后，弹带等效应力逐渐稳定在一定范围内。弹带与阳线接触挤压部分因受径向挤压及摩擦作用较大，应力水平相对较高；弹带塑性流动部分在挤进过程中受膛线剪切、挤压作用，流动到弹带后方预留的区域中，挤进结束后受阳线作用显著减小，卸载现象明显，因此等效应力先增大后减小趋势较明显。

1~6号粒子等效应变随时间变化曲线(1~6号粒子位置见图8)见图10。由图10看出，粒子在挤进过程中塑性应变迅速增加，挤进结束后应变趋于稳定，由于此后身管缠角变化很小，故弹带塑性变形增加趋势不明显。

由于弹带应力应变与膛线对弹带挤压、剪切等作用力直接相关，即由弹带及身管的径向过盈量决定，因此初始装填角及装填位置对弹带应力应变分布影响不大。初始装填角会导致开始一段时间弹带出现受力不对称，但随弹丸在前进中受身管约束而不断归正姿态，弹带应力应变逐渐呈对称分布。弹炮间隙增大，弹带与膛线的过盈量减小，导致膛线对弹带的挤压、剪切等作用力均下降，进而导致弹带应力应变水平下降。

4.3弹丸动力响应分析

各工况挤进过程中弹丸运动阻力变化曲线见图11。由图11看出，随弹丸运动行程增大弹带塑性变形量增大，变形阻力随之增大。挤进过程完成时，弹带运动阻力达到峰值。随弹带进入导向部挤进阻力逐渐下降。弹丸初始装填角对弹丸挤进过程中的运动阻力影响不大，弹丸、身管为名义尺寸时，挤进阻力在1 000 kN左右。弹炮间隙增大及装填不到位均可导致弹丸运动阻力减小。

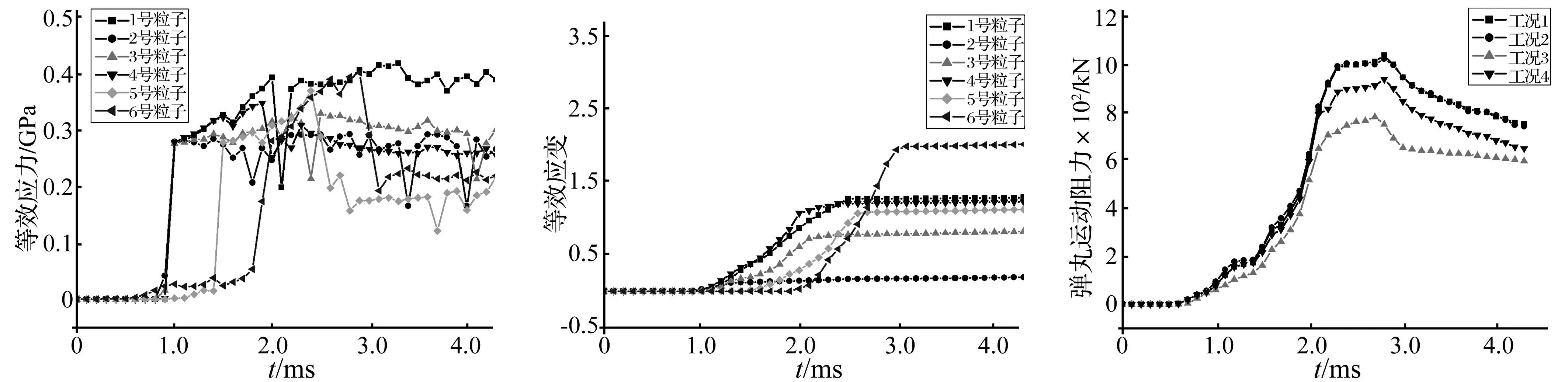
图9 粒子等效应力变化曲线Fig.9Changingcurvesofequivalentstressofselectedparticles图10 粒子等效应变变化曲线Fig.10Changingcurvesofequivalentstrainofselectedparticles图11 各工况下弹丸运动阻力Fig.11Motion-resistanceforceofprojectileineachoperatingmode

各工况下弹丸轴向速度、加速度曲线见图12、图13。由两图看出，初始装填角对弹丸挤进速度、加速度影响不大；弹炮间隙增大及装填不到位将导致弹丸挤进速度、加速度增大。因随弹炮间隙加大弹带与身管内表面过盈量减小，膛线与弹带相互作用减小，弹丸运动阻力减小，弹丸运动速度、加速度增大。由于装填不到位，弹丸在达到卡膛位置前已开始加速运动，导致弹丸运动速度增大。由于挤进进程相对滞后，弹底压力已明显增大，故加速度相对较大。

各工况身管对弹体高低方向撞击力曲线见图14。由图14看出，存在初始装填角时弹丸在加速过程中与身管不断碰撞矫正姿态，撞击频率在1 000 Hz左右；其它工况下挤进阶段碰撞不明显。

图12 各工况弹丸轴向速度对比Fig.12Axialvelocityofprojectileineachoperatingmode图13 各工况弹丸轴向加速度对比Fig.13Axialaccelerationofprojectileineachoperatingmode图14 弹体受高低方向撞击力Fig.14Impactforceonprojectileinhigh-lowdirection

4.4仿真模型验证

仿真与实弹射击对比见图15。由图15看出，弹带刻槽清晰，仿真与实弹射击的弹带变形情况一致性较好。

图15　仿真与实弹射击对比图 Fig.15 Map of comparison between simulation and service firing

5结论

本文针对某大口径火炮弹丸身管耦合系统，综合运用有限元与光滑粒子法，对弹丸挤进过程进行深入研究，结论如下：

(1)利用光滑粒子法在计算大变形的高速碰撞动力学问题上的特有优势，首次在弹丸挤进过程分析中引入有限元法与光滑粒子法耦合方法，成功模拟出弹带被阳线刻槽的塑性流动过程，并在此基础上深入研究弹带的应力应变变化规律，为进一步进行弹丸挤进过程中的弹、炮动力响应机理研究奠定基础。

(2)通过研究弹丸初始装填角、弹炮间隙、弹丸装填不到位等因素对挤进阶段弹丸动力响应影响表明，初始装填角对弹丸挤进阻力、挤进速度、加速度影响不大；弹炮间隙增大及装填不到位均可导致弹丸运动阻力减小，挤进速度、加速度增大。研究结果为身管内膛结构与弹丸匹配设计、进一步深入研究膛线起始段磨损、阳线损伤等问题提供理论依据。

参考文献

[1]孙河洋,马吉胜,李伟,等. 坡膛结构变化对弹带挤进过程影响的研究[J]. 振动与冲击,2011, 30(3): 30-33.

SUN He-yang, MA Ji-sheng, LI Wei, et al. Influence of different bore structures on engraving process on projectile [J]. Journal of vibration and shock,2011, 30(3): 30-33.

[2]许庆新. 基于SPH方法的冲击动力学若干问题研究[D]. 上海: 上海交通大学, 2009.

[3]余丰. 基于SPH_FEM的磨粒加速过程及材料去除机理研究[D]. 济南: 山东大学, 2012.

[4]王吉. 光滑粒子法与有限元的耦合算法及其在冲击动力学中的应用[D]. 合肥:中国科学技术大学, 2006.

[5]肖毅华. 有限元法与光滑粒子法的耦合算法研究[D]. 长沙: 湖南大学, 2012.

[6]张雄,王天舒. 计算动力学[M].北京:清华大学出版社, 2007.

[7]Johnson G R, Stryk R A, Beissel S R. SPH for high velocity impact computations[J]. Computer Methods in Applied Mechanics Engineering,1996, 139: 347-373.