梁桥结构地震反应分析中输入地震动选取及调整方法研究

第一作者张云男，博士，教授级高工，1977年1月生

通信作者谭平男，研究员，博士生导师，1973年9月生

邮箱：ptan@foxmail.com

梁桥结构地震反应分析中输入地震动选取及调整方法研究

张云1,2,3，谭平1，郑建勋1，周福霖1

(1．广州大学减震控制与结构安全国家重点实验室(培育),广州510405；2．广西交通科学研究院,南宁530007；3.广西防灾减灾与结构安全重点实验室,南宁530007)

摘要：针对桥梁结构地震动分析时所输入地震动选择会影响时程分析结果的可靠性，结合结构动力放大系数基本原理及地震波能量原理，通过分析反应谱型特点，将其拟合归纳为以结构自振周期±30%范围及规范规定的0.1s-Tg范围分别定义为低频、高频对比区间，以两个区间反应谱曲线包围面积作为对比参数进行自然地震波选择依据。并据所选地震波提出基于两区间的5种天然地震波调整方法。以典型多跨梁桥为例进行数值分析，以桥墩墩底弯矩、剪力和及墩顶位移作为桥梁地震反应统计量。利用统计分析结果验证双参数地震波选择方法及地震波调整方法的合理性及有效性。

关键词：时程分析；桥梁结构；反应谱谱型；输入地震动

收稿日期：2014-01-08修改稿收到日期：2014-03-19

中图分类号:P315.9文献标志码：A

Selecting and adjusting methods for earthquake input in a girder bridge’s seismic response analysis

ZHANGYun1,2,3,TANPing1,ZHENGJian-xun1,ZHOUFu-lin1(1.State Key Laboratory for Seismic Control and Structural Safety (Cultivation base), Guangzhou University, Guangzhou 510405, China; 2. Guangxi Transportation Research Institute, Nanning 530007, China；3. Guangxi Key Laboratory of Disaster Prevention and Structural Safety, Nanning 530007, China)

Abstract:Time-history analysis method is the most popular seismic analysis one of bridge structures, however, selection of input seismic motion is a key factor to affect the reliability of time-history analysis results. Combining the basic principle of structure dynamic amplification coefficient and the energy principle of seismic wave. The seismic response spectrum of a bridge structure was divided into two intervals, one was a lower-frequency interval with a frequency range of ±30% the structure’s natural vibration period, the other was a higher-frequency one with a frequency range of 0.1 s -Tg regulated by the code. The surrounding areas fo these two intervals’ spectral curves were taken as comparative parameters to choose natural seismic wave records. Five adjusting methods of natural seismic wave records based on the above mentioned two intervals were presented here. In addition, seismic response numerical analysis of a typical multi-span bridge was performed, bridge pier bottom moment, base shear and pier top displacement were taken as statistical values of the bridge’s seismic responses. Numerical analysis results showed that the double-parameter selecting and adjusting methods for seismic wave records are reasonable and effective.

Key words:time-history analysis; bridge structure; spectral shape; inputting earthquake record

《公路桥梁抗震设计细则》(JTG/T B02-01- 2008)将桥梁分为A、B、C、D四个类别。并规定对A、B、C三类桥梁均需进行E1、E2地震作用下抗震设计，计算方法为多振型反应谱法(规则桥梁)及非线性时程分析方法(非规则桥梁)。三类桥梁涵盖我国二级及以上所有公路桥梁。时程分析方法已成为桥梁结构地震响应分析常用方法，所用计算软件如SAP2000、midas civil等均可方便进行线性、非线性时程分析。

影响时程分析结果因素较多，诸如地震动输入、材料特性、结构的阻尼、边界条件模拟等且均存在一定变异特性，而地震动输入对桥梁非线性时程分析结果影响最大[1]。我国由于强地面运动观测数据较缺乏，而场地地震安全性专项评估仅针对较重要工程项目进行，因此大多进行时程分析时往往采用个别典型的强震记录，如天津波、El Centro波等。虽时程分析为较准确的地震反应分析方法，但其准确性仅针对某一固定地震波而言[2]。地震波受震源、场地特性、传播介质等多因素影响，不确定性较大。不同地震波差异较大，即使在同一台站观测的不同时间段地震波也会极不相似[3-4]。采用不同地震波所得时程分析结果往往差异巨大[5-6]。如何选择合适的地震动输入成为提高时程分析准确性基础。

我国建筑、桥梁抗震设计规范均规定时程分析结果不小于反应谱计算结果的80%，此为时程分析应拟合反应谱的基本原则。本文在此基础上，结合地震波特性及结构动力分析基本原理，提出双参数选波原则，并经大量计算对几种地震波调整方法进行对比分析，给出实用且能降低时程分析结果离散性的地震波选择及调整方法。

1双参数地震波选择方法

1.1参数桥梁自振周期第一对比区间

据有阻尼体系的简谐荷载反应计算原理[7]，以单自由度体系为例，简谐荷载作用下体系的运动方程及初始条件为

(1)

其全解为

u(t)=uc+up=[e-ζωnt (Acos(ωDt)+Bsin(ωDt))]+

[Csin(ωt)+Dcos(ωt)]

(2)

由式(2)知，在简谐荷载作用下，体系振动由瞬态反应uc与稳态反应up两部分组成。瞬态反应项会在阻尼作用下较快衰减，系统振动仅剩稳态部分，即

u(t)=up=u0sin(ωt-φ)

(3)

式中：

(4)

将式(4)中ω/ωn定义为频率比，即外荷载激振频率与结构自振频率之比。将结构稳态反应振幅与结构等效静位移之比定义为结构位移放大系数，则动力放大系数为

(5)

由式(5)知，动力放大系数仅与结构阻尼、频率比有关。钢筋混凝土桥梁结构常用阻尼比为0.05的结构动力放大系数见图1。由图1看出，当荷载频率ω与结构体系基频ωn之比趋近于1时，体系发生共振反应。因此，在ω/ωn=1的附近区间，是体系输入荷载最应受关注的频段区间。本文据Rd-ω/ωn曲线覆盖范围，将动力放大系数Rd控制在2.0附近，以此为原则，将ω/ωn关注区间确定为结构自振周期的-30%~20%之间。

图1　结构动力放大系数示意图 Fig.1 Schematic diagram of the structure dynamic magnification factor

按桥梁抗震设计原理，能力保护设计原则和延性设计已深入人心。对普通桥梁而言，常通过桥梁墩柱的延性变形获得桥梁对大震的抵御能力。即桥梁结构在大震作用下，墩柱构件易遭不同程度损伤，如截面开裂、主筋屈服等，导致桥墩刚度退化，桥梁结构自振周期延长，亦即结构自振频率ωn变小，频率比ω/ωn变大。由此可将关注区间适当拓展至ω/ωn=0.7-1.3之间，并定义为低频段对比区间，见图2。

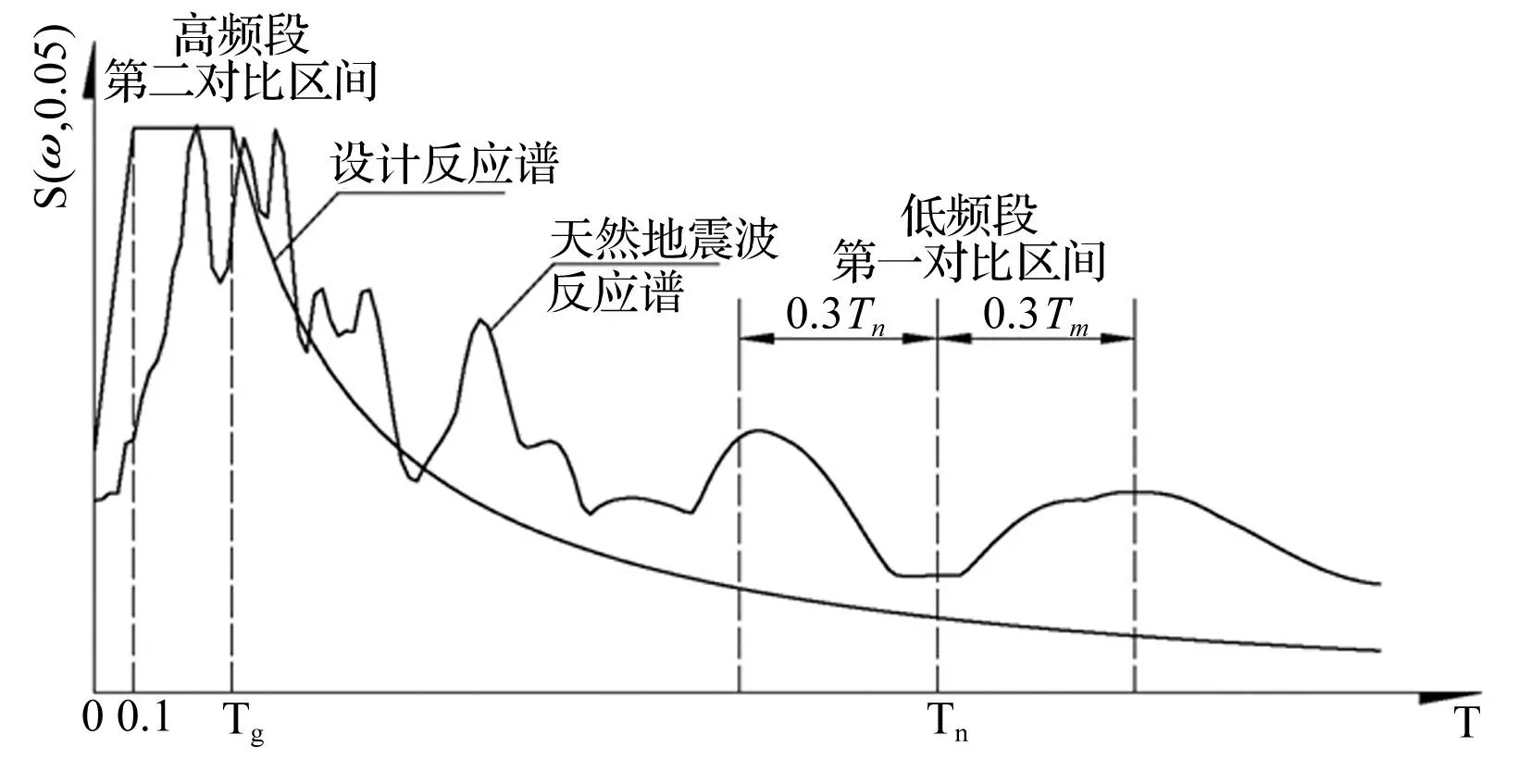
图2　天然地震波调整区间 Fig.2 The correction interval of natural seismicrecord

1.2参数反应谱高频段第二对比区间

目标反应谱通常有明显的峰值区间，我国桥梁抗震细则设计反应谱峰值区间为由0.1 s至特征周期Tg。Tg大小与桥梁所在场地有关，场地的剪切波速越大其特征周期越小，反之亦然。据反应谱定义，规范设计谱实际是结构不同周期与绝对加速度最大反应量的关系曲线。因此，除对比结构自振周期低频段第一对比区间外，反应谱峰值段尤其重要。故将该区间定义为高频段第二对比区间(图2)。

2天然地震波选择方法

人工合成地震波时总希望其转换的反应谱型与目标谱尽量一致[8]，而改进的人工地震波合成方法在目标谱上设置多个对比点进行误差分析及调整[9-10]。由于天然地震波形千变万化，虽已建立地震波数据库，但要寻找与目标谱型误差控制在较小范围内的天然地震波几乎不可能[11]。而强震数据库(PEER Strong Motion Database)[12]可据地震波反应谱进行筛选，设定反应谱加速度最大值、最小值，周期最大值、最小值作为天然地震动的初筛阶段。为保证所选地震波谱型与目标谱型一致，将反应谱曲线与横坐标(周期坐标)所围面积作为表征反应谱参数。据两个对比区间将目标谱0.1 s~Tg包围的面积ST1及0.7Tn~1.3Tn包围的面积ST2作为对比参数，天然波0.1 s~Tg包围的面积定义为SN1与0.7Tn~1.3Tn包围的面积定义为SN2，合格天然地震波的判定准则为

(6)

式中：

KT=ST1/ST2,KN=SN1/SN2

(7)

式(6)的含义为目标谱与天然地震波反应谱高频段所围面积与低频段所围面积的比值差异在±20%之间，以此控制两个对比区间天然地震波反应谱与目标谱型的符合性。

3时程分析中输入地震动选取

3.1桥梁结构参数

以常用的4跨先简支后连续T型梁桥为研究对象，其结构简图见图3。

图3　桥梁结构简图 Fig.3 Diagram of bridge structure

分析模型选桥梁工程中常用结构形式，4×30 m先简支后连续预应力混凝土T型梁桥,桥宽12 m。单跨桥梁由6片T型梁组成，单梁宽2 m，高2 m，质量85 t。桥梁下部构造为框架式桥墩，重力式U型桥台。桥台采用GYZF4 450x89型圆形四氟滑板式橡胶支座，桥墩采用《公路桥梁高阻尼隔震橡胶支座》(JT/T 842-2012)中推荐的HDR(Ⅰ)-d445×186型高阻尼橡胶支座。在桥墩顶底局部区域建立纤维模型进行动力弹塑性分析。以墩柱圆心做同心圆划分纤维，钢筋用Park模型、混凝土用mander模型模拟，并采用滞回系统模拟高阻尼橡胶支座及滑板支座，见图4。

图4　弹塑性纤维墩柱模型 Fig.4 Model of elasto-plastic fibre column element

桥梁拟建场地为8度0.2 g，Ⅱ类场地，反应谱特征周期Tg为0.45 s，反应谱峰值加速度按规范取值0.765 g。计算获得桥梁第一阶振型质量参与系数为0.902，周期为1.30 s，说明算例桥梁的第一阶纵桥向模态为主要模态。

3.2输入地震动选取

利用美国太平洋工程地震研究中心PEER数据库及反应谱筛选条件进行筛选，设定谱加速度最大值、最小值，初步筛选出50条天然地震波，绘制加速度反应谱曲线图，利用式(6)进行数据对比分析，最终筛选出7条符合要求的天然地震动波，见表1。反应谱曲线见图5(a)。

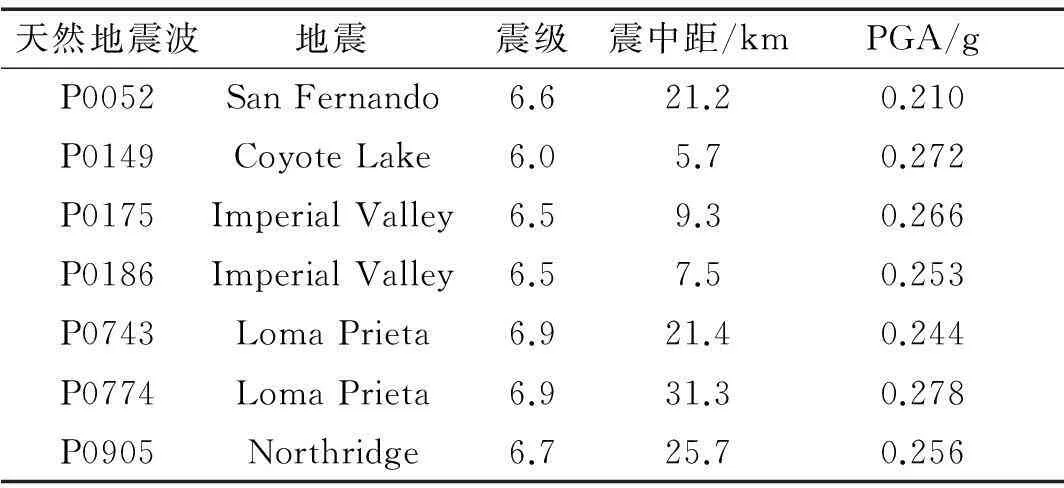
表1　所选天然地震波基础资料

据式(6)、(7)对天然地震波反应谱曲线进行量测，测出两个对比区间对应的面积，计算结果见表2。由表2看出，所选7条天然地震波基本能满足式(6)要求的±20%偏差。

表2　天然地震波选择依据

4输入地震动调整方法

4.1输入地震动调整

对输入地震动调整即为使地震动记录尽量与目标谱型一致。据反应谱曲线中两重要参数，存在5种不同调整方法。计算调整系数时所需天然地震波反应谱各控制点谱值与计算所得调整系数见表3。不同调整方法调整后反应谱曲线及均值反应谱见图5。

(1)调整方案1。据反应谱曲线两对比区段面积进行调整。通过设定调整系数使天然地震波在两区段的反应谱面积尽量接近目标谱面积，利用面积相等确保天然波谱型与目标谱型一致。调整参数K1的计算式为

(8)

(2)调整方案2。据桥梁周期点反应谱取值进行调整。即天然地震波反应谱在桥梁周期点的谱值与目标谱谱值一致。如本文算例的天然波在桥梁周期点1.3s处反应谱值与目标谱值一致，对比计算获得调整系数K2。

(3)调整方案3。据反应谱曲线第二对比区间(低频段)均值进行调整。本文目标谱峰值平稳段为0.91~1.69 s，设定对比控制点为低频段起点0.91 s、周期点1.30 s、终点1.69 s，获得天然地震波在3个点的谱值，计算平均值，与目标谱周期点1.30 s处谱值对比计算获得调整系数K3。

(4)调整方案4。据目标反应谱曲线峰值平稳段中点取值进行调整。如本文桥梁即为天然波在峰值中点0.275s处反应谱值与目标谱值一致，对比计算获得调整系数K4。

(5)调整方案5。据反应谱曲线第一对比区间(高频峰值段)均值进行调整。本文目标谱峰值平稳段为0.1-~0.45 s，设定对比控制点为平稳段起点0.1 s、中点0.275 s、终点0.45 s，获得天然地震波在3点谱值，计算平均值，与目标谱0.275 s处谱值对比计算获得调整系数K5。

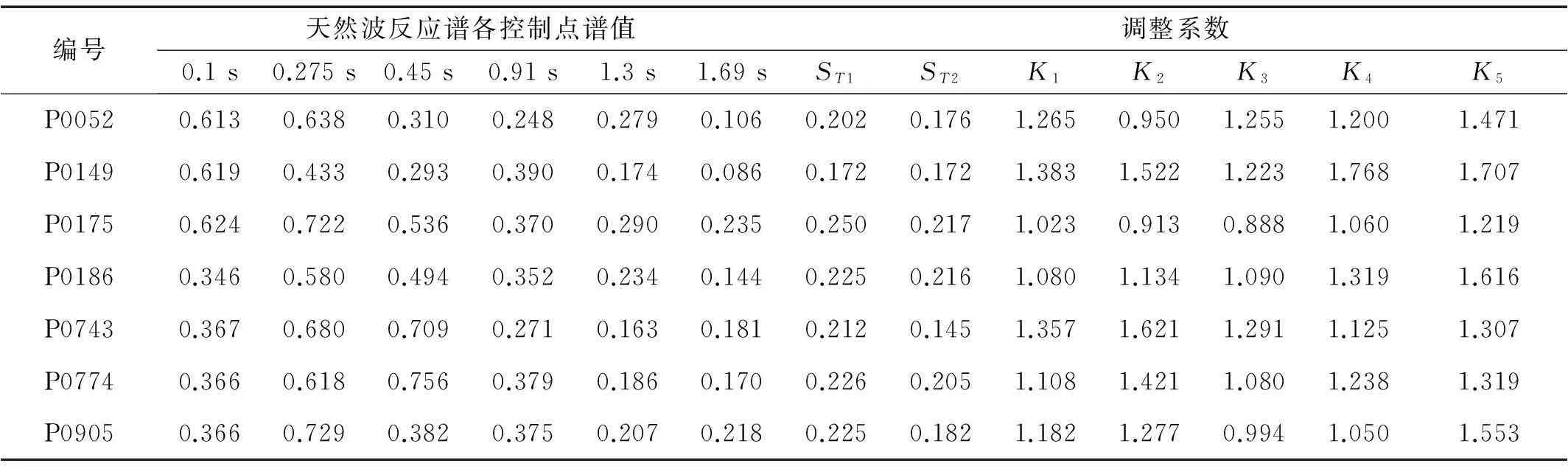
表3　所选天然地震波调整参数

表4　桥梁地震响应结果统计表

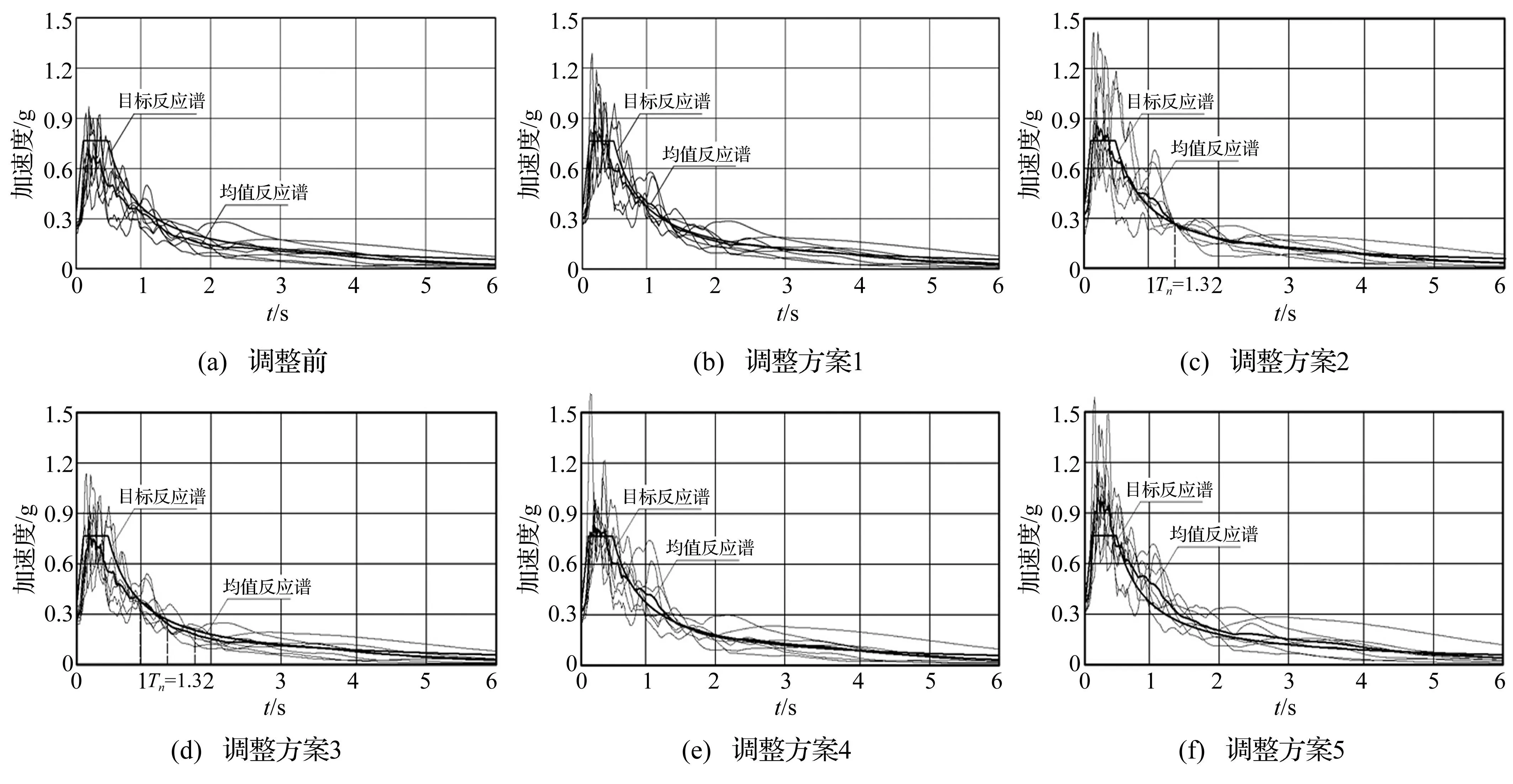
图5　调整后天然地震波反应谱 Fig.5 Response spectrum of adjusted natural seismic wave

4.2五种调整方案桥梁地震动响应统计

本文以5种调整方法所得地震波为地震动输入计算桥梁结构响应。以桥墩反应为研究对象对桥梁进行动力弹塑性分析，分析桥墩墩底弯矩、墩底剪力及墩顶位移，结果见表4。用墩底弯矩、剪力、墩顶位移变异系数(μ/σ)作为判定地震波调整方法的优、劣，变异系数越大说明计算结果越离散；变异系数越小说明计算结果越一致。时程分析结果离散性得到控制，计算才会可靠。

分析5种方法调整后的天然地震波时程分析结果中内力部分，其偏差系数均能控制在20%以内，说明本文以两个对比区间的反应谱面积作为选波基本参数、以目标谱及天然地震波反应谱高频段所围面积与低频段所围面积比值差异±20%是合理、有效的。同时说明用反应谱型对比选择地震波的基本原理合理。从不同对比参数分析，结构内力偏差系数明显小于结构位移偏差系数，主要与桥梁结构支座的非线性及结构自身变形的非线性有关。

由表4结果看出，采用方案1，用反应谱高频及低频两对比区段面积作为对比基数，综合调整后天然地震波，其计算结果离散性最小。调整方案2、3均用低频对比区间中周期点、周期均值进行调整，偏差系数稍大，且两方案的离散性较接近。方案4、5均用高频段对比区间中峰值中点及峰值平均值为基数进行调整，偏差系数明显大于方案1~3。由于天然地震波在峰值区域，其自身谱值变化较大，导致某特定点谱值与目标谱值偏差较大，此为采用峰值调整方法计算结果偏差较大的主要原因。而低频段，天然波反应谱值与目标谱值偏差较小(图5)。5种反应谱调整方法对比，采用方案1面积调整，偏差系数最小，说明采用反应谱曲线面积作为基本参数对反应谱型的一致性进行判定是有效的。

5结论

为保证桥梁地震动时程分析结果的可靠性，选择合适的地震波最关键。若要求天然地震波在各周期与目标谱均具有较高的一致性，则选波工作困难较大甚至不可能完成。本文通过分析规范规定目标谱型特点，采用双参数对比选波及调整方法，并进行数值分析，结论如下：

(1)结合结构动力放大系数的基本原理及地震波能量原理，通过分析反应谱谱型特点，将反应谱型拟合归纳为两个重要区间，即将结构自振周期±30%范围作为低频对比区间、规范0.1 s~Tg范围作为高频对比区间作为选波的控制参数。

(2)用反应谱曲线所围面积衡量反应谱曲线的拟合程度合理、有效。以目标谱、天然地震波反应谱高频段所围面积与低频段所围面积比值差异为±20%，该幅值既能降低选波难度，亦能控制时程分析结果的离散度。

(3)据反应谱曲线两对比区段面积进行调整，通过设定调整系数，使天然地震波在两区段的反应谱面积尽量接近目标谱面积。调整后的天然波反应谱与目标谱型一致性最高，其时程分析结果离散系数控制在10%~20%之间，内力离散性远小于位移的离散性。

参考文献

[1]Lee T H, Mosalam K M. Probabilistic seismic evaluation of reinforced concrete structural components and systems[R]. Pacific Earthquake Engineering Research Center, University of California, Berkeley, CA.，2006.

[2]朱东生,劳远昌,沈大元,等.桥梁地震反应分析中输入地震波的确定[J]. 桥梁建设, 2000,3:1-4.

ZHU Dong-sheng, LAO Yuan-chang, SHEN Da-yuan,et al. Determination of seismic waves introduced into bridge seismic response analysis[J]. Bridge Construction, 2000, 3: 1-4.

[3]王亚勇, 程民宪, 刘小弟. 结构抗震时程分析法输人地震记录的选择方法及其应用[J].建筑结构学报, 1992,2(5):3-7.

WANG Ya-yong, CHENG Ming-xian, LIU Xiao-di. Method and application for choosing input seismic recording in structural seismic time history analysis method[J]. Journal of Building Structure,1992,2(5):3-7.

[4]杨溥, 李英民, 赖明. 结构时程分析法输入地震波的选择控制指标[J]. 土木工程学报, 2000, 33(6):33-37.

YANG Pu, LI Ying-min, LAI Ming. A new method for selecting inputting waves for time-history analysis [J]. China Civil Engineering Journal, 2000, 33(6):33-37.

[5]樊剑,余倩倩,邵丹. 地震波随机模型对隔震结构地震需求分析的影响[J]. 振动工程学报, 2011, 24(4): 412- 420.

FAN Jian, YU Qian-qian, SHAO Dan. Effect of nonstationary stochastic model of earthquake records on the probabilistic seismic demend analysis of base isolated structures[J]. Journal of Vibration Engineering, 2011,24(4):412-420.

[6]杨红,吴晶晶. 考虑结构局部反应特征的时程分析法输入地震波研究[J]. 土木工程学报, 2007, 40(11): 29- 35.

YANG Hong, WU Jing-jing. A study on the earthquake input for time-history analysis based on the local response characteristics of structures [J]. China Civil Engineering Journal, 2007, 40(11):29-35.

[7]刘晶波，杜修力. 结构动力学[M].北京:机械工业出版社,2007.

[8]翟希梅，吴知丰. 人工地震波反应谱拟合技术的改进[J]. 哈尔滨工业大学学报，1995,27(6):130-133.

ZHAI Xi-mei, WU Zhi-feng. Improvement in the fitting technology of response spectra for simulated earthquake wave[J]. Journal of Harbin Institute of Technology,1995,27(6):130-133.

[9]李建华,李杰. 考虑反应谱变异特性的人工合成地震波[J]. 同济大学学报,2002,30(9):1038-1043.

LI Jian-hua, LI Jie. Simulation of ground motions considering variability of response spectra [J]. Journal of Tongji University，2002,30(9):1038-1043.

[10]吴昊，张洵安. 基于HHT方法的非平稳人工地震动模拟[J].地震工程与工程振动,2011,31(6):30-37.

WU Hao，ZHANG Xun-an. Simulation of non-stationary artificial seismic ground motions based on HHT theory [J]. Journal of Earthquake Engineering and Engineering Vibration, 2011,31(6):30-37.

[11]邹立华, 刘爱平, 杨宏,等. 利用小波重构合成地震波方法及特性研究[J].地震学报,2007,29(6):635-642.

ZOU Li-hua, LIU Ai-ping, YANG Hong,et al. Characteristics and method of synthesis seismic wave based on wavelet reconstruction[J]. ACTA Sesmologica Sinica, 2007,29(6):635-642.

[12]李琳, 温瑞智, 周宝峰,等. 基于条件均值反应谱的特大地震强震记录的选取及调整方法[J]. 地震学报, 2013, 35(3):361-370.

LI Lin, WEN Rui-zhi, ZHOU Bao-feng,et al. Selection and scaling of ground motion records for great scenario earthquakes based on conditional mean spectrum [J]. ACTA Sesmologica Sinica, 2013, 35(3):361-370.