舰载共架垂直发射导弹发射时间协调
2016-01-06贾正荣,卢发兴,吴玲
舰载共架垂直发射导弹发射时间协调
贾正荣,卢发兴,吴玲
(海军工程大学 电子工程学院,武汉 430033)
摘要:为了避免发射和飞行中2枚导弹的相互干扰,研究了共架垂直发射导弹的发射时间协调,基于垂直发射导弹发射初始段的运动特性,考虑垂直上升段和程序转弯段的弹道散布误差,建立了弹道散布体时域模型;引入距离裕度的概念,对不同发射时刻下2枚导弹的预定弹道管道进行冲突检测,并根据距离裕度确定导弹发射间隔时间。仿真结果表明,得到的冲突检测与消解的时间在100 ms级,满足实战要求。
关键词:舰空导弹;垂直发射;发射时间;冲突检测;冲突消解
收稿日期:2014-06-11
作者简介:贾正荣(1992-),男,硕士研究生,研究方向为舰载武器控制系统。E-mail:jzr451763650@sina.cn。
中图分类号:TJ761文献标识码:A
LaunchTimeCoordinationforShip-borneCommon-frame
VerticalLaunchMissile
JIAZheng-rong,LUFa-xing,WULing
(CollegeofElectronicEngineering,NavalUniversityofEngineering,Wuhan430033,China)
Abstract:To avoid the interference of two missiles at the launch and flight processes,the launch-time coordination for ship-borne common-frame vertical-launch missiles was analyzed.Based on the initial motion feature of the vertical-launch missile,the time-variable trajectory distribution model was established in view of the trajectory dispersion-errors during vertical ascent phase and procedure turn phase.By introducing the distance-margin,the potential conflict of two missiles’ trajectory pipes of different launch time was detected,and the launch interval was obtained.The simulation result shows that time-consuming of the whole process is confined within 100 milliseconds,and it can meet the requirements of combat.
Keywords:ship-to-airmissile;verticallaunching;launchtime;conflictdetection;conflictresolution
共架垂直发射是舰载导弹的一种重要发射方式。发射协调是共架武器发射控制的重要环节,它是在通用发控单元同时收到多个导弹发射命令时,为避免发射和飞行中两弹的相互干扰,而协调导弹的发射弹位、空域、发射时间的过程。其中发射时间协调可以在发射弹位和空域协调的基础上,进一步消除发射装置振动、燃气排导、初始弹道交叉等的影响,因而是协调的关键。时间协调需要解算两弹的预定弹道交叉点和前一枚弹飞过弹道交叉点的时间,来确定后一枚弹的发射时间。相关文献中针对火力交叉判断的研究较多[2-4],但不涉及发射延迟时间的计算,而且大多是通过计算2条弹道的静态距离来判断交叉,其结果与不同发射时刻下的动态飞行情况不符,容易造成误判;此外,考虑误差影响时弹道呈管道形式,难以求交叉点,需要在合理表示冲突区域的基础上进行发射时间协调。
本文在建立导弹发射初始段运动模型和弹道散布体时域模型的基础上,引入距离裕度的概念,为不同发射时刻下2枚导弹的预定弹道管道进行冲突判断,确定冲突时刻,从而在距离裕度为正的原则下确定导弹发射间隔时间,实现共架垂直发射的时间协调。
1垂直发射导弹初始段运动模型
舰载垂直发射导弹的外弹道按照运动阶段可以分为垂直上升段、程序转弯段与制导飞行段,如图1所示。共架发射导弹的时间协调仅涉及导弹的初始段,即垂直上升段与程序转弯段。
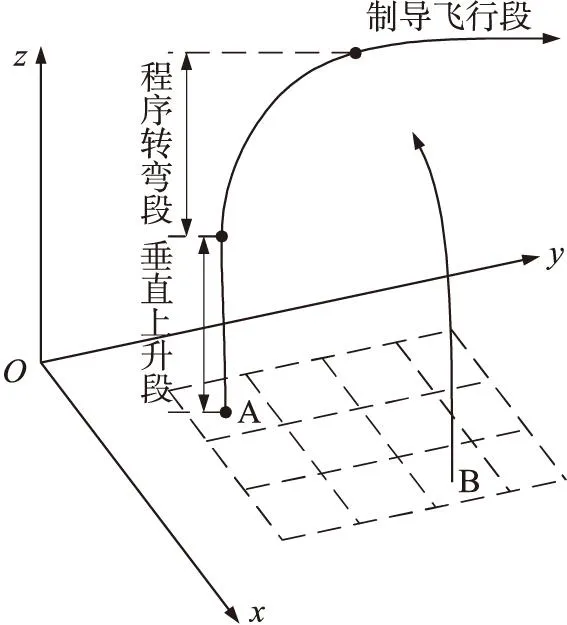
图1 单个舰艇平台多枚垂直发射导弹弹道示意图
考虑冷发射方式建立垂直发射导弹垂直上升段和程序转弯段的运动模型。为了降低模型复杂度且不影响问题的本质,将导弹视为质点。冷发射方式下导弹首先通过压缩气体或机械装置获得初速,在空中无动力飞行一段时间(t0≤t≤t1a)。这时导弹仅受空气动力以及重力的作用,在惯性直角坐标系中,其运动方程可以表示为
(1)
在无动力飞行段,可以认为作用在导弹弹体上的力矩为0,这样,导弹俯仰角ε和偏航角β均为定值,其运动仅与发射时的初速度、初始俯仰角及初始偏航角有关。
无动力飞行段之后导弹进入助推器工作段(t1a≤t≤t1),为简化分析,可以从助推器提供的加速度而不是提供的动力方面考虑,此外,认为导弹质心位置固定,此时得到助推器工作段导弹的运动模型:
(2)
式中:ap为导弹助推器提供的加速度,g为重力加速度。
经过垂直上升段的加速过程,导弹进入程序转弯段(t1≤t≤t2),导弹调整自身姿态以对正目标提前点,此阶段受力过程复杂,本文仅给出运动方程:
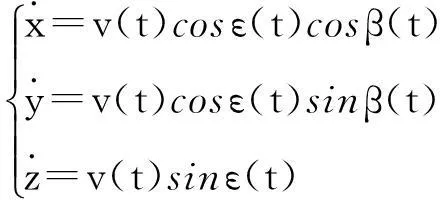
(3)
式(3)中导弹速度、俯仰角以及偏航角是变化函数,导弹对这3个变量要进行控制。对于俯仰通道的控制,其时域形式可表示为
(4)
式中:ε0为俯仰角初值,εe为转弯终点俯仰角即控制目标,τs为时间系数(调节时间);Ks为控制系数。偏航通道与速度通道的控制类似式(4)给出。
2垂直发射导弹弹道散布
导弹在发射后的实际运动过程中可能受到各种外界干扰,同时,导弹运动参数与理论值也会存在一定的偏差,这些因素共同作用使得导弹的实际弹道呈现一定的散布。为了与导弹运动模型相结合,可以认为导弹的运动参数存在误差,造成弹道散布的误差在导弹运动的各个阶段有所不同,如图2所示。

图2 垂直发射导弹初始段运动参数误差示意图
2.1 垂直上升段误差
冷发射的垂直上升段,弹射装置提供给导弹的初速度会存在一定的误差,称为发射初速度误差Δv0,该误差产生的原因与机械装置有关,可以认为其服从正态分布,并且会对导弹的弹道造成一定的影响。
另外,舰艇在海面上运动,其甲板面会与水平面存在一定的倾角,而弹仓又是固连在舰艇上的,所以导弹发射时的姿态角也会存在一定的误差,即发射角度误差Δε0,该误差是实际的发射姿态角与理论发射姿态角的偏差。
Δv0和Δε02个误差均出现在导弹弹射出仓的时刻,是导弹运动初始状态的误差,不改变导弹的运动模型,并且在无动力飞行段,导弹不修正自身的姿态,所以Δv0和Δε0在无动力飞行段是不变的。在助推器工作段,导弹会通过传感器测量自身的姿态并予以修正,此时,误差会按照一定的规律衰减,设误差为δ,其衰减规律可以用负指数函数描述:
(5)
式中:δ0为误差初值,Kd为衰减系数,τd为衰减时间。
2.2 程序转弯段误差
程序转弯段是导弹进行姿态调整的阶段,由于动力过程复杂,可以通过运动参数的误差来估计其弹道散布。根据式(3)描述的导弹程序转弯段运动方程,此阶段共有速度、俯仰角与偏航角3个运动参数。首先,导弹在进入程序转弯段时,其运动状态与理论值会存在一定的偏差;其次,在进行姿态调整的过程中,由于控制系统并不是理想的,控制过程也会存在一定的误差。综合来看,可以认为是导弹在进入程序转弯段时的运动状态存在误差,导致整个程序转弯段产生弹道散布。
综上所述,程序转弯段中的运动参数误差包括转弯初速度误差Δvt,俯仰转向误差Δεt与偏航转向误差Δβt。类似地,程序转弯段中的运动参数误差也会依照式(5)衰减。
值得注意的是,上述误差均为系统误差,导弹在运动中还会受到各种随机扰动的影响,这些扰动呈现一定的统计特性,在计算中可以通过增大弹道散布的方法来覆盖这些扰动。
2.3 弹道散布体模型
由于导弹的运动模型较为复杂,其每一时刻的弹道散布难以得到解析的形式,此时可建立散布体模型以包络实际的弹道散布。本文建立散布球体模型。
设t时刻导弹可能出现的位置为pi(x,y,z,t),p0(x,y,z,t)为理论弹道此时的位置,定义di(t)表示t时刻导弹实际位置与理论位置的偏差,即
di(t)=|pi(x,y,z,t)-p0(x,y,z,t)|i≠0
(6)
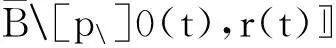

图3 弹道散布表示方法示意图
只要给出r(t)表达式,即得到弹道散布球体模型。下面按导弹的运动阶段分别计算r(t)。在自然坐标系中,带有误差的弹道会产生沿着理论弹道的切向误差Δσ和垂直于理论弹道的法向误差Δn。
这样,散布球体半径就可以通过切向误差与法向误差来描述:
(7)
在垂直上升段的无动力飞行段,运动参数误差Δv0与Δε0造成的散布球体半径为
(8)
在垂直上升段的助推器工作段,考虑误差衰减的散布球体半径为
(9)
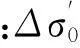
在程序转弯段,考虑误差衰减的散布球体半径为
(10)
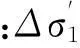
3共架垂直发射时间协调
建立的导弹散布球体模型反映了导弹在每时刻可能出现的区域。只要判断2枚导弹在同一时刻的散布球体是否存在交集就可以判断弹道是否可能产生冲突。
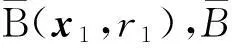
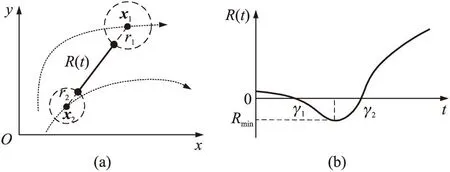
图4 距离裕度示意图
注意到,上述方法是将导弹当作质点处理,如果考虑导弹初始运动段姿态变化剧烈,更为保守的方法是进一步考虑导弹的实际尺寸,此时可对散布球体半径作如下处理:
r′=r+l
(11)
式中:r为导弹的散布球体半径,l为导弹的半长(考虑导弹质心位置)。

定义2发射协调规则:在闭区间[t0,t2]上,当Rmin>0时,无空域冲突;当Rmin≤0时,存在空域冲突,需要进行发射时间协调。此时,将优先级低的导弹延迟td时间发射,使协调后的距离裕度满足Rmin>0。
由于R(t)形式复杂,难以求取最优的发射间隔时间,所以采用迭代的方法求取较优的发射间隔时间。当考虑发射间隔时间后,R(t)变为R(t,td),并且有
式中:λ为控制系数,给定e>0,当|td,i-td,i+1|
利用发射协调规则进行发射时间协调,过程如图5所示。
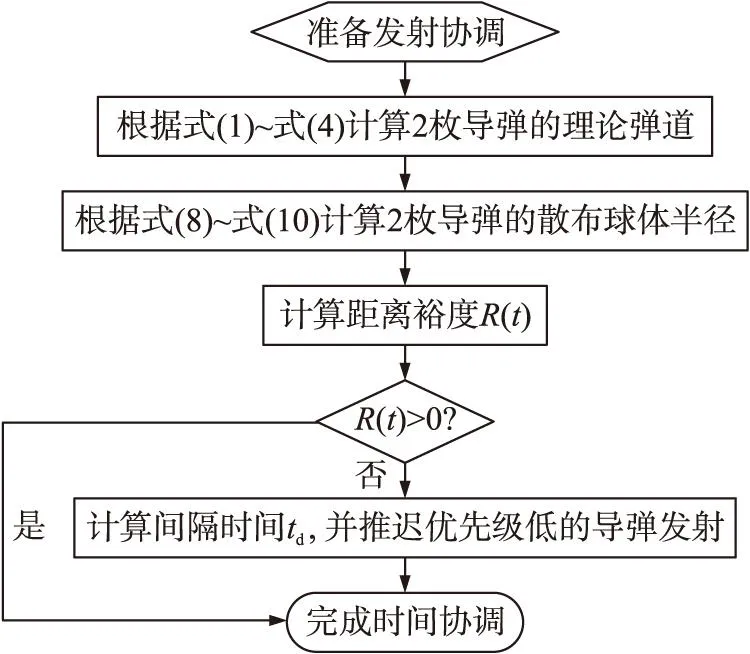
图5 发射时间协调流程图
4算例分析
共架垂直发射导弹A与导弹B需要进行发射时间协调。设导弹A发射优先级较高。算例中不考虑导弹实际尺寸。
导弹A位于(0,0,0)处,冷发射,发射初速20 m/s,无动力飞行时间2 s;助推器提供加速度11g,助推器工作3 s,转弯终点俯仰角30°,偏航角60°;速度通道调节时间2 s,偏航通道调节时间2 s,俯仰通道调节时间1.5 s。
导弹B位于(0,5,0)处,冷发射,发射初速20 m/s,无动力飞行时间2 s;助推器提供加速度11g,助推器工作3 s;转弯终点俯仰角40°,偏航角40°;速度通道调节时间2 s,偏航通道调节时间2 s,俯仰通道调节时间1.5 s。
导弹运动参数误差取3组大小不同的值,如表1所示。

表1 运动参数误差取值
根据式(1)~式(4),仿真得到的2枚导弹理论弹道如图6所示。

图6 垂直发射导弹理论弹道
根据式(8)~式(10),仿真得到的弹道散布球体半径如图7所示,图中t=5 s对应虚线表示程序转弯段开始时刻。

图7 导弹散布球体半径
3组误差取值下,取λ=0.1,采用四阶Runge-Kutta法,步长恒定为0.02 s时协调过程的计算耗时(包括导弹A的弹道与弹道散布计算耗时tA,导弹B的弹道与弹道散布计算耗时tB,距离裕度与发射间隔时间的计算耗时tC,及计算共用时tM),得到的间隔发射时间td如表2所示,3组误差通过不同的λ得到的发射间隔时间如表3所示。根据表2中计算得到的发射间隔时间进行发射协调前后的距离裕度如图8所示。

表2 时间协调计算耗时(运动参数误差不同)

表3 选取不同λ计算得到的发射间隔时间
由表3可知,λ的取值过大会导致计算得到的间隔时间过长。
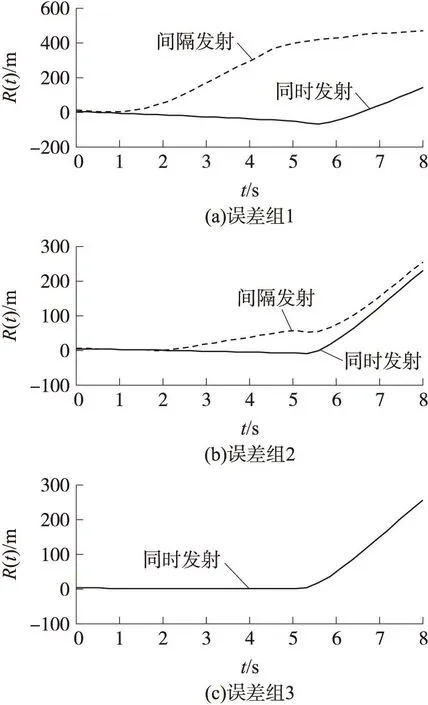
图8 不同发射时间对应的距离裕度
由图8可知,运动参数误差增大会使导弹冲突的可能性加大,利用计算发射间隔时间可以有效避免垂直发射导弹的初始弹道冲突,并为共架垂直发射导弹时间协调提供依据。而整个协调过程的计算耗时在100 ms级,可以满足任务的实时性要求。
5结束语
本文研究了舰艇共架垂直发射导弹的时间协调问题,建立了导弹发射初始段运动模型和弹道散布体时域模型,在距离裕度为正的原则下确定发射间隔时间,避免导弹在初始弹道段的冲突。由仿真结果可以看出,该方法可有效地对初始弹道冲突进行定量判断和发射时间协调。模型和方法还可为舰载武器火力兼容判断提供定量分析依据。
参考文献
[1]刘方,辜健,邱志明,等.基于公共燃气排导结构的发射系统武器选择与布局方法.海军工程大学学报,2012,24(2):53-56.
LIUFang,GUJian,QIUZhi-ming,etal.Methodsofweaponselectionandlayoutincommon-framelaunchsystembasedonpublicexhaustlauncher.JournalofNavalUniversityofEngineering,2012,24(2):53-56.(inChinese)
[2]桂秋阳,邱志明.基于垂直发射武器的火力交叉判断模型.兵工学报,2008,29(11):1 373-1 378.
GUIQiu-yang,QIUZhi-ming.Modeloftheestimationoffireintersectionbasedonverticallaunchweapons.ActaArmamentarii,2008,29(11):1 373-1 378.(inChinese)
[3]王义涛,王超.编队协同防空作战中的火力兼容判断研究.现代防御技术,2010,38(4):53-56.
WANGYi-tao,WANGChao.JudgingoffirecompatibilityinwarshipsformationcooperativeantiairModernDefenceTechnology,2010,38(4):53-56.(inChinese)
[4]姚跃亭,赵建军,杨利斌,等.弹道预测下的舰艇编队防空火力冲突判定.弹道学报,2011,23(2):47-51.
YAOYue-ting,ZHAOJian-jun,YANGLi-bin,etal.Predicationoffirepowerconflictinfleetair-defensebyballisticestimation.JournalofBallistics,2011,23(2):47-51.(inChinese)
[5]孟海东,廖洪昌,郭荆燕,等.飞航导弹齐射发射时间的一种快速规划算法.火力与指挥控制,2009,34(9):106-113.
MENGHai-dong,LIAOHong-chang,GUOJing-yan,etal.Anfastprogrammingarithmeticoflaunchtimewhenmanywindedmissilesarelaunchedsynchronously.FireControlandCommandControl,2009,34(9):106-113.(inChinese)
[6]高帆,李向林.垂直发射近程防空导弹全方位快速转弯技术研究.现代防御技术,2009,37(6):18-21.
GAOFan,LIXiang-lin.Vertical-launchshort-rangeairdefensemissile’sall-directionrapidturntechniquestudy.ModernDefenceTechnology,2009,37(6):18-21.(inChinese)