拦截临近空间飞行器零控脱靶量计算方法

拦截临近空间飞行器零控脱靶量计算方法

李罗钢1,2,荆武兴1,高长生1

(1.哈尔滨工业大学 航天学院,哈尔滨 150001;2.中国运载火箭技术研究院 研发中心,北京 100076)

摘要:为精确预测拦截高速飞行的临近空间飞行器时的零控脱靶量,根据拦截临近空间飞行器的特点对拦截弹及目标飞行器动力学模型进行了合理简化,推导了拦截弹与目标飞行器相对运动状态解析表达式,得出了一种具有较高精度的零控脱靶量解析计算方法。为验证该算法精度,建立了尽可能接近真实情况的动力学模型,并采用数值积分方法进行仿真对比,结果表明该算法精度较高。将该算法应用于一个简单的中制导律,证明了其在拦截临近空间飞行器时的可行性。

关键词:临近空间飞行器;拦截;中制导;零控脱靶量;解析解

收稿日期:2013-05-12

作者简介:李罗钢(1984- ),男,工程师,博士,研究方向为空间攻防对抗。E-mail:llg0315@sina.com。

中图分类号:TJ303.4文献标识码:A

Zero Effort Miss Formulation for Near Space Aircraft Interception

LI Luo-gang1,2,JING Wu-xing1,GAO Chang-sheng1

(1.School of Astronautics,Harbin Institute of Technology,Harbin 150001,China;

2.R&D Center,China Academy of Launch Vehicle Technology,Beijing 100076,China)

Abstract:To accurately predict the zero effort miss for intercepting the near space aircraft(NSA)with high velocity,three-dimensional simplified dynamic model was presented according to the characteristics of NSA,which was transformed into linear differential equation with constant coefficients.The analytic expressions of motion of interception missile relative to aircraft was deduced.The high-precision method of calculating zero effort miss was obtained.To verify the precision of the method,the dynamic model as close to the actual conditions as possible was built,and the comparison was carried out by numerical integration.The simulation results show that the analytical formula is feasible.The zero effort miss calculation was applied in a simple mid-course guidance law to verify the interception effect in engineering application.

Key words:near space aircraft;interception;mid-course guidance;zero effort miss;analytical solution

近年来,临近空间飞行器发展较快,对临近空间目标进行有效防御的研究具有重要战略意义。拦截弹飞行弹道一般包括飞行初段、飞行中段和飞行末段3部分,在飞行初段完成预设程序飞行后便进入飞行中段。拦截弹在飞行中段需要加入中制导,所以飞行中段又称中制导段[3-5]。

反导拦截中往往会遇到速度远快于拦截弹的目标,比如弹道导弹及临近空间飞行器。当拦截弹不具备速度优势时,以往用于拦截低速目标的制导方法便不再适用,因此,基于预测零控脱靶量(ZEM)的中制导理论应运而生。该方法通过实时预测ZEM,并采用制导指令对其进行实时调整,以实现对拦截弹的制导控制。因此,ZEM的预测计算成为中制导理论中必须解决的问题。

ZEM定义为拦截弹主发动机关机后目标和拦截弹只在非控制力的影响下滑行运动的最小相对距离。当拦截弹在空间某点的ZEM为0,即处于零控拦截状态时,则认为不加控制也能在有限时间内实现对目标的直接碰撞拦截。基于ZEM的中制导理论最早由Newman提出,并广泛应用于大气层外空间反导拦截领域。文献针对目标与拦截弹引力加速度差的几种简化模型,推导了相应的ZEM表达式,并进行了定量的精度分析;参考文献[10-11]得出一种具有较高精度的适用于大距离拦截的ZEM计算方法;文献[12]设计了适用于高轨道超远距离拦截的ZEM计算方法;文献[13]推导了适用于拦截螺旋机动弹道导弹的ZEM计算公式。

与拦截大气层外空间飞行器不同,临近空间飞行器本身具有一定借助稀薄大气进行机动的能力,且拦截弹也会受到稀薄大气的影响,因此其ZEM的计算也与前人的研究不同。本文针对拦截临近空间飞行器的具体特点,系统研究ZEM的计算方法。

ZEM的计算需要考虑计算速度和预测精度两方面因素。弹载计算机运算速度有限,因而要求ZEM在实战中必须首先实现快速计算。而ZEM的预测精度将直接影响到设计的中制导律能否为末制导段提供一个良好的初始环境。拦截弹和目标飞行器在飞行时受地球引力、稀薄大气作用等多种因素影响,一般情况下的零控脱靶量无法用解析表达式准确描述,只能采用相对简化的模型,以实现零控脱靶量的快速解析计算。因此,选取何种模型以平衡计算速度与预测精度的关系是需要深入研究的问题。

1临近空间飞行器简化模型

由于临近空间飞行器运动受稀薄大气影响,而且作为非合作目标,包括其气动参数在内很多信息都是未知的,因此无法像大气层外拦截那样准确建立目标动力学模型。所有已知信息只能通过探测手段获得,包括当前时刻位置矢量信息、速度矢量信息,及跟踪滤波得到的加速度矢量信息。

本文所要拦截的目标是一种临近空间无动力滑翔飞行器(以美国HTV-2为代表),采用乘波体结构。该类型飞行器可借助临近空间稀薄大气进行大范围横向机动,而且其速度受空气阻力影响随时间逐渐减小。本文根据该类型飞行器以上轨迹特性,研究采用变速率转弯模型模拟飞行轨迹。该模型将目标当前时刻加速度矢量信息分解为沿速度方向的纵向加速度和与速度方向垂直的横向加速度,并假设大小都不变。目标在横向做拟圆周运动,在纵向做匀减速运动,如图1所示。图中,R为飞行器位置矢量,o为当前时刻位置,v0为当前时刻速度矢量,az为纵向加速度,ah为横向加速度。

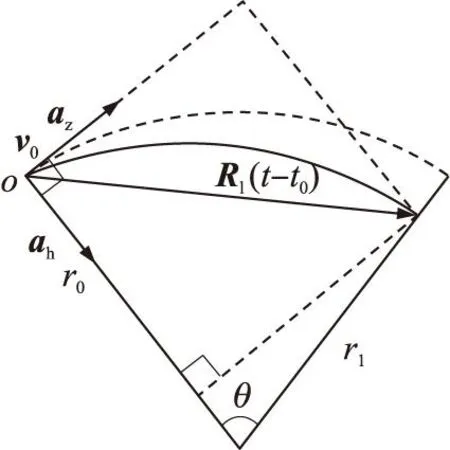
图1　目标飞行器模型

可以得到目标临近空间飞行器状态方程:

Rl(t)=Rl(t-t0)+Rl(t0)=

(1)

(2)

其中:

(3)

(4)

(5)

2拦截弹简化模型

主发动机关机后拦截弹仅受到重力及稀薄大气影响。本文假设拦截弹零控飞行弹道为零攻角转弯弹道,并将拦截弹的受力沿速度方向及位置方向进行分解,即沿速度反方向的空气阻力F,以及沿位置方向的重力加速度矢量g,如图2所示。

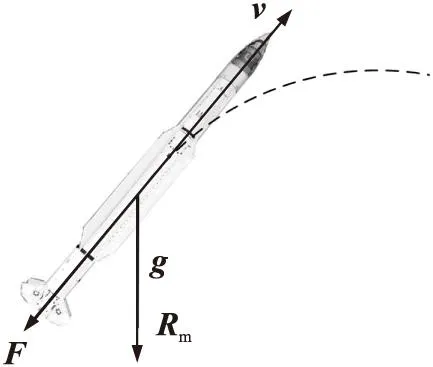
图2　拦截弹模型

拦截弹模型为

(6)

式中:Rm为拦截弹位置矢量,μe为地球引力系数。该模型是一非线性模型,需要对其进行简化。与大气层外拦截相比,临近空间拦截相对距离较小,拦截弹发动机关机后已基本达到临近空间飞行器作战高度。因此其自由滑翔时间也很短,末段高度变化仅数km级别,为地球半径的千分之一数量级,可以认为拦截弹位置矢量的模R为一常值。另外拦截弹主发动机关机后,末制导段时间很短,速度变化不大,可以假设拦截弹主发动机关机后空气阻力的大小为一常值。

Rm=Rm1=Rm0

(7)

(8)

式中:Rm1为拦截弹发动机关机点位置;vm1为拦截弹发动机关机点速度矢量的模;F1为拦截弹发动机关机点时刻空气阻力。这样一来,便可以得到拦截弹线性化的动力学模型,并可以转化为常系数二阶线性微分方程:

(9)

其中,

(10)

(11)

考虑到拦截弹发动机关机时距离地面高度约50km左右,末端速度一般在2 000～3 000m/s左右,而且临近空间大气稀薄,空气阻力较小,因此有:

(12)

(13)

因此可以得到s2-4n<0,通过Laplace变换可最终得到拦截弹状态方程解析解:

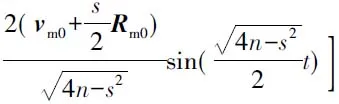
(14)

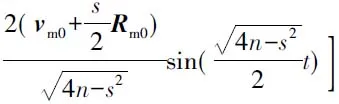
(15)

3零控脱靶量计算

根据式(1)和式(2)及式(14)和式(15),拦截弹与目标飞行器之间的相对位移及相对速度分别为

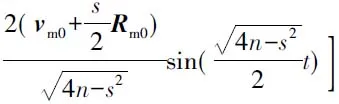
(16)

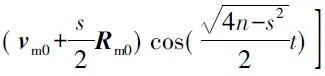
(17)

在零控脱靶时刻,有:

R·v=0

(18)

将式(16)和式(17)代入式(18),并做进一步简化,最终可以得到零控脱靶时间为

(19)

其中:

(20)

约束条件:

Δ=B2-4AC>0

(21)

其中:

(22)

其中:

(23)

式中:θ1是向量al与vm0的夹角;θ2是向量vl0与vm0的夹角;θ3是向量Rl0-Rm0与al的夹角;θ4是向量Rl0-Rm0与vl0的夹角;θ5是向量Rl0-Rm0与vm0的夹角。将式(19)带入式(16),得到零控脱靶量解析表达式:

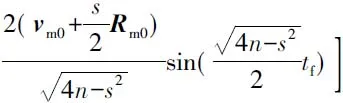
(24)

式中:tf代表拦截时刻。

4仿真算例

本节首先仿真验证前面得到的ZEM预测解析表达式的计算精度,然后将该ZEM预测方法应用于一个简单的中制导律,以验证该预测方法在拦截临近空间飞行器时的效果。

首先,给出的临近空间飞行轨迹要尽可能接近真实情况。假设目标飞行器初始时刻在经度0°、纬度0°位置上空50km处,地固系下坐标(6 428,0,0)(km)。初始时刻Ma约为15(模拟HTV-2),地固系下速度(0,5 000m/s,0),加速度测量信息(0,0,1.5g)。本文使用考虑J2项摄动的地球引力模型及标准大气模型模拟目标真实轨迹,目标飞行器动力学方程为

(25)

式中:g为考虑J2项摄动的地球重力加速度。

(26)

式中:μe为地球引力系数;J为地球扁率项;ae为地球椭球体长半轴;Ψ为地心纬度;m为质量;gw,gg分别为克里奥利加速度和牵连加速度;A1为地固系到弹体系的欧拉旋转;A2为速度系到弹体系的欧拉旋转;FN为作用在飞行器上的气动力。因无法得到目标飞行器气动参数,本文目标飞行器气动参数参考国外普通乘波体飞行器相关文献[14]。假设飞行器高度低于50 km时自动调整攻角,则飞行器在临近空间中进入了长距离滑翔阶段。另外给飞行器一常值侧滑角,实现5 000 km射程以及2 000 km侧向机动能力[15]。最终得到的接近真实情况的临近空间飞行器模拟轨迹如图3所示。

图3　飞行器轨迹

假设拦截弹初始时刻在约经度0.445°,纬度0.03°位置上空约47 km处(初始时刻距离目标飞行器约50 km),地固系下坐标(6 424.8,49.9,3.35)(km)。初始时刻Ma约为6,地固系下速度(370 m/s,-1 950 m/s,-390 m/s)。采用式(12)给出的相对距离计算方法,计算拦截弹与目标飞行器的实时相对距离信息。作为比较,本文结合动力学模型式(25),采用Matlab及Ode45积分器进行积分计算,以获得更加接近真实情况的实时相对距离信息并与式(16)对比。另外,在对比中还加入使用简化模型计算实时相对距离信息以进一步说明本文算法的优势。该模型假设目标飞行器做匀加速运动,拦截弹做匀速运动:

(27)

假设拦截弹不进行中段制导,采用上述3种方法预报拦截弹与目标飞行器的实时相对距离信息,预报结果如图4所示,其中,图4(b)是图4(a)的局部放大图。

图4　相对距离信息预报结果

零控脱靶发生时刻不同预测方法的ZEM精度如表1所示。表中,ZEM表示ZEM的值。

表1　零控脱靶量预测

由上面仿真结果可见,采用本文所提出的ZEM计算方法得到的解析预报结果与积分得到的真实结果相比,50 km相对距离上相差仅100 m左右,比简化模型的预报精度大为提高。

下面再用一个简单的算例来验证本文所提出的ZEM计算方法如何适用于临近空间拦截中制导。假设拦截弹过载制导指令:

(28)

表2　剩余零控脱靶量

由表2可见,采用本文提出的ZEM计算方法及制导指令,拦截弹最终进入15 km末制导时,剩余ZEM仅不足30 m。根据拦截弹与目标飞行器相对速度,可以估算当目标不做进一步躲避机动时,拦截弹所需横向过载不足2g,能够满足实战中拦截要求。

5结论

①本文根据拦截临近空间飞行器的具体特点,简化目标飞行器模型以及拦截弹模型,给出了一种适用于拦截临近空间飞行器的零控脱靶量(ZEM)解析计算方法。

②仿真计算中,使用精确动力学模型的数值积分结果作为参照,验证了本文所提出方法的可行性。另外使用一种简化的预测方法,与本文提出方法进行比较,说明了本文提出的ZEM预测方法具有更高的预报精度。最后使用一种简单的中制导律,仿真验证说明本文方法更适用于拦截临近空间飞行器。

参考文献

[1]SONGEun-jung.Three-dimensionalmidcourseguidanceusingneuralnetworksforinterceptionofballistictargets.IEEETransactionsonAerospaceandElectronicSystems,2002,38(2):404-414.

[2]HULLDG.Missilesizingforascent-phaseintercept.JournalofSpacecraftandRockets,1995,32(3):445-449.

[3]SHINARJ.Nonorthodoxguidancelawdevelopmentapproachforinterceptingmaneuveringtargets.JournalofGuidance,Control,andDynamics,2002,25(4):658-666.

[4]YEHFK.Designofoptimalmidcourseguidancesliding-modecontrolformissileswithTVC.IEEETransactionsonAerospaceandElectronicSystems,2003,39(3):824-837.

[5]SHTESSELYB.Smoothsecond-orderslidingmodes:missileguidanceapplication.Automatica,2007,43(8):1 470-1 476.

[6]NEWMANB.Spacecraftinterceptguidanceusingzeroeffortmisssteering.AIAA93-3890.1993.

[7]NEWMANB.Robustconventionalbasedmidcourseguidanceforspacecragtintercept//TheAmaricanControlConfence.Seattle,Washington:AmericanSocietyforCybernetics,1995:1 123-1 125.

[8]NEWMANB.Strategicinterceptmidcourseguidanceusingmodifiedzeroeffortmisssteering.JournalofGuidance,Control,andDynamics,1996,19(1):107-112.

[9]刘世勇,吴瑞林,周伯昭.大气层外拦截弹中段制导研究.宇航学报,2005,26(2):156-163.

LIUShi-yong,WURui-lin,ZHOUBo-zhao.Researchonmidcourseguidanceforfue-exhaustion-shutoffexo-atmosphericinterceptor.JournalofAstronautics,2005,26(2):156-163.(inChinese)

[10] 郑立伟,荆武兴,张建英.适用于大距离拦截问题的零控脱靶量计算方法.宇航学报,2007,28(4):865-869.

ZHENGLi-wei,JINGWu-xing,ZHANGJian-ying.Zeroeffortmissformulationforlongerrangetargeting.JournalofAstronautics,2007,28(4):865-869.(inChinese)

[11] 陈峰,肖业伦,陈万春.基于零控脱靶量的大气层外超远程拦截制导.航空学报,2009,30(9):1 583-1 589.

CHENFeng,XIAOYa-lun,CHENWan-chun.Guidancebasedonzeroeffortmissforsuper-rangeexoatmosphericintercept.ActaAeronauticaetAstronauticaSinica,2009,30(9):1 583-1 589.(inChinese)

[12] 李运迁,齐乃明.基于零控脱靶量的大气层内拦截弹制导律.宇航学报,2010,31(7):1 768-1 774.

LIYun-qian,QINai-ming.Azero-effortmissdistance-basedguidancelawforendoatmoshpericinterceptor.JournalofAstronautics,2010,31(7):1 768-1 774.(inChinese)

[13] 郑立伟,荆武兴.大气层外拦截器近最优中制导律设计.宇航学报,2008,29(1):229-235.

ZHENGLi-wei,JINGWu-xing.Designofanearoptimalmidcourseguidancelawforexoatmosphericinterceptor.JournalofAstronautics,2008,29(1):229-235.(inChinese)

[14]O’NeillMaryKaeLockwood.Designtradeoffsonscramjetengineintegratedhypersonicwaveridervehicles.JournalofAircraft,1993,30(6):943-952.

[15]WEEKSDJ.SmallsatellitesandtheDARPA/airforceFALCONprogram//55thInternationalAstronauticalCongress.Paris:InternationalAstronauticalFederation,2004:3 565-3 574.