基于GARCH模型族的上证综指VaR计算

刘小冬，陈　俊，杜　欢

(西安财经学院， 陕西 西安　710100)

基于GARCH模型族的上证综指VaR计算

刘小冬，陈俊，杜欢

(西安财经学院， 陕西 西安710100)

摘要：VaR已成为近年来国际广泛应用的风险度量方法。文章选取我国2008年至2012年每个交易日。上证综指的收盘价，结合GARCH模型族，在正态分布、t分布、GED分布三种收益率序列分布假设下，对VaR的值进行了分析和对比，并应用Kupiec提出的“失败频率检验法”进行了准确性检验，通过实证分析得出，采用TGARCH—GED模型能够较好地反映股市风险。

关键词：上证综指 ；VaR方法；GARCH模型；准确性检验

一、文献综述

随着布雷顿森林体系的解体，从20世纪70 年代开始，全球金融持续动荡，而2008年金融危机和2009年欧债危机使得风险收益急剧变化，国际金融乃至世界经济受到巨大冲击。随着金融衍生产品的发展，风险的度量与管理已成为金融活动的中心。传统的通过方差、久期和CAPM等风险管理方法无法系统考虑金融市场中的各种风险，而VaR克服传统方法的缺陷，将风险数值化并逐渐在金融机构中推广应用。如今，VaR的重要性逐渐得以体现，也受到越来越多国内外学者的关注。

1993年G30集团《衍生产品的实践和规则》的报告，基于金融衍生产品首次提出了度量市场风险的VaR。Philippe[1]作为最早研究的学者之一，详细地介绍了如何使用VaR进行风险预算和风险管理。在我国，最先将VaR方法引入的是郑文通[2]，他分别概括了不同资产收益分布下VaR的计算方法，并介绍了VaR方法的用途和引入我国的必要性。王春峰[3]系统完整地讲解了VaR 的相关理论基础。姚刚[4]介绍了资产组合的VaR值的计算方法，并使用Black-Scholes 模型从线性和非线性范畴对VaR方法进行了说明。

GARCH模型是描绘波动率的模型，随着研究的不断深入，GARCH模型还作为一种分析算法被引入VaR的度量中。在股票市场风险研究中，Timotheos Angelidis、Alexandros Benos、Stavros Degiannakis[5]选取了五个股票指数计算投资组合日VaR的值，得出GARCH模型族的精确度对每一个投资组合是不同的。Andrea Beltratti、Claudio Morana[6]和Giot、Laurent[7]则采用GARCH模型族实证分析了单个股票指数的风险价值。邹建军、张宗益、秦拯[8]分别采用GARCH( 1, 1) 模型、RiskMetrics 和移动平均法计算上海股票市场的VaR 值，并通过返回检验得出GARCH( 1, 1) 能较好地反映上海股市的风险。闫志刚[9]基于GARCH族模型探讨了我国上证指数的波动性，研究发现选择的模型中EGARCH模型的拟合度最好，而GARCH-M模型在上海股票市场不适用。

然而，传统的VaR估计方法不考虑金融时间序列尖峰厚尾和波动聚集性的特点，假定收益率序列服从假设条件过于严格的正态分布，从而导致风险的估计会出现较大的误差。因此，为更好描述金融时间序列的特征，越来越多的学者开始关注资产序列的概率分布。Lee、Sue、Liu[10]和Cheng、Hung[11]，分别引入偏态广义误差分布(SGED)实证分析标准普尔500指数、道琼斯指数，引入偏态广义t分布(SGT)分析能源和贵金属市场的风险价值，得出基于SGED分布和t分布的模型计算的VaR值优于传统的 GARCH-N模型。林美艳、薛红刚[12]对上证综合指数采用GARCH( 1, 1)模型，并在收益率分别从正态分布和t分布的假设前提下考虑静态和动态VaR的计算方法,实证得出模型GARCH-t4 .869是最优的。陈守东、俞世典[13]对深圳股票市场和上海股票市场分别建立GARCH-N模型、GARCH-GED模型、GARCH-t模型估计风险价值，分析得出正态分布不能够很好地反映收益率的特征以及深圳股票市场面临的风险较大。

本文在国内外学者的研究基础上选取最近6年上证综指数据，基于GARCH模型、GARCH-M模型、TGARCH模型、EGARCH模型，选取不同的置信区间并扩充其扰动项的条件分布，分别假设服从正态分布、t分布和广义误差分布(GED)下计算我国上证综指的风险价值，并检验模型的准确性。

二、GARCH模型族

GARCH模型一般通过条件均值方程和条件方差方程来预测收益率序列的波动性和相关性。条件均值方程通常采用简单的形式，如，rt=μ+εt，其中μ为无条件均值，εt为扰动项。GARCH模型更关注展现不同模型之间差异的条件方差方程，在正态分布不能充分描述时间序列数据特性的情况下，GARCH模型假定εt服从t分布或一般误差分布。对GARCH模型进行深入研究后，学者们又逐步发展了非对称GARCH模型、指数GARCH模型和因子GARCH模型等，并广泛地应用于金融机构的风险度量研究。下面简介各类GARCH 模型。

(一)GARCH模型

GARCH(p,q)模型的主要思想是：条件方差方程中滞后期的误差项εt-i(ARCH项)和滞后期的条件方差σt-j(GARCH项)均是当期条件方差的影响因素。数学形式如下：

(ω>0,α1,…，αi，…,αq≥0;β1,…，βj，…,βp≥0)

(1)

其中，α是回报系数，β是滞后系数。

(二)GARCH-M模型

1987年Engle、Lilien 和Robins[14]在GARCH模型的均值方程中引入条件方差，提出了GARCH-M模型，即资产收益率序列也会受到自身方差的影响，来解释说明资产的期望收益与期望风险相关，期望风险系数的估计值可视为风险—收益的抵换系数(risk-return tradeoff)。

条件均值方程：

(2)

条件方差方程：

(ω>0,α1,…，αi，…,αq≥0;β1,…，βj，…,βp≥0)

(3)

然而GARCH模型在应用中仍具有一定的局限性：第一，以上模型要求系数的值均非负，在一定程度上制约了条件方差的动态性；第二，GARCH模型属于对称模型，条件方差仅与εt-i项的幅度相关，与符号无关。这与实际相悖，实际的金融价格运动受到正负消息的影响是不对称的，即存在杠杆效应( leverage effect )。为表明正负两类残值不对称的反馈现象，在上述模型的基础上发展了EGARCH模型、TGARCH模型等非对称GARCH模型。

(三)TGARCH模型

Glosten、Jaganathan 和Runkle[15]提出门限GARCH模型(Thresholed ARCH，简称TGARCH模型)，在条件方差方程中引入虚拟变量考虑正负误差项对条件波动的不同影响。

其数学表达式为：

(4)

其中Dt-i是虚拟变量，当εt-i<0时，Dt-i=1；否则，Dt-i=0。

(四)EGARCH模型

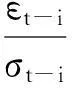
EGARCH(p,q)的模型指定条件方差为：

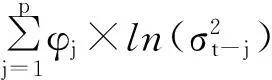
(5)

三、实证分析

(一)数据的选取和处理

在本文中，所选取的数据为2008年1月2日至2012年12月31日每个交易日上证综指的收盘价，共1 457个观测值。数据来源于大智慧软件。分析采用的软件是EVIEWS7.2和EXCEL2007。设第t天的上证综指的收盘价为pt，为了消除误差，对收益率同时采用对数形式：

(6)

(二)数据的统计特征分析

图1　上证综指日收益率序列

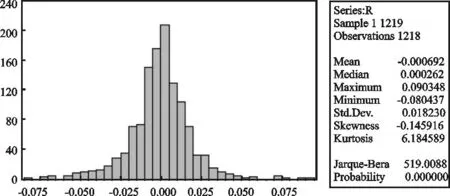
图2　上证综指日收益率分布直方图

如图1所示，日收益率序列波动呈现出明显的时变性、突发性和群聚效应。图2上证指数收益率偏度-0.145 916，左偏峰度6.184 589(正态分布偏度为0，峰度为3)，可以看出日收益率呈左偏、尖峰厚尾形态，且JB 统计量为 519.008 8，其正态性检验也证实了收益率r偏离正态分布。

(三)模型检验

1.平稳性检验

收益率数据平稳性检验采用的是单位根 ADF 检验，其中根据 SIC 信息准则，使其值最小滞后阶数为最优，通过分析选择滞后1期，且r均值几乎为零，选择无截距检验，ADF 统计量检验的p值非常小，所以断定此序列是一个平稳序列(见表1)。

表1ADF检验结果

2.自相关检验

通过检验可知，各阶滞后的Q 统计量的p值都大于0.05，且由相关系数AC 和偏相关系数PAC可以看出在95%的显著水平下，残差序列不存在序列自相关。

残差序列的平方存在高阶自相关，各阶滞后的Q 统计量的p值都小于0.05。

3.ARCH效应检验

Engle提出LM检验法，来检验收益率序列是否能够建立ARCH模型。如表2所示：当q=3 时， LM统计量的χ2检验和F统计量的P值均为0.000 0，即收益率的残差序列高阶ARCH 效应明显，符合GARCH模型建立条件。

表2ARCH-LM检验结果

(四)模型的建立及预测

本文采用样本内预测，对2008-2013年上证综指的日收益率分别建立了GARCH、GARCH-M、TGARCH、EGARCH 模型进行比较。对于每个模型本节都选取2013年的数据为对照组，首先通过2008 -2012 年的前1 218个数据来估计模型的参数，然后再预测2013 年238个交易日的上证综指收益率的日VaR值，最后将预测的值进行事后检验。估计的结果如表3-6所示。

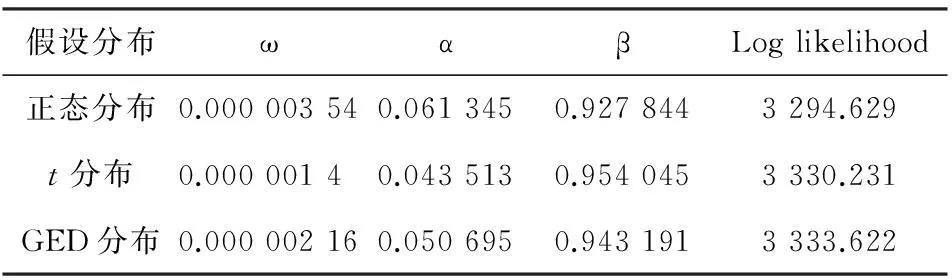
表3　GARCH(1,1)模型的参数估计结果

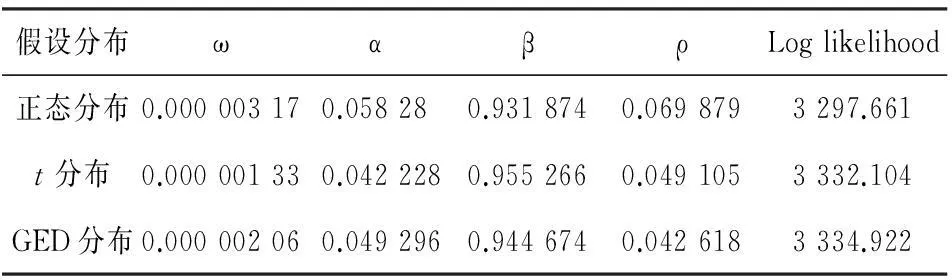
表4　GARCH(1,1)-M模型的参数估计结果

表5　TGARCH(1,1)模型的参数估计结果

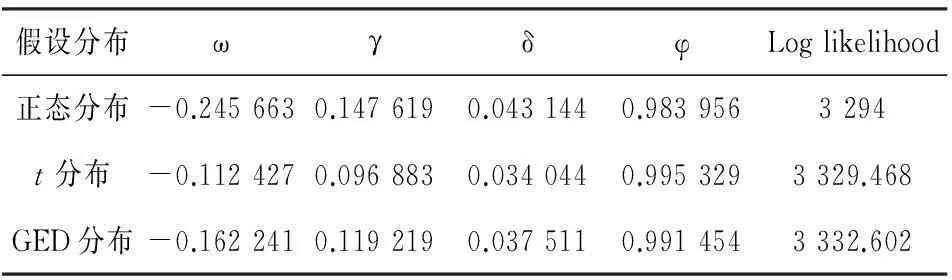
表6　EGARCH(1,1)模型的参数估计结果

表7　2013年VaR估计结果的事后检验

(五)基于失败率的VaR检测

本文对 VaR模型进行事后准确性检验选用Kupiec[17]提出的“失败频率检验法”。Kupiec假设VaR估计具有时间独立性，将准确性检验转化为检验失败率的零假设。在置信水平为c下失败的期望概率p*=1-c，那么失败检验的二项式结果即为一系列独立的伯努利实验。

假定失败率为p=N/T(T为样本数，N为失败次数)，Kupiec提出了对零假设p=p*的似然比率检验：

(7)

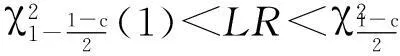
本文用于检测的样本共238个，按照该方法，置信水平95%和99%的非拒绝域分别为5

四、结论

金融风险管理的VaR方法是近几年来学术界关注的重点。我国研究分析的一个重要目的就是要科学有效地管理市场风险，提高资金的利用率。本文基于GARCH模型族，充分结合残差项服从正态分布、t分布、GED分布的三种假设，在不同的置信水平下量化分析我国上证综指的VaR，并对模型有效性进行检验。得出如下主要结论：

第一，根据日收益率序列的统计特征可以分析得出传统的VaR计算方法并不能够反映上证综指尖峰厚尾和波动集聚的特点，本文通过实证分析得出GARCH模型族能够较好地描绘金融时间序列的短期波动。在建立的GARCH模型族中，TGARCH模型和EGARCH模型都能够很好地解释股票市场对非对称冲击的反馈信息，且TGARCH模型计算的结果更符合实际。

第二，从参数ρ(见表4)可以看出，收益率序列自身的波动对收益有较小的影响，说明上海股票市场并不适用GARCH-M模型。同时参数τ(见表5)为负和参数δ(见表6)为正，条件方差在同等条件下，利好消息比利空消息更为敏感，说明存在杠杆效应，反映了我国股票市场的信息不对称以及“政策市”的存在。目前这种政府定位以及不成熟的市场环境使市场机制不能充分发挥，我国证券市场缺乏卖空机制。

第三，在VaR 值的测算方面，分别在99%和95%置信水平下进行了准确性检验，得出在95%置信水平下，几乎所有模型计算的VaR值过于保守，而基于GED 分布的模型VaR值被高估可能性被降低，且其计算的精准度也比t分布模型高。VaR值被高估在一定程度上会造成资金流动率过低，财务杠杆未能充分利用，致使企业竞争力不足。总的来说，采用99%置信水平下基于TGARCH-GED模型能够更好地反映上海股票市场风险。

参考文献

[1]PHILIPPE JORION.Risk:measuring the risk in Value-at-Risk[J].Financial Analysis journal,1996(11):47-56.

[2]郑文通.金融风险管理的VaR 方法及其应用[J].国际金融研究,1997(9):59-62.

[3]王春峰,万海辉. 金融市场风险测量模型- VaR[J] . 系统工程学报,2000 ,15 (1) :67-75.

[4]姚刚.风险值测定法浅析[J].经济科学,1998(1):55-60.

[5]TIMOTHEOS ANGELIDIS， ALEXANDROS BENOS， STAVROS DEGIANNAKIS. The use of GARCH models in VaR estimation[J]. Statistical Methodology,2004,2(1):105-128.

[6]ANDREA BELTRATTI,CLAUDIO MORANA.Computing value at risk with high frequency data[J].Journal of Empirical Finance,1999(6):431-455.

[7]GIOT P,LAURENT S. Modeling daily value-at-risk using realized volatility and ARCH type models [J].Journal of Empirical Finance, 2004(11): 379-398.

[8]邹建军,张宗益,秦拯.GARCH模型在计算我国股市风险价值中的应用研究[J].系统工程理论与实践,2003(1):22-25.

[9]闫志刚.上海证券市场GARCH效应检验和模型选择[J].统计与信息论坛,2005(1):66-69.

[10]MING CHIH LEE,JUNG BIN SU,HUNG CHUN LIU.Value-at-risk in US stock indices with skewed generalized error distribution[J].Applied Financial Economics Letters, 2008(4):425-431 .

[11]WAN HSIU CHENG,JUI CHENG HUNG.Skewness and leptokurtosis in GARCH-typed VaR estimation of petroleum and metal asset returns[J].Journal of Empirical Finance, 2011(18):160-173.

[12]林美艳,薛宏刚.VaR模型及其在上海股市中的应用[J].辽宁大学学报,2006,33(1):6-10.

[13]陈守东,俞世典.基于GARCH 模型的VaR方法对中国股市的分析[J].吉林大学社会科学学报，2002(4):11-17.

[14]ENGLE R F,LILIEN D M,ROBINS R P.Estimating time Varying Risk Premia in the term structure : the ARCH-M Model [J].Econometrica,1987,55(2):391-407.

[15]GLOSTEN L R,JAGANATHAN R，RUNKLE D.On the relation between the expected value and volatility of the nominal excess return on stocks[J].Journal of Finance,1993(48): 1779-1801.

[16]NELEON,DANIEL B. Conditional heterosdasticity in asset Returns :a new approach[J].Econometrica,1991(59):347-370.

[17]KUPIEC P H. Techniques for verifying the accuracy of risk measurement models[J].The Journal of Derivatives, 1995(2):73- 84.

(责任编辑：任红梅)

收稿日期：2014-10-14

基金项目：陕西省自然科学基金项目(2014JM93067)

作者简介：刘小冬(1963-)，男，陕西西安人，西安财经学院管理学院教授，博士，硕士生导师，研究方向为博弈论及其应用；陈俊(1990-)，女，陕西安康人，西安财经学院硕士研究生，研究方向为金融工程；杜欢(1988-)，女，陕西西安人，西安财经学院硕士研究生，研究方向为金融工程。

中图分类号：F830.91：F224

文献标识码：A

文章编号：1672-2817(2015)02-0023-05

Research on Calculation of VaR of Shanghai Composite Index
Based on GARCH Family Models

LIUXiao-dong,CHENJun,DUHuan

(Xi’an University of Finance and Economics,Xi’an 710100,China)

Abstract:VaR methods have become a global consensus measurement of risk in recent years . On the basis of theoretical analysis of VaR, this article takes the Shanghai composite index in our country as an example, combining with GARCH family models, analyses and compares the consequence of VaR under the assumptions of the normal distribution,t distribution and GED distribution. Besides, it uses the Kupiec method to verify the accuracy. Through the empirical analysis, it is concluded that the TGARCH-GED model can better reflect the risk of stock market.

Keywords:Shanghai composite index; VaR methods; GARCH models; accuracy test