小型食品粉碎机的双层隔振系统优化设计
2015-12-31朱秀琳李成清翁秀奇
朱秀琳 李成清 翁秀奇
(南京工业职业技术学院,江苏 南京 210023)
小型食品粉碎机目前在中国使用非常普遍,给人们生活带来诸多便利。尽管生产企业一直致力于产品功能完善,但是其振动与噪声问题一直得到有根本解决。目前未发现有针对此类产品噪声问题的研究见诸于文献。
本设计以某款小型食品粉碎机(图1)为研究对象,该机最高工作转速为30 000r/min,正常工作时噪声达到66dB,超过GB 3096—2008《声环境质量标准》规定的“居民住宅小区区域环境噪声平均等效声级须达到环境质量1类标准,即昼间55dB,夜间45dB”。
该机由杯体1(盛食物、刀具由刀杆与机身内连接)、机身3(内装有电机、轴承、电脑板等)组成。粉碎作业时,在电机高速旋转下,电机、轴承、刀片、机身、杯体及被粉碎食品会出现振动,并产生噪声。杯体与机身合缝处以及机身底部均有4只沿圆周均布的橡胶隔振垫,共同组成双层隔振系统。本设计拟基于MATLAB编程与图形功能,对隔振系统进行优化。

图1 小型食品粉碎机Figure 1 A smal pulverizer
1 数学模型的建立
相对来说,杯体、机身比隔振垫的刚度大很多,故将杯体、机身简化作刚体,质量分别为m1、m2,因塑料把手中空质量较轻忽略,故m1、m2的质心均在其圆柱中心线上。第1层3只隔振垫x向总刚度为K1、粘性阻尼系数为C1,第2层4只隔振垫x向总刚度为K2,粘性阻尼系数为C2。激励力F(t)可以看做简谐力,F(t)=F0sinωt,传入基础的力为FT(t),x1、x2为绝对位移,其数学模型见图2。
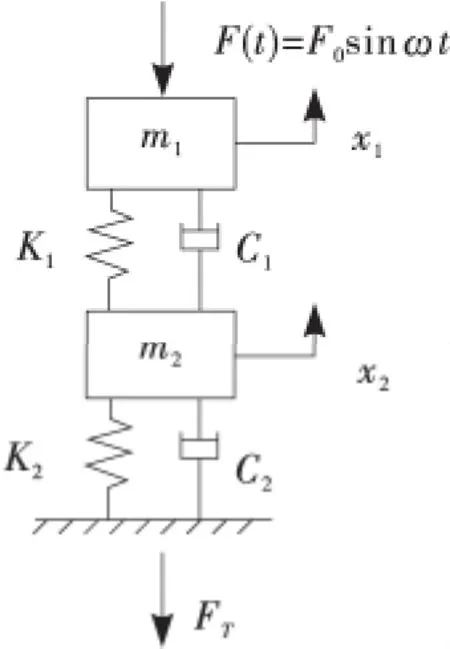
图2 数学模型Figure 2 Mathematical model
根据牛顿第二定律,系统运动微分方程为[1]:

令FT(t)=H(ω)F(t),解微分方程(1)可以得到系统频响函数[1]:

其中,Δ=(K1-m1ω2+jC1ω)[K1+K2-m2ω2+jω(C1+C2)]-(K1+jC1ω)2。

由式(2)整理得到用无因次量表示的频响函数:

其中,A=λ4-λ2(α2+4ζ1ζ2α+μ+1)+α2;C=α2-4ζ1ζ2αλ2;B=2λ3(ζ2α+ζ1μ+ζ1)-2λα(ζ1α+ζ2);D=2λα(ζ1α+ζ2)。
因此,双层隔振系统的绝对传递率:

2 动态特性分析
单层隔振系统只要合理选择刚度比、阻尼比参数,在低频区(<50Hz)能起到很好的隔振效果。但是对高频干扰(>100Hz)的隔振效果并不理想,并且隔振的频段也比较窄[1-6],而大部分结构噪声都是高频的。因此,双层隔振应运而生,越过共振区后双层隔振的传递率斜率从单层的12dB/oct增加到24dB/oct[1-6],这对于高频振动的隔离意义重大。
影响双层隔振系统隔振性能的参数主要有质量比、阻尼比、固有频率比。以频率比λ为横坐标、以隔振系统绝对传递率TA为纵坐标,分别以质量比、阻尼比、固有频率比为参变量,基于MATLAB编程与图形功能,由式(4)研究参变量变化时绝对传递率TA的变化规律。为了使图形表达清晰,横坐标取对数lgλ,纵坐标取振动级差变化的分贝数,即20lg|H(λ)|。
由图3可知,随着质量比μ的增大,振动传递率曲线的第1峰位置左移而第2峰位置右移,故隔振频带变宽,隔振效果变好,尤其在第1峰与第2峰之间效果最好。例如当ζ1=0.03,ζ2=0.05,α=1.2,λ=1,μ从1增加到4时,振动级差减小了12dB。但是在高频区即第2峰后,质量比的变化对隔振效果影响不大。
由图4可知,固有频率比α的变化对隔振效果影响非常显著,且分布在整个低频及高频区。随着α的变大,隔振效果变差。例如当ζ1=0.03,ζ20.05,μ=1.538,α从1.4减少到0.5,λ=1和λ=10时,振动级差分别减小了17.96,18.75dB。
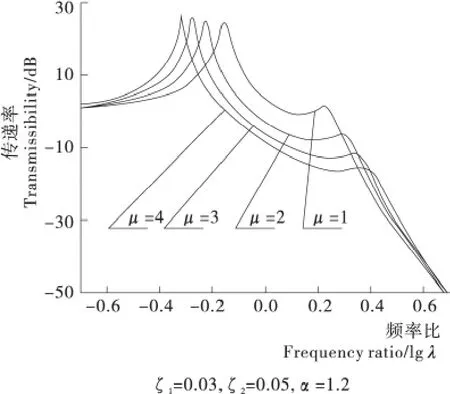
图3 质量比变化对隔振效果的影响Figure 3 Magnification factors of vibrations at different mass ratio
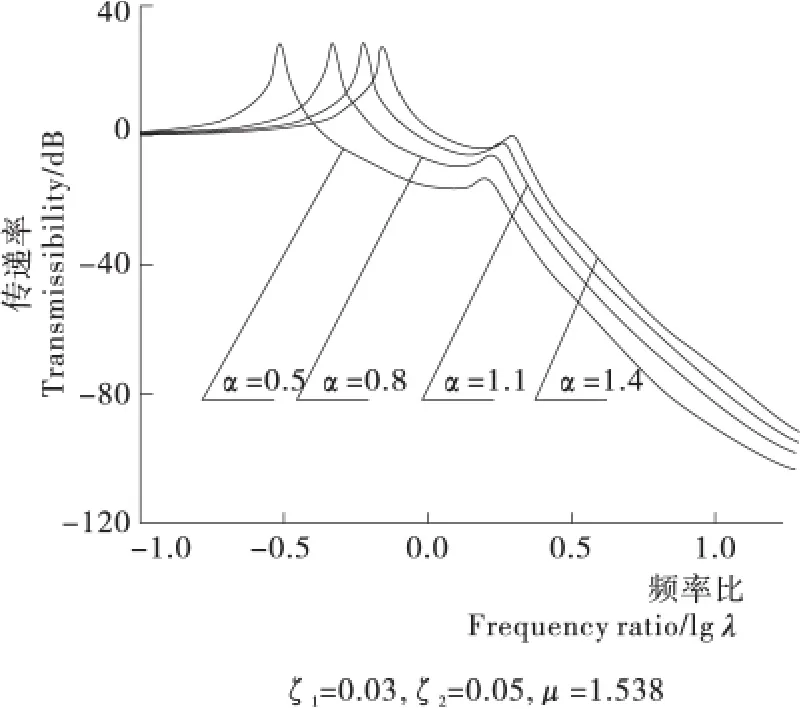
图4 固有频率比变化时对隔振效果的影响Figure 4 Magnification factors of vibrations at different natural frequency ratio
由图5(a)可知,阻尼比ζ1变化时(取ζ1=0.02~0.15,ζ2=0.02,α=1.5,μ=1.538),在低频区仅仅在共振区域随着ζ1增大能明显减小振动级差,而其他区域几乎无影响。但是在高频区(λ>2.5)时,ζ1增大反而会降低隔振效果。例如当λ=10,ζ1由0.02增加到0.15时,振动级差增加了9.7dB。
由图5(b)可知,阻尼比ζ2变化时(取ζ2=0.02~0.15,ζ1=0.02,α=1.5,μ=1.538),在低频区对隔振效果的影响与ζ1的相同,只是区域变宽(λ由2.5扩大到10)。在高频区λ>10,传递率曲线发生逆转,即随着ζ2的增大,反而会降低隔振效果。例如当λ=33,ζ2由0.02增加到0.15时,振动级差增加了15.33dB。
3 优化设计
利用频谱与相干分析法测试如图1所示的小型食品粉碎机,其振动和噪声频率集中在368Hz,倍频为744,1 104,1 472,2 216,2 584Hz,均属于高频振动范围,因此,采用双层隔振尤为必要。该机器也是如此设计的,但是噪声指标仍然不达标。本设计拟利用MATLAB编程,采用单纯形优化算法[7],优化隔振系统从而达到减振降噪目的。

图5 阻尼比变化对隔振效果的影响Figure 5 Magnification factors of vibrations at different damping ratio
3.1 目标函数
根据以上双层隔振系统动态特性分析,在高频区为增加隔振效果,应该尽量增加质量比μ、取较小的阻尼比ζ1和ζ2以及尽量减小固有频率比α。但是,有些参数的改变是受限的。例如,增加质量比,如果增加机头质量,则增加了整机重量,使小型家电变得笨重。如果减小机身重量,则要减少本来就很小巧的各种电子元器件质量。况且,在高频区质量比的变化对隔振效果影响程度不大,所以,本机质量比(μ=1.452)不做修改。
因此,本机双层隔振系统参数优化主要从适当调整阻尼比、优化固有频率比(选择合适隔振垫固有频率)的角度出发。
本设计以减小双层隔振系统振动级差为目标。

3.2 约束条件
橡胶隔振垫的种类很多,其性能主要取决于橡胶配方、隔振垫形状以及硫化工艺。目前中国标准化的橡胶隔振垫主要有XD型和WJ型[8,9],也可根据隔振性能要求自行设计。橡胶的阻尼比较大,ζ可达0.15,但是常用范围在0.02~0.08。橡胶垫的固有频率范围一般在10~20Hz[8,9]。即:

3.3 优化计算
采用无约束最优化直接算法:单纯形法。此算法不用求导,虽然收敛较慢,但是编程简单,由于本优化函数变量不多,也能收到较好效果。
经过测试,该机器各项动态特性原始参数为:机头m1=1.35kg(包含常规预估食物重量),机身m2=0.93kg,ω1=10Hz,ω2=15Hz,ζ1=0.10,ζ2=0.07。输入原始数据及约束条件,优化计算后结果见表1。可见,只要调整阻尼比ζ1、固有频率ω2至表1中数值,本粉碎机的隔振系统在工作噪声频率区域的振动级差就会降低10~13dB。
3.4 系统改进
根据优化结果,重新选取新的隔振垫:即ζ1=0.03,ω2=10.5Hz,其它参数不变。按照相同步骤再次测试该机工作噪声为53.9dB,已符合GB 3096—2008《声环境质量标准》的规定。

表1 粉碎机工作噪声区域振动级差计算Table 1 Calculation of Magnification factors of vibrations on the noise area of the pulverizer dB
4 结论
基于MATLAB的编程、图形与计算功能,分析了双层隔振系统的各项动态参数对隔振性能的影响,在此基础上利用单纯形优化算法对该食品粉碎机的双层隔振系统的参数进行了优化计算,然后根据优化结果重新选取隔振垫,经测试噪声指标降低了12.1dB,解决了该机器工作噪声超标的问题。
1 严济宽.机械振动隔离技术[M].上海:上海科学技术出版社,1985:21~93.
2 刘迎春,王开和.基于弹性体模型的双层隔振器结构参数设计[J].天津科技大学学报,2006,21(3):57~19.
3 孙京平,王开和,卢学军,等.水泵的双层隔振设计[J].机械设计与制造,2006(3):5~7.
4 Cai Liang-bin,Chen Da-yue.A two-stage vibration isolation system featuring an electrorheological damper via the semiactive static output feedback variable structure control method[J].Jounal of Vibration and Control,2004,10(5):683~706.
5 苏荣华,彭晨宇,丁文文.设计参数对双层隔振系统动态性能影响的研究[J].应用基础与工程科学学报,2008,16(6):863~869.
6 骆江峰.降低往复式压缩机振动与噪声的设计[J].食品与机械,2006,22(6):91~94.
7 陈宝林.最优化理论与算法[M].北京:清华大学出版社,2005:341~369.
8 周新祥.噪声控制技术及其新进展[M].北京:冶金工业出版社,2007:152~160.
9 张弛.噪声污染控制技术[M].北京:中国环境科学出版社,2007:186~206.
