基于三种模型的昆士兰州短期电力负荷预测对比探究

智 勇,何 欣,梁 琛,刘 巍

（国网甘肃省电力公司电力科学研究院，甘肃兰州，730050）

0 引言

电力系统的主要任务是向用电单位提供安全、可靠和稳定的电能，满足用电单位的用电需求。电力负荷指电力的需求量或者用电量，在本文的研究中的电力负荷是指在某时点电力市场上电能交易的成交量电量。与其他产品不同，电能难以储存，具有即产即用的特点，电力市场的供需平衡，即电能的产出量与消耗量平衡对于电力系统的稳定非常重要，也是电力系统正常运行的首要条件。提高电力负荷预测精度，对于合理调整电网内部的发电机组的开停，保证各用电单位的电力需求用重要意义，同时准确的电力负荷预测可以减少资源浪费，从而提高社会经济效益。因此电力负荷预测愈来愈受到重视，并且它也是现代电力系统能量管理的重要部分。

电力负荷从预测周期上分，可以分为长期、中期、短期以及超短期预测，本文预测周期长度为半小时，周期介于短期与超短期之间。从电力负荷预测方法来划分，可以划分为传统预测方法、现代预测方法和组合预测方法，其中传统预测方法包括回归分析法、时间序列法、Kalman 滤波等，现代预测方法主要包括人工神经网络，支持向量机，小波分析等，组合预测法的思想是将多个模型组合起来以发挥各自模型的优势，弥补单个模型的不足，以提高模型的预测精度的一种方法。每种方法都有个各自的优点，没有一种方法绝对准确，也没有一种可以适用于所有电力系统的方法，需要根据特定的情况选择不同的预测方法。

与组合方法思想相似，近年许多学者提出了多种将不同预测方法混合的预测方法，由于混合方法能发挥多种预测方法的优势，进而能提高模型的预测精度。为提高电力负荷预测模型的预测精度，本文将基础ARMA 模型与Kalman 滤波结合建立ARMAKalman 滤波模型，将ARMA 模型与SVM 模型以及SVM 的优化方法结合，建立ARMA-SVM 模型，并将上述三种模型（包括基础ARMA 模型）应用于澳大利亚昆士兰州的电力负荷预测中，进而对比了三个模型的预测效果。

1 方法描述

本文以ARMA 时间序列分析模型作为拟合和预测的基础模型，并将其与Kalman 滤波和SVM（Support Vector Machine）分别结合成ARMA-Kalman 模型和ARMA-SVM 模型以预期提高模型的预测精度。其中，ARMA-SVM 模型中的SVM 部分的参数对模型的准确性、拟合精度和预测精度都有很大影响，选择合适的模型参数对建立合适的模型很重要，在本文中利用遍历的方法来确定模型中SVM 部分的参数。文章中用到的三种模型介绍如下。

1.1 ARMA 模型

ARMA 模型是一种经典的被广泛应用于时间序列分析模型，最早由Box 和Jenkins 提出，其根据序列的自相关系数和偏自相关系数确定模型的阶数，模型表达式如下：

其中：φ( B ) = 1-φ0B0-φ1B - … -φpBp；θ( B ) = 1 -θ1B - … -θqBq，xt表示t 时刻的观测值，B 为延迟算子（注：此处定义 B0xt= 1），偏自回归项的系数。at表示模型在t 时刻的误差值。根据延迟算表示模型的自回归项的系数，模型的子的含义，模型可以展开成如下形式：

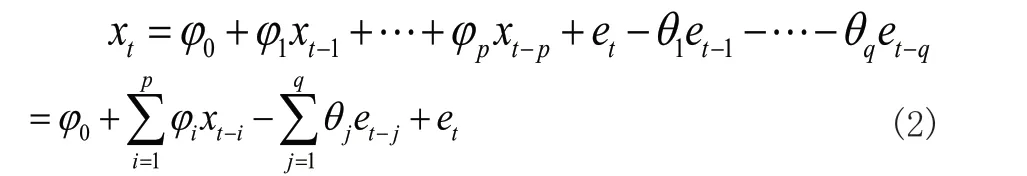
1.2 Kalman 滤波

Kalman 滤波一般由量测方程和状态方程组成，根据误差协方差最小的准则推导出Kalman 的递推滤波公式，具体推导过程在这里不作详细描述，可以参见文献[2]。

陆如华，何于班(1994)将Kalman 滤波应用于线性回归中，并推导出了线性回归方程下的Kalman 滤波的递推关系式。在线性回归方程条件下， Kalman 滤波状态方程(3)和量测方程(4)如下：

变量矩阵，Yt为t 时刻因变量向量，εt、υt分别为t 时刻回归系数

其中，βt为t 时刻回归方程的回归系数向量，Xt为t 时刻自误差向量和预测误差向量。

根据误差协方差最小的准则，推导出如下Kalman 滤波递推公式：

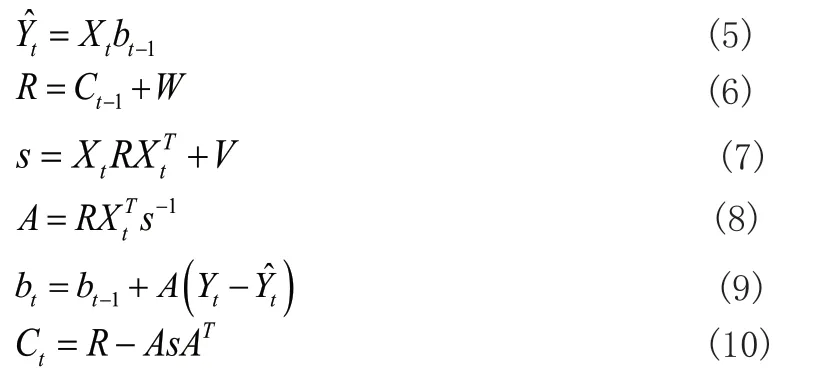
1.3 ARMA-Kalman 模型

本文中将ARMA 模型与Kalman 滤波结合建立ARMA-Kalman模型，该模型的流程图如图 1 所示。模型首先建立ARMA 方程，并以此作为Kalman 滤波的先验模型，根据所得的模型，确定Kalman 滤波的初始化参数。从算法流程图中可以看出，该模型与基于线性回归的Kalman 滤波的不同之处如下：

(1) 模型的被预测向量不同，在线性回归Kalman 滤波中，被预测向量中不包含因变量，而在ARMA-Kalman 模型中，被预测向量定义如下式(11)所示：

(2) 模型的因变量矩阵不同，ARMA-Kalman 模型中的因变量矩阵是根据所建立的ARMA 模型来确定的，定义如下下式(12)所示：

式(11)(12)中的T 为预测向量的使用预测点之前的期间长度，同时也是因变量矩阵的行数。引入T 是为了降低一步预测时，由单步误差带来的误差协方差阵的剧烈波动。

1.4 SVM 模型

SVM（Support Vector Machine）模 型 最 早 由Vapnik Vladimir (1995)正式提出，其理论基础（支持向量机理论）是从统计学习理论发展而来的，最初被应用于模式识别，经过短期发展，模型被应用于回归方面，并取得了良好表现。SVM 回归的基本思想是，通过将低维输入空间映射到高维空间，然后在高维空间中进行线性回归，从而得到原低维度非线性回归方程，本文选取 SVRε- 做回归。

SVM 所要建立的模型表达式如下：

其中w 为权值向量，b 为阈值，(· )为特征空间中的点积，φ( x)

为映射函数。ε - SVR按照如下目标确定参数w 和b ：

使得：

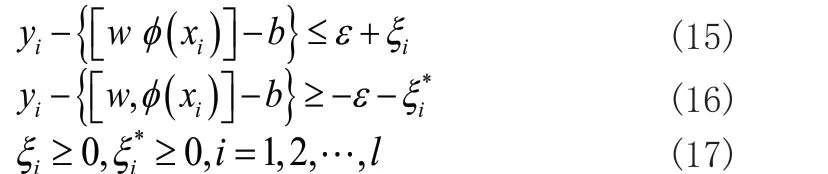
SVM 中的从低维空间向高维空间映射是通过核函数完成的，常用的核函数有d 阶多项式内积核函数、径向基内积核函数sigmoid 内积核函数，本文建立的 ε- SVR中选取径向基核函数。

径向基内积函数表达式如下：

在 SVRε- 模型中参数C 和σ 的选择，对模型的精度影响很大。在本文中，先设定参数C 和σ 的取值区间，然后将两个参数的取值区间等分，将C 和σ 的取值区间上的等分点两两组合作为C和σ 的估计值，带入到模型中，最终求出最优的C 和σ 值。

1.5 ARMA-SVM 模型

类似于ARMA-Kalman 模型，本文将从所建立的ARMA 模型提取出的如式(19)及式(20)所示的输入矩阵与输出向量用于构建SVM 模型，然后优化其参数C 和σ 。

其中N 为被拟合或者被预测的长度。

2 实例研究

本文选取澳大利亚昆士兰州2011 年11 月份每半小时电力负荷作为研究对象，建立以上所述的三种模型并对比他们的预测效果，在所有三个模型中均选取前21 天数据作为训练集建模拟合，后9 天数据作为测试集测试所建立模型的预测效果。模型的预测结果对比图如图 2 所示：

常用于衡量模型的预测精度的指标有平均百分比绝对误差（MAPE）、平均绝对误差（MAE）和均方误差（RMSE），指标的表达式如以下三式所示：

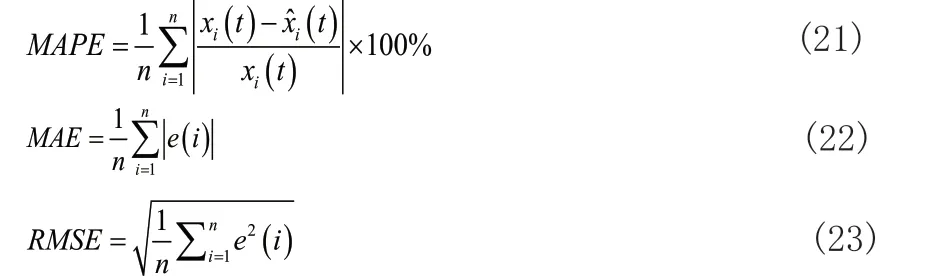
不同模型的预测精度如下表 1 所示：

从表 1 可以看出，三种模型的预测精度都很高，都达到了0.7%以内，其中ARMA 模型与ARMA-Kalman 模型的预测指标接近，ARMA-SVM 模型较前两者的预测精度更高。在基础ARMA 模型的预测精度已经很高的情况下，ARMA-Kalman 模型，ARMA-SVM 模型仍能相对提高模型的预测精度，一定程度上说明了模型在电力负荷预测中的性能良好。

3 结语

为提高电力负荷预测模型的预测精度本文将基本ARMA 模型与Kalman 滤波结合建立ARMA-Kalman 滤波模型，将ARMA 模型与SVM 模型以及SVM 的优化方法结合，建立ARMA-SVM 模型，以试图提高模型的预测精度。本文将前两个模型以及应用于澳大利亚昆士兰州的2011 年11 月份每半小时的电力负荷预测中，将其中前21 天的数据作为训练集用于建立预测模型，将剩下9 天的数据用来检验模型的预测效果。实例研究表明，在对ARMA-Kalman 模型未能如期较大提高对澳大利亚昆士兰州的电力负荷预测精度，ARMA-SVM 模型在一定程度上提高了预测精度。

[1] 马睿.超短期电力负荷预测的多模型极限学习算法 [硕士]: 上海交通大学； 2011.

[2] 黄巧玲.基于相空间重构与卡尔曼滤波计算组合的汇率时间序列预测 [硕士]: 华侨大学； 2007.

[3] 陆如华，何于班.卡尔曼滤波方法在天气预报中的应用[J].气象.1994(09):41-3+0.

[4] 关颖.支持向量机在电力系统短期负荷预测中的应用 [硕士]:天津大学； 2006.