长航时激光惯导定位误差的补偿方法研究

李莹

（解放军92941部队，125001）

0 引言

对于惯性导航系统而言，惯性敏感元件(包括陀螺仪和加速度计)的误差是影响惯性导航系统精度的主要决定因素。陀螺仪是敏感壳体相对于惯性空间角运动的装置，它的基本功能是敏感角位移和角速度。作为一种重要的惯性敏感器，它广泛用于测量运载体的运动，而且还是构成惯导系统的核心元件，惯导系统的定位精度很大程度上取决于陀螺仪的工作精度。无论何种应用还是何种形式的陀螺仪，陀螺漂移始终是制约其所使用系统的精度的关键问题。陀螺漂移误差一般分为常值漂移和随机漂移两部分，惯性器件常值误差可以进行有效地补偿，但是它会随着时间逐渐变化，而且在惯性导航系统每次启动时，常值漂移都会不一样。本文首先分析了陀螺漂移对非旋转惯导系统和单轴旋转激光惯导系统定位精度的影响，并进一步推导出惯性坐标系下的ψ（计算导航坐标系与计算机坐标系之间的矢量角）增量与陀螺漂移之间的关系。利用两次外部位置和航向信息对惯导的陀螺漂移进行补偿，从而达到对惯导定位精度的提高。

1 陀螺漂移对惯导定位误差影响的分析

1.1 陀螺漂移对非旋转惯导系统定位精度的影响

根据惯导的经典误差方程[1][2][3]，调用Matlab/Simulink子系统模块库中的Subsystem模块，建立仿真模型，针对陀螺漂移对位置误差的影响进行了静基座分析。

仿真条件假设为：在北纬40°的静基座上进行48h仿真，采样频率为1次/2s，共产生86400个仿真点。给定的误差源为：εx=0.01°/h或εy=0.01°/h或εz=0.01°/h或εx=εy=εz=0.01°/h；其它初值为0。仿真结果见图1。

图1（a） εx=0.01°/h、εy=0.01°/h、εz=0.01°/h 及εx=εy=εz=0.01°/h 时的经度误差δλ曲线

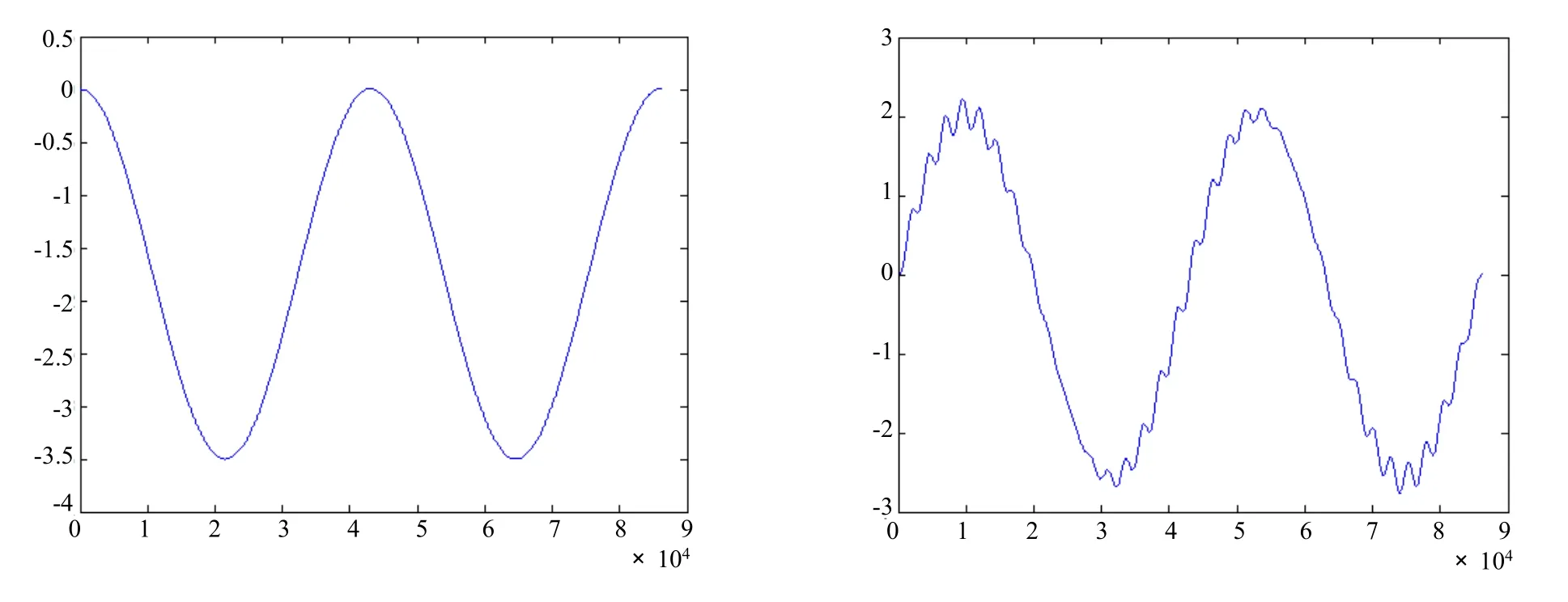
图1（b） εx=0.01°/h、εy=0.01°/h、εz=0.01°/h 及εx=εy=εz=0.01°/h 时的纬度误差δφ曲线

通过仿真及分析可以看出：东向陀螺漂移εx对经、纬度产生三种周期振荡误差，对经度产生正的常值分量，但它不引起随时间积累的误差；北向陀螺漂移εy对经、纬度产生三种周期振荡误差，对经度产生随时间积累的负的误差，对纬度产生正的常值误差；方位陀螺漂移εz对经、纬度产生三种周期振荡误差；对经度产生随时间积累的负的误差；对纬度产生负的常值误差。由于陀螺漂移引起的误差随时间增长的，对系统的精度具有决定性的意义，为了减小其影响，故在载体运动过程中，需要对陀螺漂移进行估算并施加补偿。

1.2 陀螺漂移对单轴旋转惯导系统定位精度的影响

传统的转子陀螺，其中的质量不平衡漂移与重力g是密切相关的，不恰当的设计会使系统旋转抵消陀螺常值漂移的同时又引入了与重力有关的漂移，所以传统转子陀螺应用于旋转调制技术时有其固有的弊端。但是光学陀螺较传统转子陀螺，因其全固态性、对重力g的不敏感性等，所以旋转不会造成光学陀螺本身精度的下降。所以自从激光陀螺出现以后，在旋转调制技术和捷联惯导系统的基础上出现了一种新型的惯导系统，即旋转调制式激光捷联惯导系统。

本文讨论的单轴旋转方法是令IMU以转速ω绕机体坐标系的竖直轴匀速转动。激光惯性导航系统的长时间定位精度，主要考虑经度发散误差，由文献4、文献5和文献6可知，长时间工作的激光惯性导航系统，其经度误差发散程度可按式（1）表示：

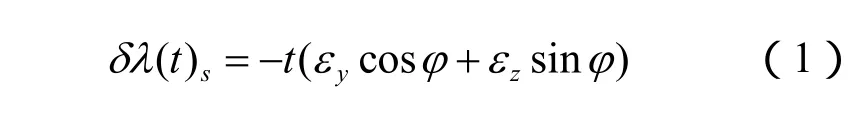
从式（1）可以看出，长时间工作的激光惯性导航系统，其定位精度主要受其北向和天向陀螺漂移影响，此外，还与其工作的地理位置有关。对于单轴旋转激光陀螺惯性导航系统而言，其北向激光陀螺漂移εx能受到最有效地调制，其对系统精度误差的影响可以基本消除，只剩下天向陀螺漂移εz对系统精度误差的影响。因此在舰船长时间航行时，只需要对激光惯导天向陀螺漂移εz进行补偿。

2 基于外部位置和航向信息校正方法

3 长航试验验证

针对激光惯导我们进行了航行状态下72h的试验验证。图2（a）表示的是未进行位置校正时的误差曲线，从图上可以看出，位置误差最大值为9.12海里。我们选择在第10h和第16h分别利用外部位置和航向信息进行了两次校正，校正时的曲线见图2（b），图2（c）表示的是进行位置校正后的误差曲线，从图上可以看出，位置误差最大值为5.38海里。虽然从图中我们无法直观的看到对陀螺漂移的补偿情况，但是定位误差的累计主要是由陀螺漂移引起的。通过两次校正，定位精度得到了很大的提高，可以间接的证明陀螺漂移得到了有效的补偿，证明了本文提出的补偿方法是合理可行的。

图2（a） 未进行校正时的位置一次差曲线

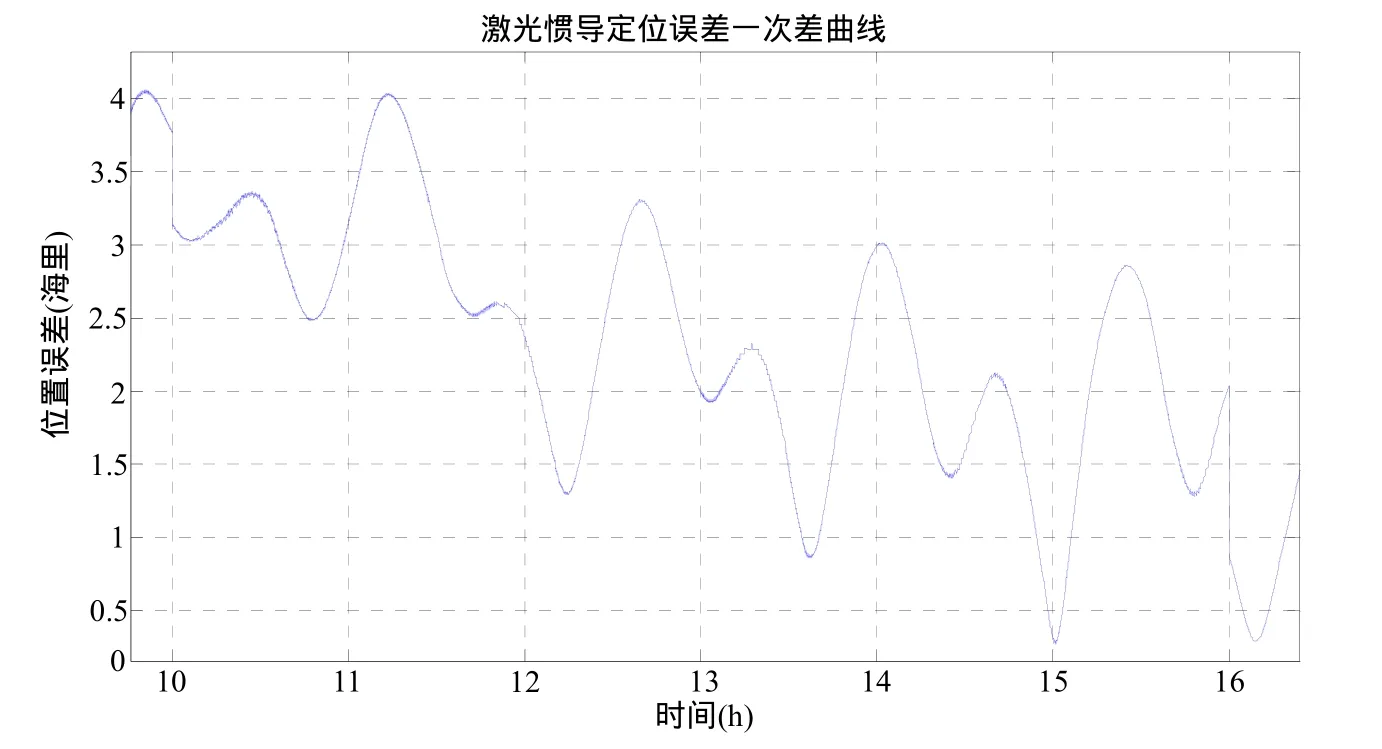
图2（b） 校正时刻的位置一次差曲线

图2（c） 进行校正的位置一次差曲线

4 结束语

本文从分析陀螺漂移对定位误差的影响出发，总结出惯导系统不论有没有旋转机构，陀螺漂移都是影响定位精度的主要原因。结合两点校思路，通过ψ角增量与观测量之间的关系，进一步建立起陀螺误差与观测量之间的关系。使用外部位置和航向参考信息，通过两次重调，即可计算出捷联惯导系统的陀螺漂移。通过试验结果验证了该算法的有效可行。

[1]黄德鸣,程禄.惯性导航系统[M].北京：国防工业出版社.1986

[2]张志涌等.精通MATLAB[M].北京：北京航空航天大学出版社.2003

[3]郑梓祯,蔡迎波.舰艇导航系统试验与鉴定[M].北京：国防工业出版社.2005

[4]于旭东,王宇,张鹏飞等.单轴旋转对惯导系统误差特性的影响[J].中国惯性技术学报.2008,16（6）：643-648

[5]可伟,乔海岩,孟凡强.船用激光陀螺惯导单轴旋转系统.舰船科学技术[J].2012,34（12）：67-71

[6]高延滨,管练武,王庭军等.单轴旋转式光纤捷联惯导系统定位精度分析[J].仪器仪表学报.2014,35（4）：794-799

[7]张鑫.长航时捷联惯导系统综合校正方法.舰船电子工程[J].2014,236（2）：47-51

[8]李魁,王玮,刘芳,等.长航时惯导系统全阻尼综合校正算法[J].仪器仪表学报.2012.33（3）：543-548

[9]赵龙,魏宇康,刘生炳,等.基于外测速度信息修正SINS姿态误差的H∞控制设计方法[J].导弹与航天运载技术.2014,334（4）：28-31