风电场代表年数据订正方法的不确定性分析

■ 谢今范 雷杨娜 孙娴

(1.吉林省气候中心；2.陕西省气候中心)

0 引言

运用合理的数据处理技术和方法对风电场风能资源评估是整个风电场建设、运行取得良好经济效益的关键[1，2]。有的风电场因风能资源评价失误而达不到预期的发电量，造成很大的经济损失[3]。

风电场往往只有一整年的现场测风数据，根据现场的测风资料所计算出的风能参数只能反映当年风能状况。由于中国是典型季风气候，冷暖季节较明显，加之地形条件复杂，风资源的波动性较大，年际变化明显，要评价风场的长期风能资源状况，必须根据能反映风场长期风资源状况的测风资料进行分析计算，因此场址附近长期测站的多年平均测风资料是必不可少的[4]。结合附近有代表性的长期测站的观测资料，将验证后的现场测风数据订正为一套反映风场长期平均水平的代表性数据进行风资源分析[5]。GB/T 18710-2002《风电场风能资源评估方法》[6]中明确规定风电场测风数据16方位代表年订正方法，目前大多数工程设计中也是用该方法进行代表年数据订正处理。但按照规范要求，风电场附近长期测站的测风数据与风电场现场测风数据的相关系数应达到0.80以上，方能用于数据订正。然而，对于地形起伏较大、气象站点分布相对稀少的地区而言，这一要求往往难以达到。

这种情况下，现行的订正方法是否仍适用，是否有替代或改进的订正方法，近年来也有学者在这方面展开了一些研究，但研究相对较少，研究成果也缺少一定的普遍意义。林芸[7]采用日平均风速作相关分析对云南某风电场进行数据订正，并对订正结果进行了合理性分析，指出在资料缺少的情况下利用该方法进行代表年订正是合适的。杜燕军等[4]以内蒙古地区某风电场风资源分析为例，探讨采用常规方法和改进方法对代表年风速的订正所产生的误差情况，改进了代表年订正方法，弥补了常规方法中的一些不确定因素对代表年修正结果的影响，减小了误差范围。王有禄等[8]分别利用国标GB/T 18710-2002《风电场风能资源评估方法》规定的风向相关法和另一种风速相关法对某风电场测风数据进行代表年订正，指出气象站与风电场风速相关性很差时，应通过多种方法计算分析后确定代表年结果。于兴杰等[5]采用风速年景划分法对风场风资源代表年进行订正，弥补了常规方法的不足，计算简单，便于应用。但该方法只能得到年风能资源，无法进行代表年风能资源的详细分析，且忽略了风场地形、地貌及气候等因素，对水平年在各方向上风速影响程度存在差异。路屹雄等[9]以江苏省为例，利用站点最大频数法和区域平均法对区域多站点的风能资源代表年进行选取，表明两种方法选取的江苏省风能代表年一致。但该方法仅是对具有较长时段观测数据的气象站点的代表性年份进行选取，对于仅有一年观测的风电场来说意义较小。

本文通过对某典型风电场测风塔测风数据和其周边气象站资料(风速、风向)的相关性分析，选定参证气象站对测风数据进行代表年订正，并对订正结果进行对比分析，系统全面地分析风电场代表年数据订正中的不确定性，研究在风电场代表年数据订正过程中产生误差的原因，以便将来对现有订正方法进行改进和完善。

1 资料与方法

本文数据选用某测风塔2009～2011年逐时风速、风向和距风电场最近的气象站同期及近30年的风速进行分析。风电场以浅沟壑地貌为主，北低南高，东西方向较为平坦。测风塔海拔高度约为1636 m，塔高70 m。气象站距风电场直线距离约为16 km，观测场海拔高度为1336 m，比风电场平均海拔高度低约300 m。本文主要采用回归分析、相关分析等统计分析方法。鉴于该风电场有两年以上(2009～2011年)的测风资料，为了分析不同时段代表年计算成果的差异，分别选择近20年、近10年两个时段及2009～2011年3个实测年数据进行代表年分析计算。

2 结果分析

2.1 气象站代表性分析

根据有关规定[8]，该气象站具有各气象要素的长期观测(30年以上)资料，近30年站址未迁移。观测场周围环境也未发生较大变化，观测数据的连续性、一致性、完整性较高，满足作为风场序列延长的参照站。如近30年(1982～2011年)平均风速为2.2 m/s，近20年(1992～2011年)平均风速为2.2 m/s，近10年(2002～2011年)平均风速为2.2 m/s。气象站多年平均风速见表1。

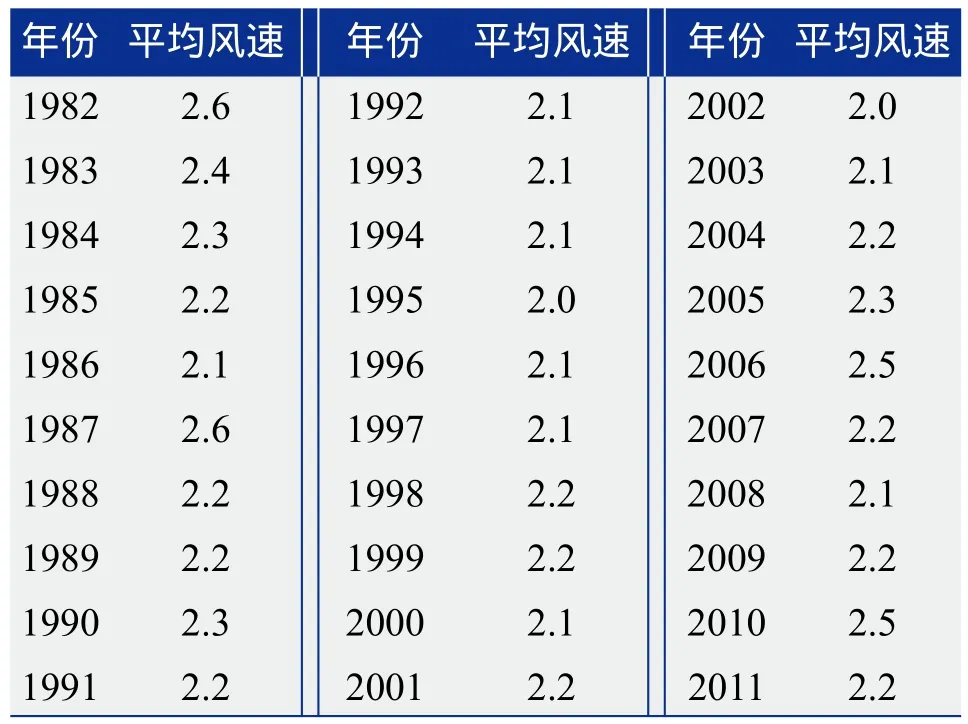
表1 气象站历年平均风速 (单位：m/s)

计算该气象站与测风塔同期相关系数见表2。由表2可知，不论是逐时风速、日平均风速、日最大风速，还是有效风速区间风速，气象站与测风塔相关系数均在0.45以上，相关性较好。另外，由于该站主要气候特征方面与风电场基本一致，故本文选择该县气象站资料进行区域性和代表性评价。

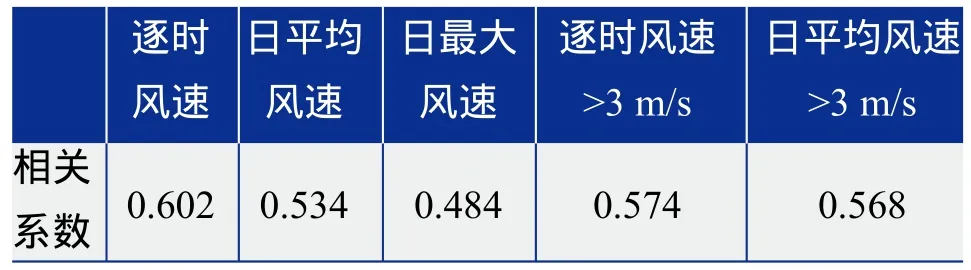
表2 气象站10 m与测风塔70 m同期相关系数

根据气象站2011年逐时风速实测数据与某风电场同期实测逐时风速数据，及QX/T 74-2007《风电场气象观测及资料审核、订正技术规范》[10]，将风电场短期测风数据订正为代表年风况数据，回归计算成果详见表3。测风塔70 m高风速与县气象站10 m高风速的相关系数，在16个方位中，除E、ESE和WSW 3个方位外，其他方位二者相关系数均大于0.7，16方位的相关系数均通过了0.01的显著性检验。相关系数较小的几个方位，可看出样本数也相对较少，对代表年数据的影响相对较小，因此认为用该气象站数据进行代表年数据订正基本可行。

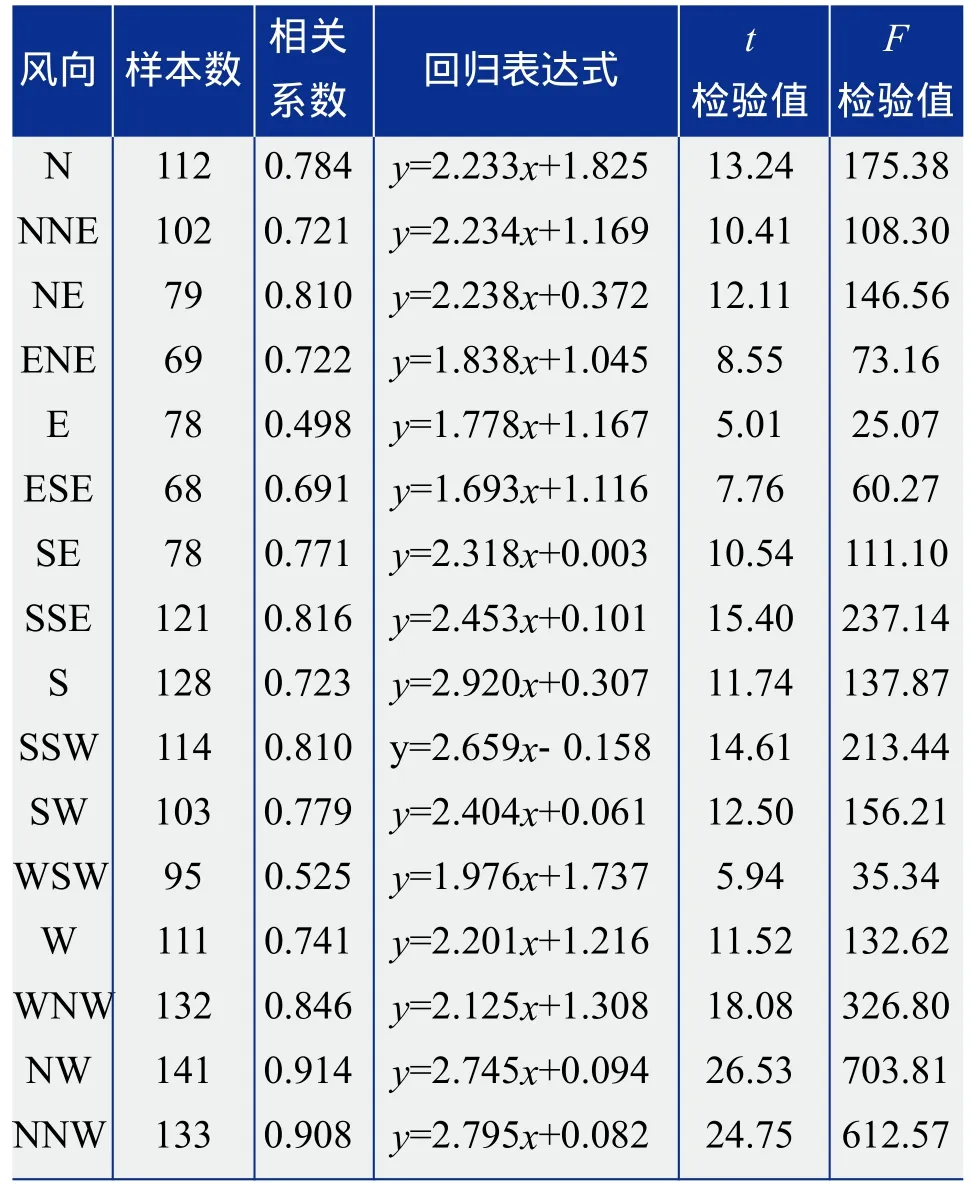
表3 测风塔70 m高度与气象站10 m高度风速16方位相关方程参数

2.2 测风塔观测年份不同导致的不确定性

2.2.1 测风塔不同时段代表年结果分析

分别利用测风塔2009～2011年实测逐时风速数据、气象站同期及近10年(2002～2011年)逐时风速实测数据，根据《风电场风能资源评估方法》，将风电场短期测风数据订正为代表年风况数据，相关系数计算结果详见表4。综合来看，测风塔70 m高风速与气象站10 m高风速的相关系数在2010、2011年相对较高，2009年则相对偏低。16个方位中，2009年在NNE～NE区间和E～SE区间相关系数均较小，在0.5以下，相关系数大于0.7的方位为9个；2010年仅ESE方位小于0.5，相关系数大于0.7的方位为10个；2011年仅E方位小于0.5，相关系数大于0.7的方位为13个。可见对于同一测风塔和同一气象站，选择不同年份作为观测年进行代表年数据订正时，各方位的相关系数存在一定差异，在测风塔观测时段较长时，可选择相关系数较高年份进行代表年数据订正，以期得到较准确的代表年数据结果。

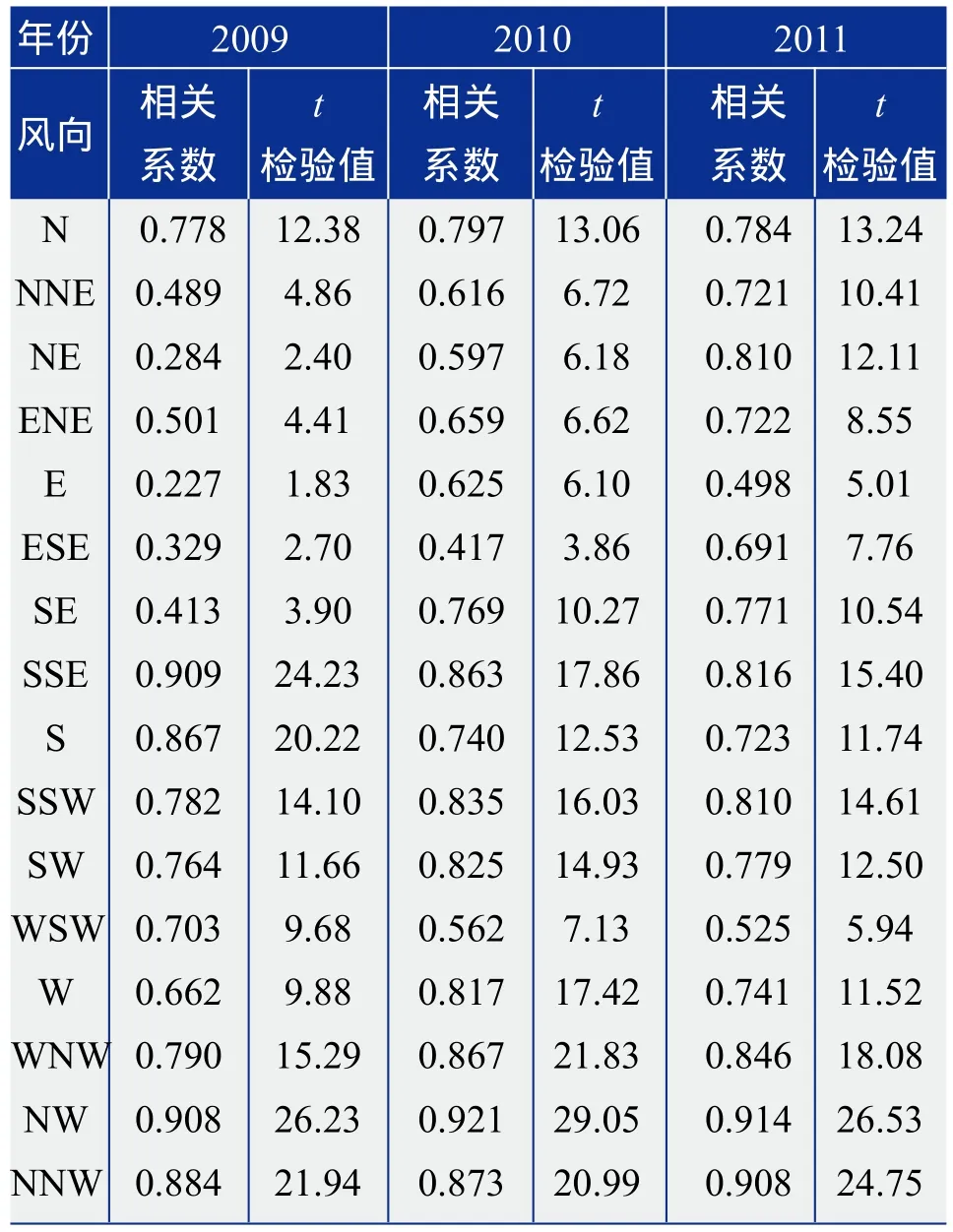
表4 测风塔2009～2011年70 m与气象站10 m风速16方位相关系数

利用测风塔2009年数据计算得到代表年平均风速为6.6 m/s，利用2010年数据计算得到测风塔代表年平均风速为6.2 m/s，而用2011年数据计算得到测风塔代表年平均风速为6.0 m/s。2010年与2011年计算得到的代表年数据相差较小，二者相差0.2 m/s，不到4%；而用2009年数据计算得到的代表年数据则与其他两个年份差距较大，相差7%～10%。从上述相关分析可知，2009年测风塔与气象站16方位相关系数较低，因此认为以2009年作为观测年计算测风塔代表年数据误差较大，在实际工作中不予采用。这也说明在利用气象站数据进行测风塔代表年数据订正时，要详细分析二者在16方位的相关性，以确定是否可采用《风电场风能资源评估方法》中规定的方法进行代表年数据订正。同时发现2010、2011年测风塔和气象站相关均较好，但在计算测风塔代表年数据时，得到的代表年风速仍存在差异。

2.2.2 原因分析

分别计算测风塔和气象站2010年与2011年各风向风速(图1)，分析塔、站这两年在风速和风向频率之间的差异。从图1可知，2010年和2011年风速差异主要出现在偏西北和偏东南方向。2010年测风塔和气象站在偏西北和偏东南方向上风速均大于2011年，但二者在2010年和2011年两个风向区间的风速差异大小并不一致，在W～NNW区间，测风塔2010年较2011年平均偏大18.7%，而气象站则偏大16.6%，偏大比例略小于测风塔；在SE～S区间，测风塔2010年较2011年平均偏大11.7%，而气象站则偏大10.7%。另外，可发现在偏西南方向，测风塔2010年风速仍较2011年偏大，而气象站在这个风向区间2010年和2011年无显著差异。测风塔和气象站在不同年份各风向风速差异上的不一致必然会对代表年数据计算造成一定影响。

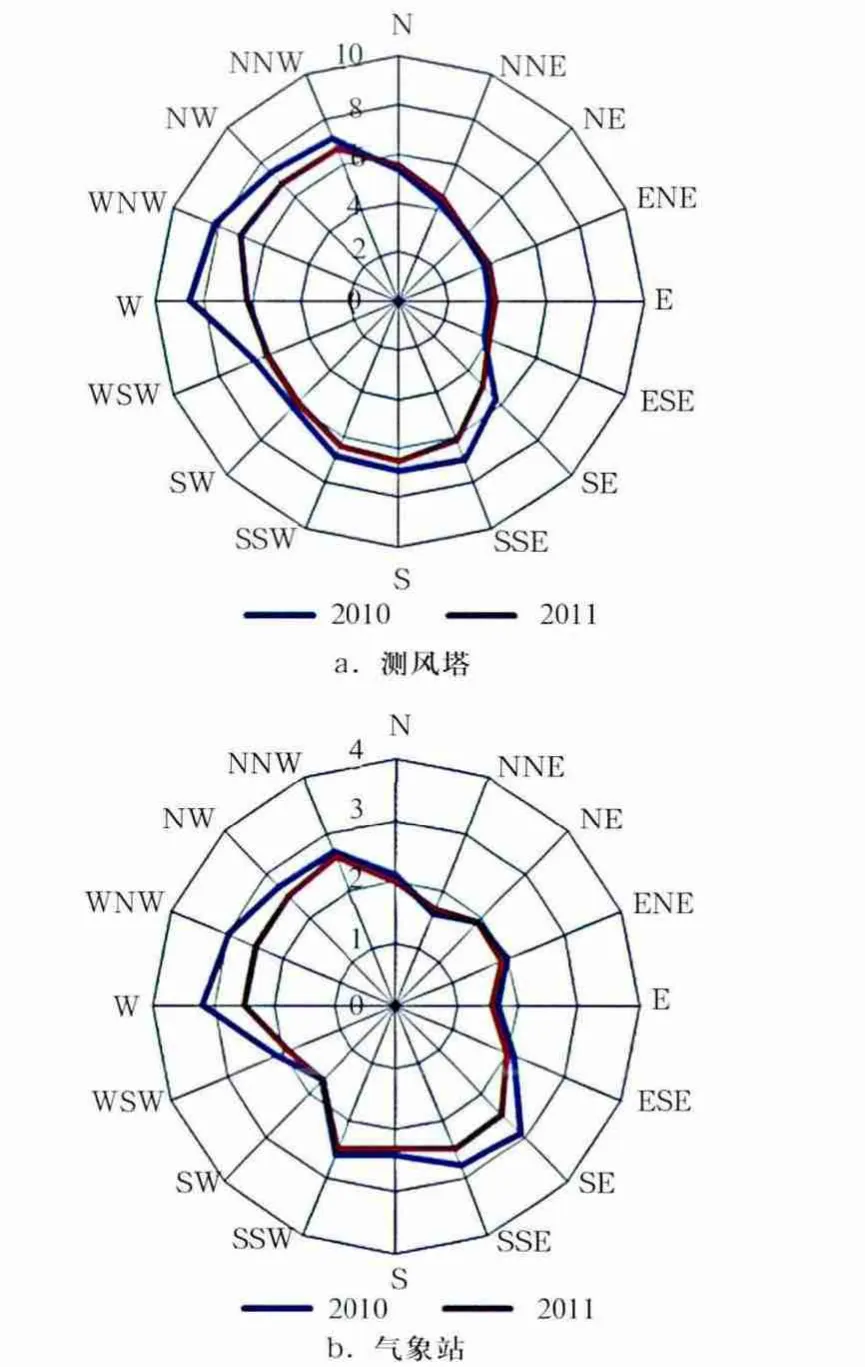
图1 测风塔(a)和气象站(b)2010年及2011年各风向风速(m/s)

分别计算测风塔和气象站2010年与2011年风向频率(图2)。由图2可知，2010年和2011年风向差异主要出现在偏西北方向和偏南方向。2010年测风塔和气象站在偏西北方向风向频率均大于2011年，在W～WNW区间，测风塔2010年较2011年平均偏大3.8%，而气象站则偏大2.8%，偏大比例略小于测风塔；在偏南方向，测风塔2010年与2011年差异主要在S～SSW区间，2010年较2011年平均偏小2.3%，而气象站则主要在S方向存在差异，2010年较2011年偏小1.5%。

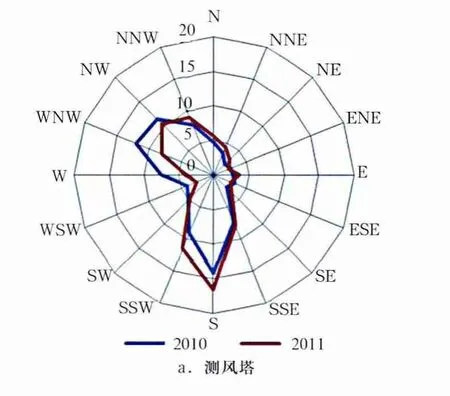
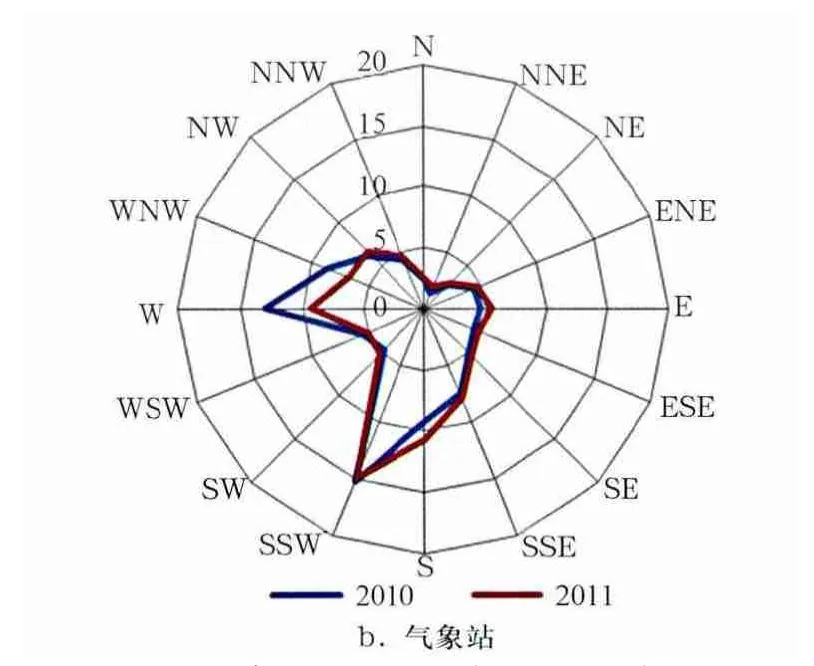
图2 测风塔(a)和气象站(b)2010年及2011年风向频率

此外，测风塔和气象站的主导风向并不完全一致。测风塔主导风向为S～SSW区间和W～NNW区间，在偏南方向，S方向风频较大，在西北方向，WNW方向风频较大；而气象站风向则主要分布在S～SSW区间和W～WNW区间，且以SSW和W方向风频较大。在进行代表年数据订正时，需对测风塔和气象站数据分16方位进行样本统计和回归方程计算，测风塔和气象站风向频率上存在的差异必然会对代表年数据计算结果造成一定误差。

2.3 测风塔和气象站风速变化的不一致性分析

《风电场风能资源评估方法》中测风塔代表年数据的计算方法，主要是分16方位利用线性回归方程进行计算，并未考虑二者风速变化不一致情况。事实上，测风塔各月风速变化与气象站各月风速变化趋势并不完全一致(见图3)。测风塔和气象站均是冬春季节风速较大，夏秋季节风速相对较小，但是测风塔风速季节变化显著，两气象站季节差异则较小。计算二者各月的风速差，发现6～10月测风塔风速较气象站偏大，均在4.0 m/s以下，而在1～5月和11～12月二者差值均大于4.0 m/s，说明测风塔和气象站的风速差异存在季节性。

测风塔和气象站风速的日变化趋势相反(图4)，发现测风塔风速在一日内呈先减后增趋势，即夜间风速较大，白天风速较小；而气象站风速则是先增后减，即白天风速较大，夜间风速较小。白天10：00～20：00为测风塔风速相对较小时段，而这个时段气象站风速则达到了一天中的峰值。

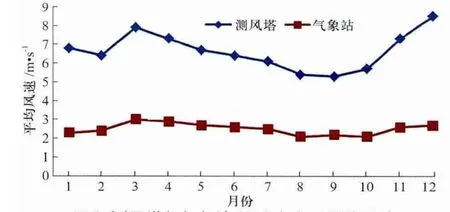
图3 测风塔与气象站2010年各月平均风速

由于测风仪器本身、周围外部环境、测风高度及风电场区域与长期气象站外部环境存在的差异，导致气象站风速变化与风电场区域风速变化存在上述差异。现有的测风塔代表年数据计算方法并未考虑这些差异，因此得到的代表年数据结果往往存在不确定性，加之无较长实测资料进行对比分析，很难对其误差进行订正；而且不同测风塔和相应的参证站风速及风向差异存在独特性，很难用统一的统计方法对现有代表年数据订正方法进行修正。

2.4 数值模拟数据的应用

从上述分析可知，很难用统计方法对现有代表年数据订正方法进行修正，但在风能资源评估中，因为不同测风年风速存在较大差异，仅用观测年数据进行风资源评估，不能代表风电场区域长期的风况。近年来，数值模拟技术在风资源评估中逐渐被广泛应用，美国、丹麦、加拿大、澳大利亚和日本等都先后开发和发展了许多较为成熟的应用数值模拟方法的风能资源评估系统软件[10-12]。中国也开展了相关研究，龚强等[13-15]、李晓燕等[16]、袁春红等[17]分别应用MM5模式、历史观测资料和中尺度大气模式相融合等方法进行了数值模拟方法在风能资源评估中的应用研究，获得很多经验。姜创业等[18]通过陕北模拟区实验分析，MM5/CALMET模式在复杂地形下模拟数据的可靠性，发现经过订正处理的模拟数据具有更好的真实性和可靠性。那长期的数值模拟数据能否代表测风塔长期的风况呢？

利用MM5/CALMET模式提取测风塔所在位置2009～2011年3年逐时风速风向数据，因模式数据存在系统误差，对于测风塔模拟数据，消除地形等影响的误差，分别以2010年和2011年为观测年，分24时次分别建立相关关系对数值模拟结果进行订正处理，得到测风塔2009～2011年的数值模拟结果(表5和表6)。实际观测2009～2011年测风塔平均风速为6.30 m/s，数值模拟结果分别为6.40 m/s和6.24 m/s，而以2011年和2010年为观测年，用国标方法计算得到的代表年结果分别为6.00 m/s和6.18 m/s。同实测值相比，数值模拟数据与实测值相差较小，仅为0.1 m/s和0.06 m/s，约1.7%和1.0%；而用气象站计算得到的代表年结果与实测值相差0.30 m/s和0.12 m/s，偏小5.0%和1.9%，相差较大。从各月风速比较来看，数值模拟结果除8月和12月相对误差较大外，其余月份相对误差都在5%以内。代表年数据除4～5月、8月和10月相对误差较小外，其余月份相对误差均较大，绝对值在5%以上，其中12月相对误差最大。整体来说，大部分月份代表年数据均小于实测数据，这也导致代表年数据整体偏小。

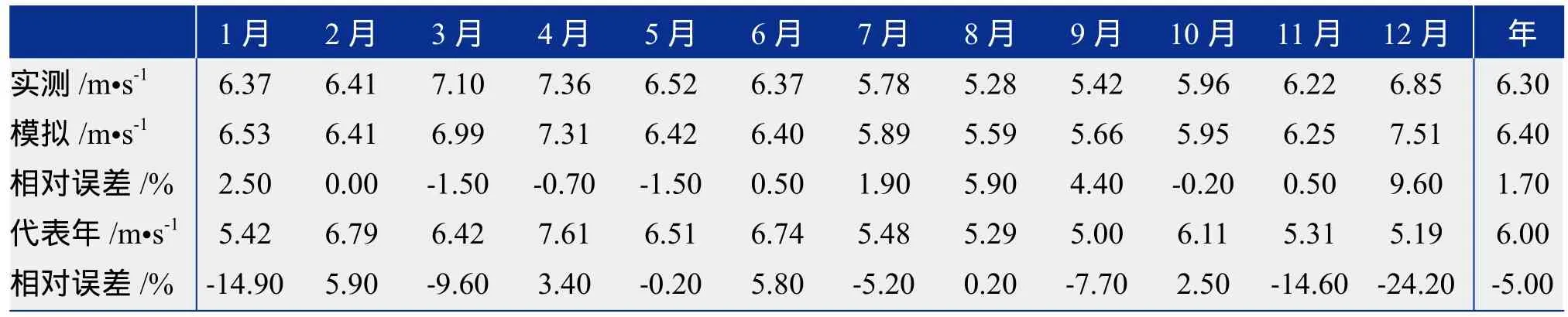
表5 数值模拟和实测2009～2011年及用2011年为观测年得到的近3年代表年风速数据

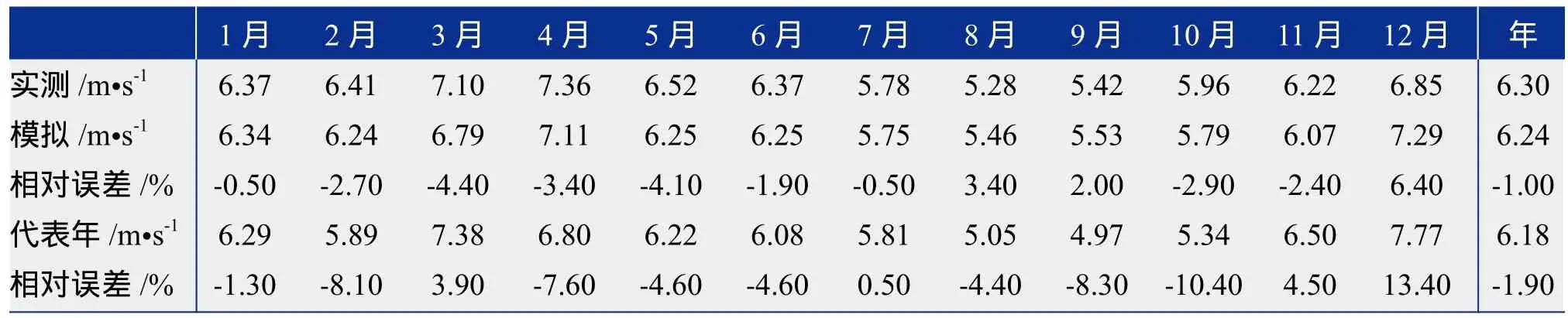
表6 数值模拟和实测2009～2011年及用2010年为观测年得到的近3年代表年风速数据

对比测风塔实测、数值模拟和代表年风速日变化，从图5可看出，各时次平均风速的变化趋势基本一致，均呈先减后增的日变化趋势，0：00～6：00 风速较大，早晨 7：00 开始减小，白天经历两个最低值，19：00风速开始增大，至凌晨增至最大。相对来说，数值模拟结果和实测数据在各时次相差较小，尤其是夜间，在白天和实测数据风速相差略大；而代表年结果整体来说各时次风速均小于实测值，且偏小较多。

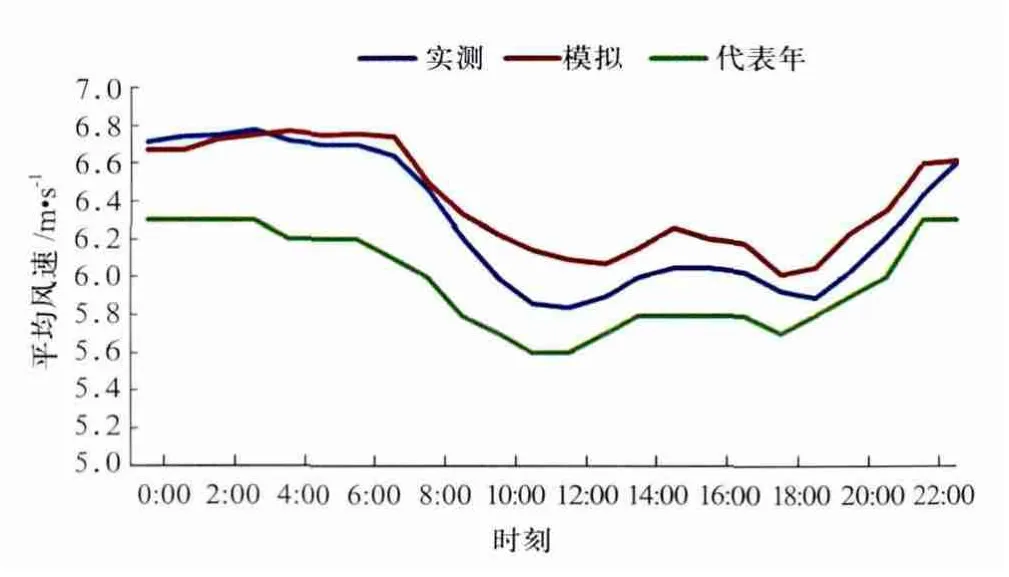
图5 测风塔70 m高度平均风速日变化

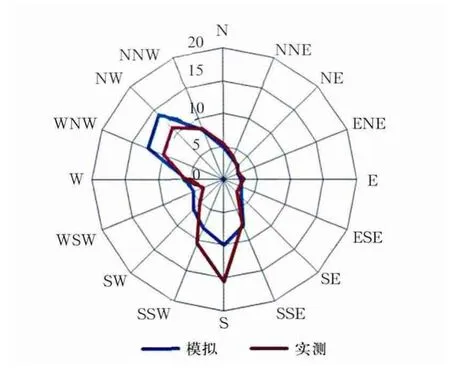
图6 测风塔实测和模拟的风向频率

对比测风塔2009～2011年实测和模拟的风向，可发现二者在主导风向上比较一致，均是WNW～NW和SSE～SW区间风向频率较大，说明数值模拟技术对风向的模拟比较准确。不同的是，数值模拟数据在偏西北方向风频大于偏南方向，而实测数据则是偏南方向大于偏西北方向。

另外，挑选了本地区6座测风塔，提取测风塔所在位置数值模拟资料，对比模拟资料和实测数据，计算模拟资料的误差(表6)，分析数值模拟资料在该地区的可用性。由表6可知，6座测风塔实测风速和模拟风速逐时值相关系数均在0.5以上，相关系数较高，二者差值基本在0.1以下，相对误差基本在2%以内，可见数值模拟资料与实测数据的误差较小，基本可代表测风塔所在位置的风速情况。

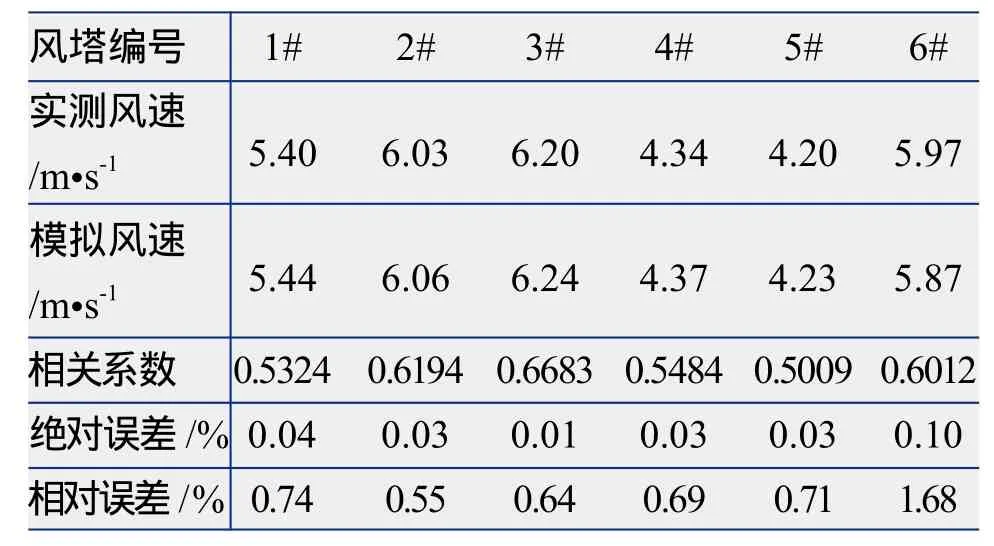
表6 6座测风塔70 m高度实测数据和模拟数据对比分析

图7 6座测风塔实测(蓝色)和模拟(红色)风向玫瑰图

对比6座测风塔实测和模拟的风向(图7)，可见除1#和4#测风塔外，其余几座测风塔模拟资料得到的风向频率和实测数据的风向频率分布基本一致，较好地模拟出了测风塔的风向分布情况。

综上分析可知，在本地区利用MM5/CALMET模式模拟测风塔位置的风资源情况，整体来说误差范围较小，风向分布的模拟与实测结果基本一致；气象站数据与风电场测风塔数据风速风向变化一致性较差的情况下，可尝试利用数值模拟技术对测风塔长期风况进行模拟，计算其模拟误差，分析数值模拟资料的合理性，判断是否可用数值模拟资料分析测风塔的长期风况。

3 结论与建议

1)分别利用测风塔不同年份(2009、2010和2011年)实测逐时风速数据、气象站同期及近10年实测数据订正得到的代表年风况数据差异较大，得到的代表年数据分比为6.6 m/s、6.2 m/s和6.0 m/s。当测风塔与气象站16方位相关性较差时订正得到的代表年数据代表性较差，不予使用；而当16方位相关性较好时，由于不同观测年测风塔和气象站在各风向风速和风向频率上的不一致性，仍会导致代表年数据结果出现不一致的情况。

2)气象站风速与风电场区域风速在月变化、日变化趋势上也存在一定差异，而现有测风塔代表年数据计算方法并没有考虑这些差异，因此利用16方位相关法得到的代表年数据结果往往存在不确定性。但大部分气象站有近20年的测风数据，从一般风电场20年的运行寿命来讲，利用气象站计算其代表年数据可得到近20年的平均风况，因此在气象站数据均一性较好、与测风塔风速风向变化情况一致性相对较高时，可选择用气象站数据计算测风塔代表年数据。

3)数值模拟技术在风资源评估中广泛应用，经验证可利用数值模拟技术模拟测风塔的长期风况，且二者差异较小，可较为客观准确地反应测风塔的长期风资源状况。但针对不同区域适用数值模式不一，需分析数值模式的适用性，计算过程相对繁琐复杂。因此在气象站数据均一性较差、与测风塔风速风向差异较大时，可适当选择合适的数值模式进行长期风况的模拟。

[1] 周荣卫， 何晓凤， 朱蓉. MM5/CAMLET模式系统在风能资源评估中的应用 [J]. 自然资源学报 ， 2010， 25(12)： 2101 －2112.

[2] 陕华平， 肖登明， 薛爱东. 大型风电场的风资源评估[J]. 华东电力 ， 2006， 34(2)： l5 － l8．

[3] 连捷. 风电场风能资源评估及微观选址[J]. 电力勘测设计，2007， (2)： 71 － 73．

[4] 杜燕军， 冯长青. 风电场代表年风速计算方法的分析[J]. 可再生能源 ， 2010， 28(1)： 105 － 108．

[5] 于兴杰， 孙金丹. 风电场风资源代表年分析法[J]. 中国勘察设计 ， 2012， 1： 62 － 64．

[6] GB/T18710-2002， 风电场风能资源评估方法[S]．

[7] 林芸. 云南山区风能资源观测数据订正方法初探[J]. 云南水力发电 ， 23(6)： 1 － 4.

[8] 王有禄， 沈檬. 风电场代表年风速系列计算方法的探讨[J].新能源 ， 2008， 6： 69 － 76．

[9] 路屹雄， 王元， 李艳. 江苏风能资源代表年选择的方法比较[J]. 气象科学 ， 2009， 29(4)： 524 － 526．

[10] QX/T 74-2007， 风电场气象观测及资料审核、订正技术规范[S]．

[11] Archer C L， Jacobson M Z. Evaluation of global wind power[J]. Journal of Geophysical Research， 2005， 110，D12110.

[12] Brower M， Bailey B， Zack J. Applications and validations of the MesoMap wind mapping system in different climatic regimes[R]. Proceedings of Windpower 2001， American Wind Energy Association， Washington， DC， 2001.

[13] 龚强， 袁国恩， 张云秋， 等. MM5模式在风能资源普查中的应用试验 [J]. 资源科学 ， 2006， 28(1)： 145 － 150．

[14] 李晓燕， 余志. 基于MM5的沿海风资源数值模拟方法研究 [J]. 太阳能学报 ， 2009， 26(3)： 401 － 408．

[15] 袁春红， 薛析， 杨振斌. 近海区域风速数值模拟试验分析[J]. 太阳能学报 ， 2004， 25(6)： 741 － 743．

[16] 谌芸 ， 田浩 ， 宗翔 ， 等 . 基于网格计算的 MM5 系统在青藏高原地区的应用[J]. 气象与环境科学， 2007， 30(1)： 4－9.

[17] 张鸿雁， 丁裕国， 刘敏， 等. 湖北省风能资源分布的数值模拟 [J]. 气象与环境科学 ， 2008， 31(2)： 35 － 38.

[18] 姜创业， 孙娴， 徐军昶． MM5/CALMET数值模拟在陕北风能资源评估中的应用 [J]. 中国沙漠 ， 2011， 31(6)： 1606 －1610．