失效卫星救援过程中相对导航算法研究

杨雪勤，王洪宇，冯 刚

（上海宇航系统工程研究所，上海 201109）

0 引言

太空中存在大量的失效卫星，这些卫星或是服务期已过，因一个或数个系统失效而成为废弃卫星，或某载荷失效而不能正常工作。对此类卫星，如无其他措施，将可能成为空间碎片或垃圾，其存在会威胁空间其他卫星的正常飞行。因此，空间救援与维护显得尤为重要。针对此类失效卫星的空间救援措施一般为：施援卫星轨道机动至救援目标附近，用其携带的机械臂实施救援，或用机械臂回收废弃卫星以减少空间垃圾或更换救援目标的载荷模块以重新使用。这些空间救援与维护策略，均需对救援目标实施近程逼近过程，施援卫星需装备近程导航设备实现对求援目标的相对导航与控制［1］。

非线性条件下的扩展卡尔曼滤波（EKF）对非线性的系统方程或观测方程进行泰勒展开，并取其一阶近似项，这样不可避免会引入线性化误差，当线性化假设不成立时，EKF算法会导致滤波器性能下降甚至造成发散［2］。在空间目标跟踪过程中，不能排除目标飞行器存在发生非合作性机动或大幅扰动的可能性。此时，目标将偏离原运行轨道，且在地心引力场的作用下这种位置和速度的偏离会呈现复杂的非线性特征。与此同时，传统的最优或次优滤波算法并不具备良好的抗扰动性，致使在突变扰动下难以持续对系统状态进行准确跟踪，从而导致跟踪算法呈现跟踪快速性的不足，甚至因算法不收敛而引起失跟。因此，研究适于轨道机动目标跟踪的滤波估计算法显得尤为必要。适于非线性系统的滤波器无味卡尔曼滤波（UKF）通过确定性采样得到的一组Sigma点，可获得更多的观测假设，对系统状态的均值和协方差的估计更准确，同时因采用非线性的状态方程或观测方程而避免了线性化误差［3］。在救援目标进行连续轨道机动时，对其进行轨道跟踪控制，观测量必然包含控制加速度信息，加速度偏差可等效为目标轨道机动过程中的动力学模型误差。对此，可将目标机动的控制加速度视作一不确定性干扰因素，用强跟踪性的UKF滤波算法削弱不确定性干扰因素的影响，实现对机动目标的自主随动跟踪过程中的高精度相对导航。针对近距离的空间救援目标出现机动状况，本文提出了施援卫星的自主跟踪过程中相对导航方案及其优化策略。

1 相对轨道动力学模型

对救援目标近程跟踪与逼近控制来说，建立两个飞行器间的相对轨道动力学模型是控制的基础，也是相对导航技术的基础［4－6］。

在惯性参考系中，目标器T和施援卫星S的轨道动力学方程分别为

T，S的相对几何关系如图1所示。位置关系可表示为

式中：为相对救援目标的编队向量；ΔrT／S为施援卫星相对编队向量点的位置矢量；lT／S为施援卫星相对救援目标的位置矢量。

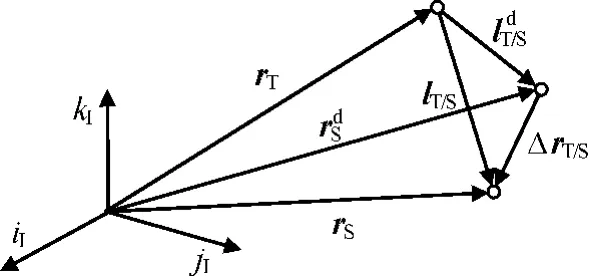
图1 空间两飞行器相对几何关系Fig.1 Relative geometry between two spacecrafts

式（2）减去式（1），并由式（3）、（4）可得

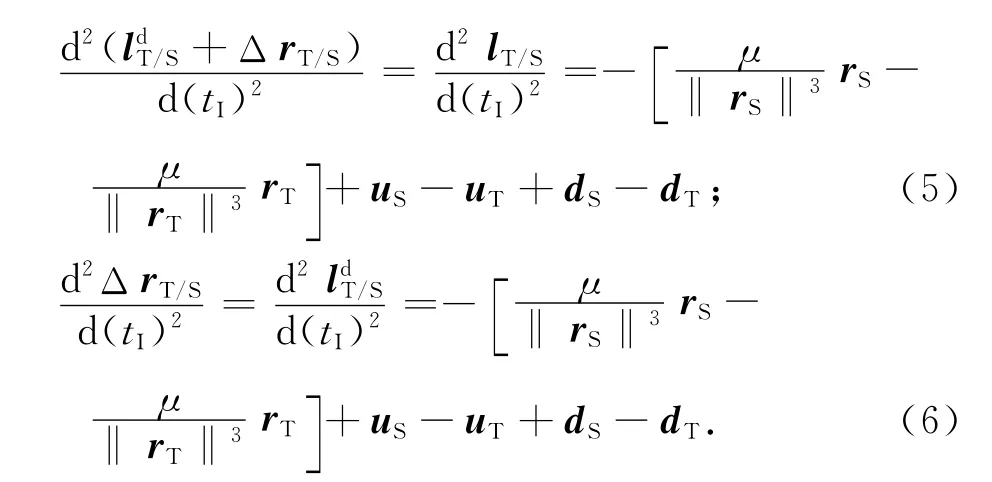
在目标轨道系中，由于两飞行器相距仅数十千米，可简化摄动影响，对两器间的引力差进行线性化简化处理。定义状态向量

将相对轨道动力学方程写成状态空间形式

式中：w为干扰量，且w＝［03×4fd3×1］T；uctrl为相对动力学方程中的加速度矢量，且uctrl＝uS－uT－；

此处：fd3×1为干扰加速度向量为与跟随位置矢量有 关 的 加 速 度 矢 量；A41＝。其中分别为救援目标角速度和角加速度；ω0为救援目标平均轨道角速度。

对救援目标自主跟踪问题，因目标的机动未知，为能有效跟踪控制，将目标机动隐含在扰动项内，即将uT隐含在w中，则uctrl＝uctrl＋。

2 相对导航设计

2.1 相对导航系统结构

施援卫星一般均装有近程跟瞄测量系统，可对救援目标进行视线距离、视线速度及视线方位角的相对测量。施援卫星的近程相对导航系统如图2所示。

图2 跟瞄相对导航系统Fig.2 Tracking and pointing relative navigation system

施援卫星携带的近程测量设备可以是主动式微波测量设备、被动式光学测量设备或主备组合一体的组合测量设备，能对求援目标进行相对测量。相对导航系统一般根据近程目标测量设备输出的两星间的视线距离、视线距离变化率、视线方位角和视线方位角变化率等测量信息，选取合理的测量信息，根据两星间的动力学模型，建立合理的测量方程，设计相对导航滤波器实现对两星间相对状态的估计，为目标近距离跟踪控制提供信息输入。

2.2 近程相对导航系统观测量与观测方程

2.2.1 近程跟瞄系统观测量

假设导航测量系统测量坐标系（如图3所示）与施援卫星的体轴系重合。星上跟瞄系统的测量输出为：目标相对施援卫星的视线距离及其变化率ρ，；视线在施援卫星跟瞄测量坐标系中的高低角α及其变化率（定义为视线与其在测量坐标系xy平面的投影间的夹角，抬头为正）；视线在施援卫星跟瞄测量坐标系中的方位角β及其变化率（定义为视线在测量坐标系xy平面的投影与x轴的夹角，偏向＋y轴向为正）。

图3 施援星上跟瞄设备测量坐标系Fig.3 Measuring coordinate system of tracking and pointing on satellite

式中：wρ，wα，wβ，w，w，w为跟瞄测量噪声，可视为相互独立的高斯分布的白噪声。

直接测得ρ，α，β，，，，则可得求援目标相对位置和速度在施援卫星体轴系中的分量为

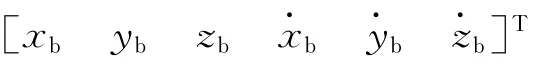
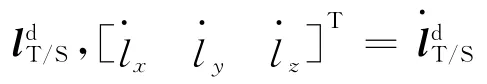
2.2.2 导航系统测量方程建立

式中：RSb／T为救援目标轨道坐标系至施援卫星体轴系的方向余弦阵；Vk为量测方程噪声阵。

因观测方程为非线性，有

此处：ωc为施援卫星轨道角速度；

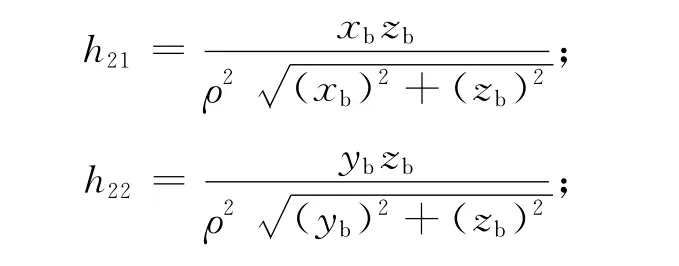
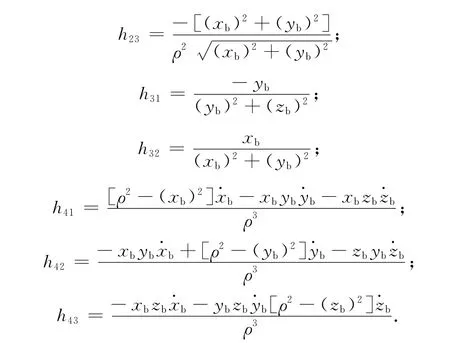
综合可得滤波观测方程

2.3 基于目标机动的相对导航滤波器优化设计

目标不机动时，一般救援星上相对导航系统方案多采用EKF设计，针对非线性的测量方程［式（26）］进行线性化处理，得到线性化观测方程［式（27）］［7］。因此，对非机动空间目标的常规相对导航算法，可认为观测量偏差主要是跟瞄设备测量噪声。对机动空间目标进行实时检测和相对运动状态估计，则还需考虑模型的不确定性。因控制加速度的量级远大于其他摄动加速度的误差量级，观测量中还包含了反映目标机动过程中的动力学模型误差。在扰动环境中，传统滤波算法会出现收敛慢甚至不收敛的状况，无法对实际相对运动状态进行准确的估计和预测。为此，需对星上EKF滤波算法进行优化，采用一系列对外部扰动具一定容忍度的强跟踪滤波算法，确保相对导航算法可在内部模型误差和外部扰动持续存在条件下保持稳定，并能在强扰动环境中对施援卫星与目标器间的相对运动状态做出准确估计。

另外，采用强跟踪的UKF滤波算法，可不用对非线性的测量方程进行线性化，能显著简化算法。

2.3.1 基于强跟踪的相对导航UKF滤波算法

UKF法采样的粒子点（一般称Sigma点）的个数很少，具体数量取决于选择的采样策略［8］。具体步骤为：考虑一个L维的随机变量x，且满足非线性方程y＝g（x），假设x有均值和方差Px，为计算y的统计特性，现生成2L＋1个Sigma点xi及相应权值Wi，输入维数j＝2，…，n时，迭代公式为

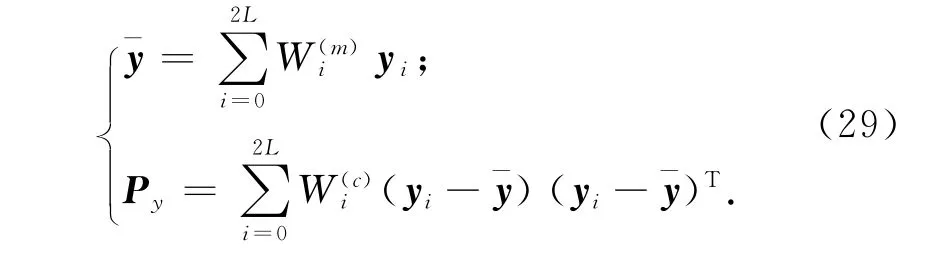
对非线性系统

式中：xk为状态量；yk为观测量；uk为控制量；wk为状态过程噪声；vk为观测噪声。假设wk，vk为高斯白噪声，且wk∈N（0，Q），vk∈N（0，R），wk，vk互不相关。则UKF滤波算法步骤如下。

a）初始化

b）计算采样点。用均值－1和方差Pk－1，计算2L＋1个采样点xi，k－1，有

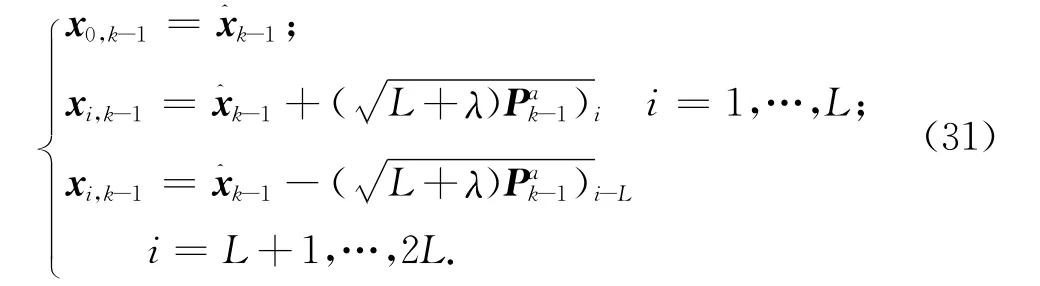
c）时间更新

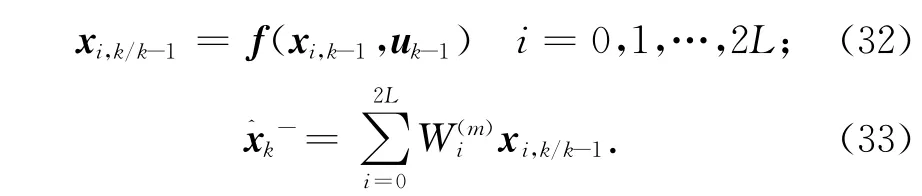
一步预测方差

系统预测观测值

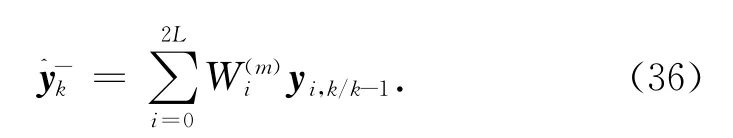
d）测量更新

2.3.2 STUKF

对定义的非线性系统，使滤波器成为强跟踪滤波器的一个充分条件是在线选择时变增益阵K（k＋1），使

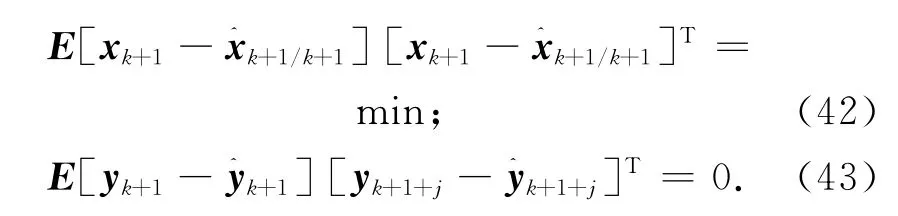
式中：k＝0，1，2，…；j＝1，2，…［8-9］。

其中要求残差序列处处保持相互正交，此处正交性原理的实质是在状态残差估计最小方差性能指标的基础上再附加一个输出残差序列处处保持相互正交的性能指标，物理意义是当系统参数失配时，可通过残差序列表现出，通过在线调整K（k＋1），迫使残差序列具正交性，从而保持对实际系统状态的跟踪。

STUKF算法是在通过在协方差阵中引入一时变的渐消因子，一步预测误差协方差阵变为

式中：λk为时变因子，λk≥1，且

此处：

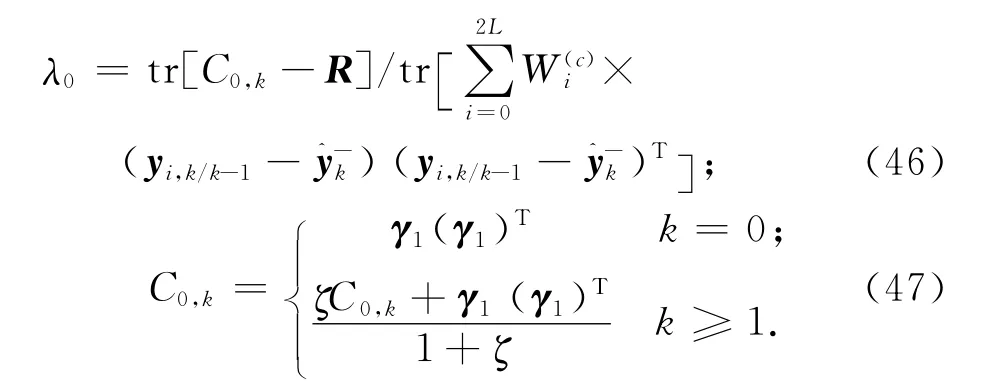
其中：γk为残差序列，且γk＝yk－（k＝1，2，3，…）；ζ为遗忘因子，且0＜ζ≤1。ζ能进一步提高滤波器的快速跟踪能力，其值越大，则时刻k以前的信息所占比例就越小，当前残差向量的影响越突出。

该方法有极强的关于突变状态的跟踪能力，并在滤波达到稳态时，仍保持对缓变状态以及突变状态的跟踪能力。

具体处理时，对λk可设定一上限值λmax，即

3 仿真分析与验证

设施援卫星位于目标飞行器后方10km处稳定伴飞，跟瞄系统对目标进行稳定测量，仿真开始3 000s后，求援目标器x轴轨道机动100s后停止机动稳定飞行。因本文不涉及跟踪控制，只是优化了原相对导航算法，仿真过程中相对控制仍为原设计。取仿真条件如下。

a）施援卫星和目标器在J2000系中的位置速度见表1。

b）跟瞄单机的测量精度为（3σ）：测距15m；测角0.2°；测速0.1m／s。近程相对导航的解算周期为0.4s，轨控周期为0.4s。

c）救援目标整器质量1 000kg，用于轨道控制机动的发动机推力5N，轨道控制加速度0.005m／s2。

用优化的STUKF滤波算法，施援卫星在目标卫星后方10km跟踪伴飞及目标突然机动过程中，仿真结果如图4～7所示。

由图4、5可知：稳定跟踪约3 000s后，目标突然＋x轴机动，轨道抬高，＋x轴相对状态增大，约600s后相对状态又恢复至10km附近，说明相对导航采用强跟踪UKF滤波算法优化后，对目标机动时两星相对状态进行了正确估计，使相对控制能在目标机动后仍能对目标进行跟踪伴飞。

表1 初始位置和速度Tab.1 Initial position and velocity

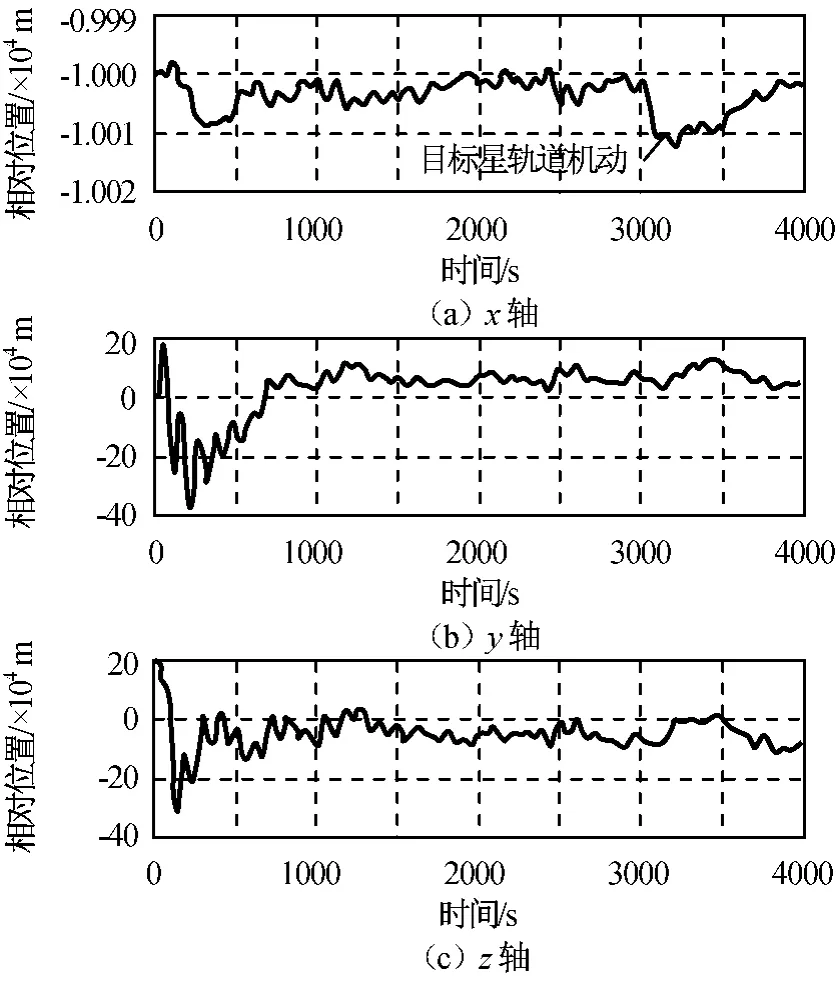
图4 两星相对位置Fig.4 Relation position of two spacecrafts

图5 两星相对速度Fig.5 Relation velocity of two spacecrafts

由图6、7可知：相对导航对三轴的相对位置估计和相对速度估计精度较稳定，三轴相对位置估计精度优于±20m，三轴相对速度估计精度约±0.1m／s。

图6 近程两星相对导航位置估计误差Fig.6 Relative position estimation error of two spacecrafts

图7 近程两星相对速度估计误差Fig.7 Relative velocity estimation error of two spacecrafts

综上，可认为用STUKF强跟踪滤波器，对突发增大的外部干扰具一定的强跟踪能力，相对导航滤波精度稳定，并未出现振荡。

4 结束语

针对施援卫星的近程相对系统，本文对常规使用的近程相对导航EKF算法进行了滤波器的优化设计。将星上近程跟瞄设备作为量测，对目标进行视线角距的测量，自主获取目标量测信息，并对两星的相对状态进行精确跟踪和估计，以作为近程跟踪控制的信息输入。设计了具强跟踪性的STUKF滤波器，优化了近程相对导航算法，目标机动时相对导航系统在不确定干扰影响下，仍能根据跟瞄系统的测量对两器的相对状态进行高精度估计。采用STUKF滤波算法，无需对非线性测量方程进行线性化处理，简化了运算，有一定的工程参考价值。

［1］ 李元凯.空间救援目标自主随动跟踪与控制研究［D］.上海：上海交通大学，2010.

［2］ KALMAN R E.A new approach to linear filtering and prediction theory［J］.Trans ASME Journal of Basic Eng，1960，82D：35-46.

［3］ JULIER S J，UHLMANN J K.A general method for approving nonlinear transformations of probability distributions［C］／／Proceeding of the 1996American Control COnference.［s.l.］：［s.n.］，1996：1628-1632.

［4］ 邢光谦，冯 刚，张宝恒，等.一种追踪飞行器近程逼近目标及保持伴飞的实现方法［P］.中国：ZL 200910125447.

［5］ 车汝才，张洪华，跟踪空间非合作目标的一种相对轨道确定方法研究［J］.中国空间科学技术，2007，27（4）：7-13.

［6］ 林 健，林晓辉，曹喜滨.基于自适应卡尔曼滤波的机动目标自主轨道确定［J］.上海航天，2008，25（2）：14-18.

［7］ 刘建业，赵 伟，熊 智.导航系统理论及应用［M］.南京：南京航空航天大学出版社，2005：248-281.

［8］ 刘 铮.UKF算法及其改进算法的研究［D］.长沙：中南大学，2009.

［9］ 刘华普，孔金生，董文丽.改进的强跟踪自适应滤波信息融合方法［J］.传感器与仪器仪表，2007，23（7）：141-143.