非合作目标卫星三臂型对接机构及其力学分析
2015-12-31李隆球张广玉柏合民
李隆球,张广玉,柏合民,陈 萌,范 佐
(1.哈尔滨工业大学 机电工程学院,黑龙江 哈尔滨 150001;2.上海市空间飞行器机构重点实验室,上海 201109)
0 引言
空间对接是指目标与追踪飞行器在完成交会后,在空间轨道上接近、接触、捕获和校正,紧固连接成一个复合的飞行器整体以及最后分离的过程[1]。空间对接是实现空间站在轨建造和运营,发展深空探测,实现航天器在轨加注、在轨模块更换、在轨维修等在轨服务的关键技术[2]。20世纪60年代,前苏联首先实现了宇宙-186与宇宙-188无人航天器的自动交会对接[3]。中国在2011年11月实现了神舟八号飞船与天宫一号目标飞行器空间交会对接。这两种对接以及与空间站等的对接都属于大型航天器的合作目标对接。空间非合作目标是指不是为对接或捕获设计的任一航天器,即该目标上不安装用于机械臂捕获的抓持机构(手柄)以及用于辅助测量的合作标志器和特征块,或不能进行姿态控制,在空间自由翻滚的任一航天器。一般包括己方未装置合作部件的卫星、己方装置合作部件但燃料耗尽或姿轨控系统故障的卫星、己方失效卫星、空间碎片,以及对方航天器等,现有的在轨航天器基本属于非合作目标[2]。
非合作对接目标因未安装对接接口,给对接机构的设计带来很大难题,但非合作目标对接技术在军事、商业及民用太空系统有巨大价值。卫星造价昂贵,一般是因控制位姿所需的燃料消耗殆尽而结束寿命,但卫星的通信、导航系统功能仍完好[1]。巨大的商业价值使欧、美、日等国正致力于此项技术的研究,并取得一定成果。轨道寿命延长智能航天器(SMART-OLEV)是由欧洲在轨卫星服务有限公司(OSSL)、瑞典 Space公司、德国 Kayser-Threde公司及西班牙Sener公司共同研制的在轨服务系统[2]。SMART-OLEV 针对的主要目标是地球静止轨道上燃料耗尽或姿轨控系统故障的通信卫星,其主要工作过程和功能是:在与目标卫星交会后,将捕获装置插入目标卫星的远地点发动机中,通过扩展头部的探针与目标卫星锁定,并拉动探针将目标卫星拉近,对接时用锁定装置帮助进行加固,为其提供推进、导航、制导和控制,使目标卫星保持合适的轨道和姿态,使其有效载荷继续发挥作用。2003年,ORC公司、荷兰宇航局(Dutch Space)和德国宇航局(DLR)联合启动了ConeXpress OLEV计划,最主要目标就是进行在轨维护及轨道间转移等[4]。美国国防高级研究计划局(DARPA)在1999年就公布了轨道快车(Orbit Express)计划[5-6]。该计划主要目的是在轨验证一系列技术,以满足在轨航天器燃料补给、系统改进和重构的需求。该计划已在2007年3月成功发射试验卫星2颗,试验自主交会、捕获与对接,卫星对卫星输送燃料以及替换星上设备等先进技术。日本的ETS卫星系列中,ETSVII卫星所采用的弱撞击对接机构已进行了飞行试验[2]。它由主动卫星和目标卫星组成,该对接机构属于弱撞击对接机构,采用碰锁和卡爪进行捕获和连接,碰撞力小,但对交会控制要求高。
实现对空间非合作目标卫星的捕获,可为其提供位置保持、姿态控制、轨道修正、离轨等操作,还能提供在轨维修、更换模块、燃料加注等服务,因此实现对其有效捕获和对接有重要的意义。美、欧、日等发达国家已取得了一定的研究成果,我国在非合作目标对接方面刚起步。本文针对非合作目标卫星的结构特点,选择发动机喷管作为对接接口,对一种三臂型卫星对接机构设计进行了研究。
1 对接目标选择及对接机构设计
1.1 对接目标分析及选择
本对接机构将目标飞行器选为地球同步轨道(GEO)卫星,因该类卫星数量最多,种类齐全,研究也最具代表性[7]。虽然,非合作目标卫星不能提供标准的抓捕和对接设施,但每个地球同步卫星均配备远地点反推发动机(AKM),其作用是将卫星从同步转移轨道送入地球同步轨道,且使用后一般不会再被使用[8-9]。因此,本研究选择远地点反推发动机喷管作为对接接口。AKM喷管近似锥形,标准喷管所需的测量数据及喷管的尺寸范围如图1所示[8-9]。图中:R2为喷管出口半径;RT为喷管喉径;α为喷管锥角;L为喷管长度。AKM喷管尺寸见表1。

图1 某AKM喷管尺寸参数Fig.1 Geometrical parameters of some AKM nozzle

表1 喷管尺寸Tab.1 Nozzle dimension
1.2 非合作目标卫星对接机构设计

图2 对接机构工作原理Fig.2 Principle of docking mechanism
本机构对接原理是建立一个封闭区域,如图2所示。图中:Δφ为两飞行器径向相对偏角;Δr为对接机构轴线与喷管出口面交点至喷管中心线的距离。因对接机构的工作环境是零重力状态,故在对接机构接近喷管的过程中,对接机构与喷管间不能有任何碰撞,否则会导致目标卫星飞离对接位置。喷管被包络于封闭区域中,这样就使喷管处在一无法逃脱的空间内,通过顶部平台上推与机械臂下压卡紧喷管,从而实现对接。
由于建立了封闭区域,该对接在与目标接触前已将目标位置锁定,使目标处在一无法逃脱的空间内,且封闭区域可容忍较大的径向和角度偏差,对机械臂的控制精度要求不高。
根据对接机构的工作原理、喷管大小和对接机构的技术要求,本文设计了一个三臂型对接机构,如图3所示。该对接机构包括支架机构、机械臂和末端执行器三部分。

图3 非合作目标卫星对接机构Fig.3 Model of docking mechanism for an uncooperative target satellite
2 对接过程仿真
在对接过程中,对接机构需完成靠近目标、肩关节展开、肘关节合拢、接触并捕获、固化两个飞行器、对接机构返回初始位置。
在两飞行器Δφ=8°,两飞行器轴向相对距离SA=300mm,Δr=30mm初始条件下,ADAMS软件仿真所得整个对接过程顺序如图4所示。由图可知:该对接机构能对目标很好地进行捕获和对接,顺利完成了整个对接过程。
3 对接机构运动学分析
本文设计的对接机构中,机械臂的结构最复杂,也最重要,是整个对接机构的执行机构和核心部分,捕获和对接的动作最终由机械臂实现。因此,机械臂的运动学和动力学分析和轨迹规划是实现对机械臂控制的基础。
3.1 正运动学分析
运动学正问题是指对一给定的机械臂,已知杆件几何参数和关节角矢量求机械臂末端执行器相对于参考坐标系的位置和姿态。
3.1.1 坐标系建立和参数确定
本文的三臂型对接机构呈对称分布,3个机械臂的结构和控制相同,因此仅需对其中一个机械臂进行运动学分析即可。DENAVIT,HARTENBERG提出了一种矩阵代数方法解决机械臂的运动学问题:D-H矩阵法。它能表达动力学、计算机视觉和比例变换问题,其数学基础是齐次变换,具有直观的几何意义[10]。因在分析运动学时D-H矩阵法有诸多优点,本文用此法分析,建立坐标系如图5所示。该机械臂有转动关节4个和平动关节1个,转动关节轴分别为Z0,Z1,Z2,Z4,Z5,其中Z3为平动关节轴,建立了D-H矩阵参数表[11]。根据机械臂所建坐标系和其固定参数见表2。表中:li-1为Zi-1轴至Zi轴沿Xi-1轴测量的距离;αi-1为从Zi-1轴至Zi轴绕Xi-1轴旋转的角度;di为从Xi-1轴至Xi轴沿Zi轴测量的距离;θi为从Xi-1轴至Xi轴绕Zi轴旋转的角度。

图4 对接过程顺序Fig.4 Sequence of docking process
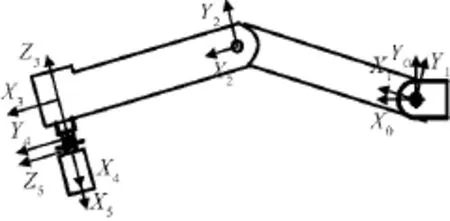
图5 机械臂坐标系Fig.5 Manipulator arm’s coordinate system
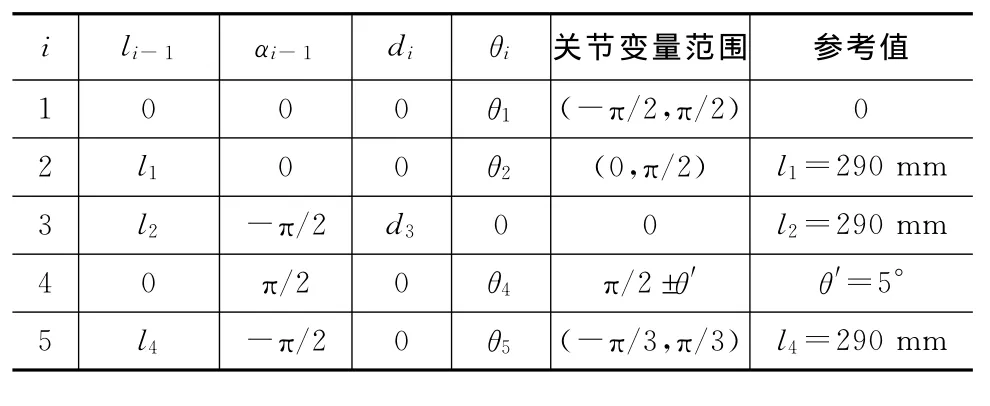
表2 D-H矩阵参数Tab.2 D-H’s parameters
3.1.2 基本坐标变换
设连杆坐标系{i}相对{i-1}系的变换矩阵为连杆变换矩阵。根据机械臂D-H坐标系,建立连杆的变换矩阵,它依赖于参数θi,li,αi,di。对转动关节i,为θi的函数;对移动关节iT为di的函数。变换矩阵可表示为
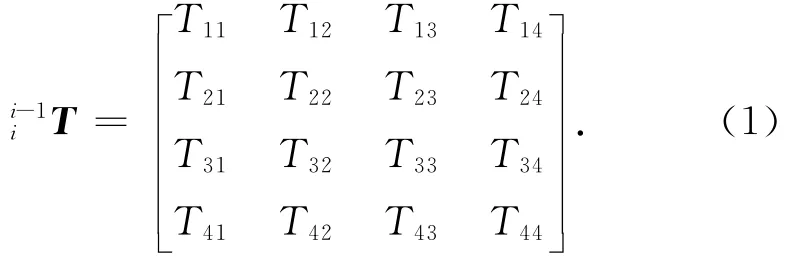
式中:T11=cosθi;T12=-sinθi;T13=0;T14=li-1;T21= sinθicosαi-1;T22= cosθicosαi-1;T23=-sinαi-1;T24=-disinαi-1;T31=sinθi×sinαi-1;T32= cosθisinαi-1;T33= cosαi-1;T34=dicosαi-1;T41=0;T42=0;T43=0;T44=1。将表2中数据代入式(1)可得


3.1.3 机械臂正运动学方程
根据求得的变换矩阵(i=1,2,…,n)。根据前面的分析可知:所有变换均相对动坐标系,根据从左到右的原则,可求出机械臂最后一个连杆(手抓坐标系)相对参考坐标系的位姿,即变换矩阵。此时只要给定关节变量,就可求出机械臂末端的位姿,机械臂运动学正解得解。

式中:c12=cos(θ1+θ2);s12=sin(θ1+θ2);p1=l2cos(θ1+θ2)-d3sin(θ1+θ2)+l1cosθ1;p2=l2sin(θ1+θ2)+d3cos(θ1+θ2)+l1sinθ1;c124=cos(θ1+θ2+θ4);s124= sin(θ1+θ2+θ4);p3=l2cos(θ1+θ2)-d3sin(θ1+θ2)+l1cosθ1;p4=l2sin(θ1+θ2)+d3cos(θ1+θ2)+l1sinθ1;p5=cos(θ1+θ2+θ4)cosθ5;p6=-cos(θ1+θ2+θ4)×sinθ5;p7=l4cos(θ1+θ2+θ4)+l2cos(θ1+θ2)+d3sin(θ1+θ2)+l1cosθ1;p8=-sin(θ1+θ2+θ4)×cosθ5;p9=-sin(θ1+θ2+θ4)sinθ5;p10=l4×sin(θ1+θ2+θ4)+l2sin(θ1+θ2)-d3cos(θ1+θ2)+l1sinθ1。

这与图6所示情况一致。
3.2 逆运动学分析
逆运动学问题是机械臂运动规划和轨迹控制的基础,已知机械臂杆件的几何参数,给定机械臂终端位姿,求各关节变量,称为机械臂逆运动学问题[12-13]。逆运动学包括存在性、惟一性及解法三个问题。
已知机械臂的位姿表达式为
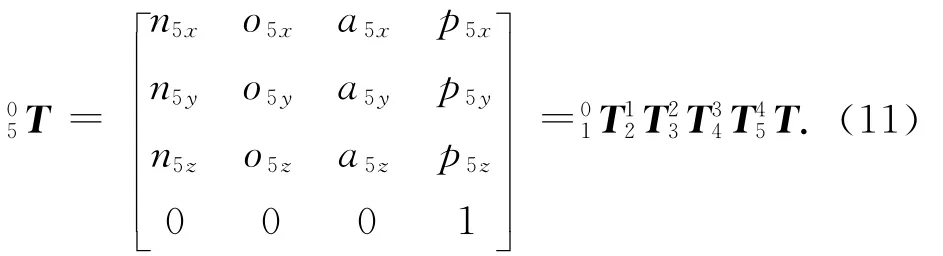
式中:n5x,n5y,n5z为末端操作器的法向矢量n5的三轴分量;o5x,o5y,o5z为末端操作器滑动矢量o5的三轴分量;a5x,a5y,a5z为末端操作器接近矢量a5的三轴分量;p5x,p5y,p5z为末端操作器位置矢量p5的三轴分量。比较式(10)、(11)可得

由坐标系间的关系,可得[o5xo5yo5z]=[0 0 1]。
由式(2)有

式中:p11=n5xcosθ5-o5xsinθ5;p12=-n5xsinθ5-o5xcosθ5;p13=p5x-n5xl4cosθ5+o5xl4sinθ5;p14=n5ycosθ5-o5ysinθ5;p15=-n5ysinθ5-o5ycosθ5;p16=p5y-n5yl4cosθ5+o5yl4sinθ5;p17=n5z×cosθ5-o5zsinθ5;p18=-n5zsinθ5-o5zcosθ5;p19=p5z-n5zl4cosθ5+o5zl4sinθ5。比较式(13)、(9)可得

式中:
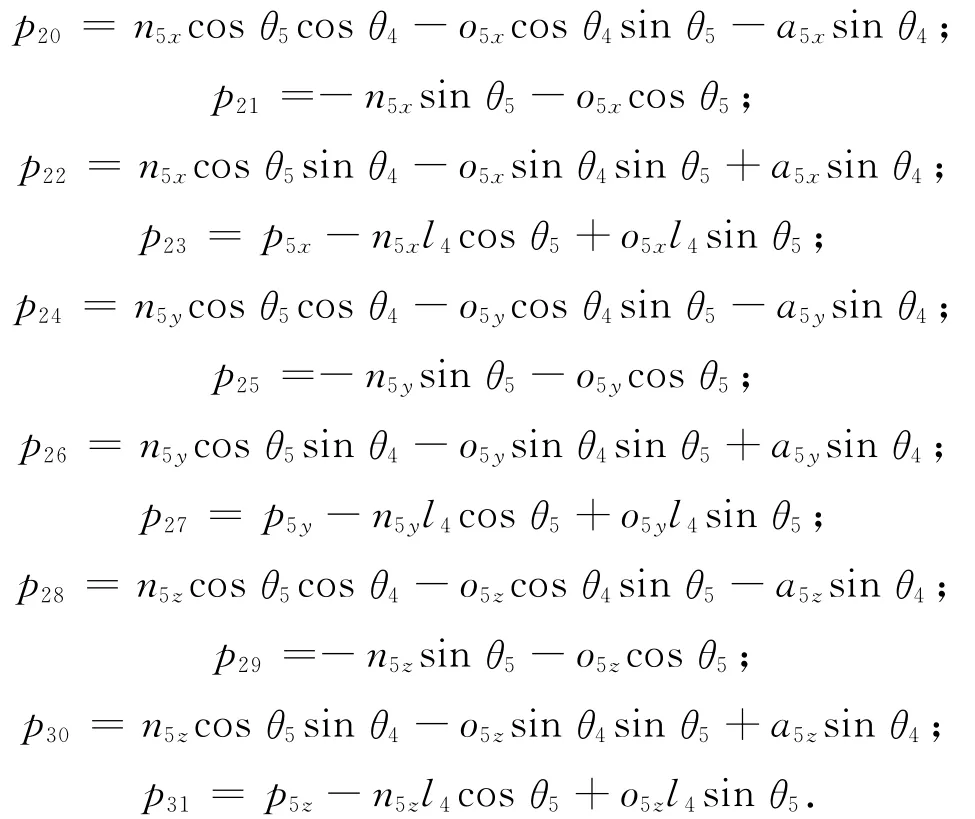
根据矩阵相等则对应元素也相等原则,有

对本机械臂,存在两个平行坐标轴z0,z1,y2,机械臂逆运动学分析简图如图6所示。图中:L1=L2=l。

图6 机械臂逆运动学分析简图Fig.6 Arm inverse kinematics analysis
根据几何关系有

当O0O3=L1+L2时,θ2=0,此时tanθ1=p3y/p3x,由此得出

由式(11)有

当O0O3<L1+L2时,可由几何关系得出

由式(16)可知:求解计算中包含了逆运动学多解问题,实际情况仅有一组合理的解,因此需剔除多余的解。剔除原则为:根据关节运动空间选择合适的解;选择与前一采样时间最接近的解;根据避障要求选择合适的解;逐级剔出多余解。

因此,从机械臂末端位姿矩阵,就可求出机械臂对应各关节角度θi。

表3 逆运动学解方程Tab.3 Solution of inverse kinematics equation
4 机械臂动力学分析
机械臂动力学研究的是机械臂的运动与关节驱动力(矩)间的动态关系。拉格朗日法不仅能以最简单的形式求得非常复杂的系统动力学方程,而且具有显式结构,物理意义较明确,适于分析相互约束下的多个连杆运动[13]。因此,本文采用拉格朗日法进行动力学分析。
由于结构的复杂性,其动力学模型也会很复杂,很难实现基于动力学模型的实时控制。但高质量的控制应基于被控对象的动态特性,因此须合理简化机械臂动力学模型,使其适于实时控制的要求。简化过程为:机械臂各构件为刚性;将杆件质心集中在杆件几何中心处;本机械臂是在微重力环境中工作,动力学分析时不考虑势能的影响;当机械臂非高速运转时,忽略关节间的哥氏力、离心力,以及与其他关节之间的耦合力矩。只有当机械臂高速运动时,向心力和哥氏力才是重要的。因为本机械臂的转动速度很低,故本文可不考虑哥氏力、离心力的影响。
令连杆1、2的质量分别为m1,m2。为简化分析,设杆件质心在杆件几何中心处,如图7所示。
由机械臂的几何关系可确定

式中:v1,v2分别为机械臂大、小臂质心线速度。

图7 机械臂杆件动力学分析Fig.7 Arm dynamics analysis
系统动能Ek= ∑Eki,i=1,2,且

式中:m1,m2分别为机械臂大、小臂质量。
拉格朗日算子

拉格朗日方程

式中:Ti为关节驱动力矩;qi为广义关节变量,此处为θi;j=1,2,…,n。
为求动力学方程,需先对拉格朗日算子进行微分,

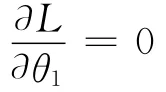
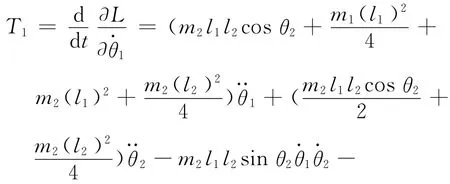

同理有

则关节2上的力矩为

采用拉格朗日方程分析了机械臂关节所受力矩情况,得到了关节力矩与运动学参数之间的关系,从而将运动学和动力学有机结合。
5 结束语
本文根据非合作目标卫星对接机构要求及特点,设计了一套非合作目标卫星对接机构,并通过ADAMS进行了对接仿真,仿真结果与理论分析较吻合,从原理上验证了对接机构设计的正确性。用D-H矩阵法分析了对接机构的正运动学和逆运动学问题,建立了末端执行器的位姿与关节变量的关系。用拉格朗日方程分析了机械臂关节所受力矩,推导出关节力矩与运动学参数间的关系,使运动学和动力学有机结合,为机械臂的位置和速度控制奠定了基础。为非合作目标卫星对接机构设计的后续工作提供了可靠依据。
[1] CASWELL D,VISENTIN G,ORTEGA G.ConeX-press orbital life extension vehicle-a commercial service for communications satellites[J].ESA Bulletin,2006,127:54-61.
[2] 蔡洪亮,高永明,邴启军,等.国外空间非合作目标抓捕系统研究现状与关键技术分析[J].装备指挥技术学院学报,2010,21(6):71-77.
[3] 张崇峰.空间对接机构综述[J].世界科学,2003(1):26-27.
[4] CURA D,MANUEL J.ConeXpress orbital life extension vehicle[C]// GNC 6th International ESA Conference on Guidance,Navigation and Control Systems.Loutrak:ESA,2005:1-2.
[5] 林来兴.美国“轨道快车”计划中的自主空间交会对接技术[J].国际太空,2005(2):23-27.
[6] WINGO D R.Orbital recovery’s responsive commercial space tug for life extension missions[R].AIAA,2004-6118.
[7] 梁 斌,徐文福,李 成,等.地球静止轨道在轨服务技术研究现状与发展趋势[J].宇航学报,2010,31(1):1-13.
[8] HKORTE J J,HODGE J S.Flow quality of hypersonic wind-tunnel nozzles designed using computational fluid dynamics[J].Journal of Spacecraft and Rockets,1995,32:569-580.
[9] HOFFMAN J.Design of compressed truncated perfect nozzles[J].Propulsion,1995,3(2):150.
[10] 张力平,马书根,李 斌,等.可重构星球探测机器人的运动学建模及轨迹规划[J].西安交通大学学报,2001,39(1):87-89.
[11] 黄献龙,梁 斌,陈建新,等.EMR系统机器人工作空间与灵活性的分析[J].机械工程学报,2001,37(2):14-15.
[12] DIAO Xiu-min,MA Ou,PAZ R.Study of 6-DOF cable robots for potential application of HIL microgravity contact-dynamics simulation[R]. AIAA,2006-6732.
[13] 赵红伟.斜四关节手腕运动与动力学分析及仿真研究[D].哈尔滨:哈尔滨工业大学,2006.
