由幂函数生成的广义李萨如图形
2015-12-30李京颍王春晓
李京颍,王春晓
(阜阳师范学院 物理与电子工程学院,阜阳 236037)
由幂函数生成的广义李萨如图形
李京颍,王春晓
(阜阳师范学院 物理与电子工程学院,阜阳 236037)
基于拓扑分析,将标准李萨如图形的两个分运动方式由简谐函数推广到半波对称函数,得到了一类与标准李萨如图形拓扑等价,但更一般的周期平面曲线。构造出了与正弦函数拓扑等价的半波对称连续函数,给出了完成上述方案的具体程序。用科学计算软件Mathematica得到了由各种不同的幂函数生成的广义的李萨如图形,并给出了它们的统一规律。最后讨论了广义李萨如图形的对称性,给出了相应的判别条件。
幂函数;李萨如图形;Mathematica
李萨如图形是两个互相垂直的简谐运动在频率比为有理数时生成的几何曲线[1],具有稳定的封闭的运动轨迹。李萨如图形在电学、光学、声学等领域中有着广泛的应用[2-4]。在工程技术领域,人们常常利用李萨如图形来测量分振动的频率和确定相位差。近年来,人们对李萨如图形进行了较为深入和广泛的研究,文献[5]研究了李萨如结,即高维的李萨如图形,并将构成李萨如图形的分运动推广到较为一般的周期运动,可以用有限项的傅里叶级数来描述;文献[6]从量子力学的角度研究了形成李萨如图形的物理学机制,并讨论了经典的周期曲线与量子系统简并度之间的联系。本文的目的是在保证拓扑等价的情况下,将构成标准李萨如图形的分运动推广到更为一般的情况。
按文献[7],简谐运动(以正弦函数为例)只是一种特殊的半波对称函数。一般地,由单调增函数生成的连续半波对称函数与正弦函数拓扑等价,形成一个拓扑等价类。我们将通常标准李萨如图形的分振动形式由简谐运动改为拓扑等价的连续半波对称函数,可以得到与经典李萨如图形拓扑等价
的更一般的平面周期曲线,即广义李萨如图形。作为典型的例子,我们给出了一类由幂函数生成的广义李萨如图形。
1 正弦函数的拓扑等价类
不失一般性,我们考虑正弦函数形式的简谐振动。容易验证,以T为周期的正弦函数
f(x)=sin(2πx/T)
(1)
具有如下性质:

2)在原点处连续,关于原点对称;
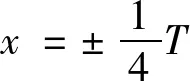
显然,具有上述性质的连续周期函数都与正弦函数拓扑等价,形成一个拓扑等价类。

(2)
按照文献[7],这样构造出来的函数与简谐函数具有同样的增减性,是一个半波对称的连续函数。
与上述定义对应的Mathematica命令[8]为
F[x_]:=f[x]/;x<=T/4;F[x_]:=f[T/2-x]/;x<=T/2;F[x_]:=-F[x-T/2]/;x<=T;F[x_]:=F[x-T]/;x>T
例如,我们取线性函数f(x)=x,T=4,由上述Mathematica命令可以得到
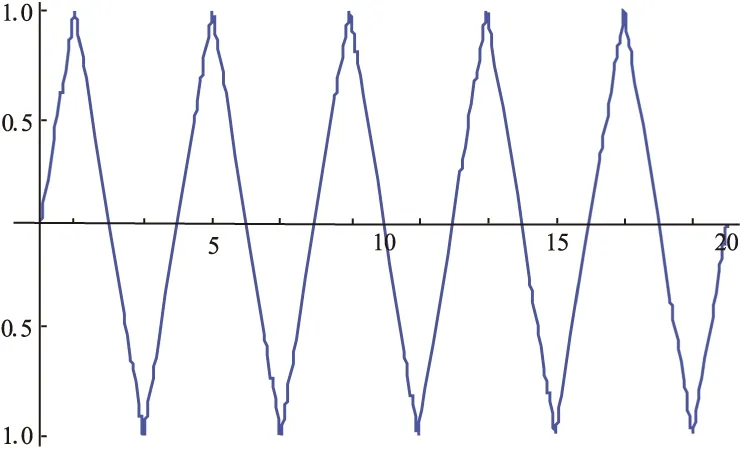
图1 由线性函数生成的半波对称连续函数
这正是我们所熟悉的三角波图形。

其中取非线性函数为f(x)=x2,完整的Mathematica程序如下:
f[x_]=x^2;T=4;
F[x_]:=f[x]/;x<=T/4;F[x_]:=f[T/2-x]/;x<=T/2;F[x_]:=-F[x-T/2]/;x<=T;F[x_]:=F[x-T]/;x>T
Plot[F[x],{x,0,20}]
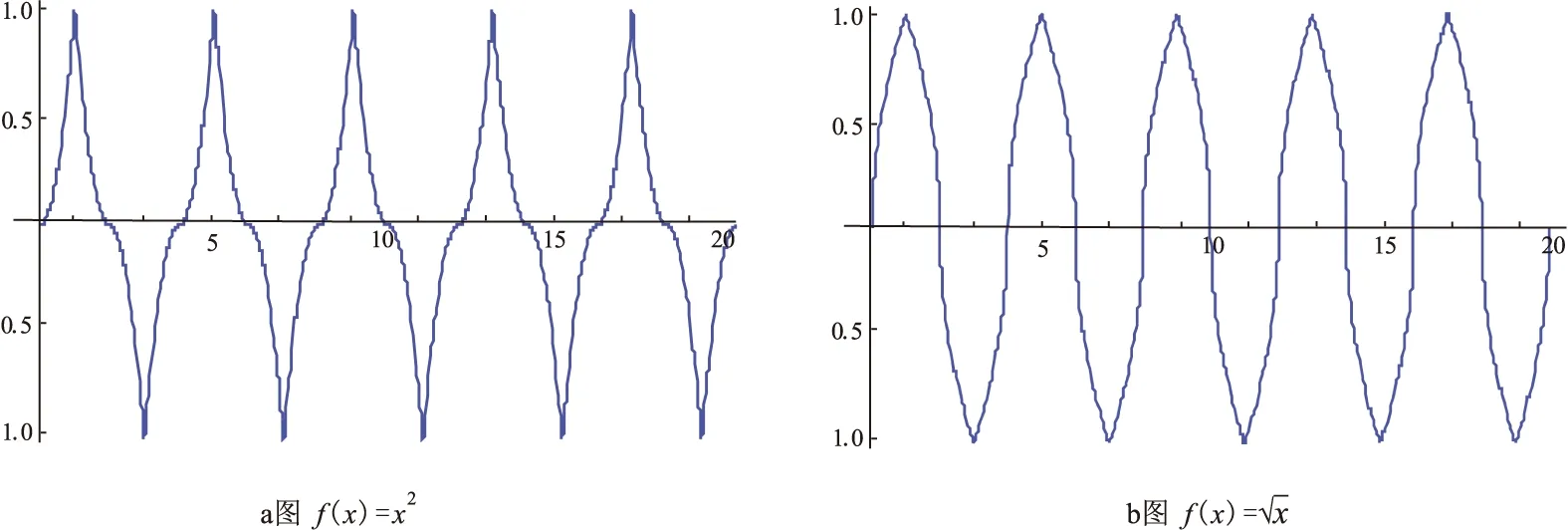
图2 由非线性函数生成的半波对称连续函数
f[x_]=x^(1/2);T=4;
F[x_]:=f[x]/;x<=T/4;F[x_]:=f[T/2-x]/;x<=T/2;F[x_]:=-F[x-T/2]/;x<=T;F[x_]:=F[x-T]/;x>T
Plot[F[x],{x,0,20}]
按照这样的方法,可以由任意的单调连续函数构造出与正弦函数拓扑等价的半波对称连续函数。
2 广义李萨如图形
标准李萨如图形的参数方程为
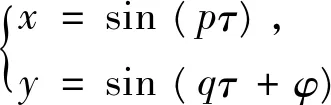
(3)
其中p,q为正整数,而φ为两个相互垂直简谐振动分量的位相差。
按照上面的方案,我们可以将标准李萨如图形中的正弦函数改为其拓扑等价类中的任意一个函数,所生成的图形与标准李萨如图形拓扑等价,可以认为是广义的李萨如图形。
为了具体起见,我们考虑由幂函数生成的半波对称函数,以此构造出广义的李萨如图形。
2.1 部分广义李萨如图形
先保持X方向的振动周期为T= 2π/p的正弦波,将Y轴方向的振动变为周期为T= 2π/q的半波对称函数。即
(4)
由此可以构造出部分广义李萨如图形。
为了简单起见,我们取位相差为φ= π/2,
q=1,利用Mathematica软件作图,得到结果如下:
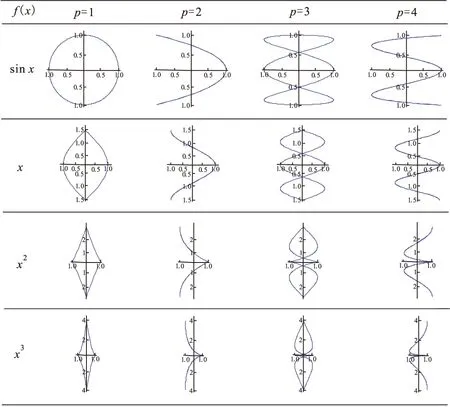
图3 广义李萨如图形与标准李萨如图形的对比
上表中第一行为标准的李萨如图形,可以用来进行比较。
2.2 完全广义李萨如图形
现在我们考虑X、Y方向的振动都是半波对称函数的情况,即
(5)
容易检验,所得图形与标准李萨如图形拓扑等价。
更一般地,我们还可以在X、Y方向分别取不同的半波对称函数。
2.3 对称性
下面以完全广义李萨如图形为例,对其对称性进行研究。
根据(5)式,当t=t1和t=t2时,分别有
要使y2=-y1,则
(6)
把(6)式代入x2得

此时要使x2=x1,则得到
pt2=pt1+2mπ,

图4 不同位相差和频率比的广义李萨如图形
即广义李萨如图形关于y轴对称,要满足条件
p(2k+1)=2mq
(7)
其中m,k为任意整数。
在满足y2=-y1,还满足x2=-x1,即广义李萨如图形关于原点对称,要满足条件

整理得
(8)
其中m,k为任意整数。
3 结论
本文将生成李萨如图形的简谐函数推广到了与其拓扑等价的半波对称函数,由此构造出了非常一般的广义李萨如图形。利用科学计算软件Mathematica具体给出了由幂函数生成的广义李萨如图形,这些新得到的图形与标准的李萨如图形拓扑等价,可以认为是标准的李萨如图形的一种具有普遍性的推广。
[1] 黄时中,倪致祥.大学物理(上册) [M].北京:高等教育出版社,2014:115-120.
[2] 张玉莲,宋双杰.李萨如图形在检测系统中的应用[J].力学与实践,2006,28(5):54-57.
[3] 梁 生,盛新志,娄淑琴,等.基于Lissajous图形的光纤分布式扰动传感器定位方法[J].红外与激光工程,2013,42(7):1896-1901.
[4] 郝艳捧,王晓蕾,阳 林.基于Lissajous图形研究大气压氦气介质阻挡放电[J].电工技术学报,2009,24(7):11-15.
[5]BoocherA,DaigleJ,J.Hoste&W.zheng.samplinglissajousandfourierknots[J].J.Experiment.Math, 2009, 18(4): 481-497.
[6]LauritzenB.Discretesymmetriesandtheperiodic-orbitexpansions[J].PhysicalReview.A1991,43:603-606.
[7] 郑君里,应启珩,杨为理.上册[M].2版.北京:高等教育出版社,2000:94-97.
[8] 倪致祥.科研的有力工具——Mathematica[J].阜阳师范学院学报(自然科学版),2005,22(2):7-10.
ExtendedLissajous'figuresgeneratedbythepowerfunctions
LIJing-ying,WANGChun-xiao
(SchoolofPhysicsandElectronicEngineering,FuyangNormalUniversity,FuyangAnhui236037,China)
Basedonthetopologicalmethod,thestandardLissajous'figuresgeneratedbythesimpleharmonicfunctionswasextendtoaseriesofnewresultsgeneratedbythehalfwavesymmetricfunctions,andtheextendedLissajous'figuresareequivalenttothestandardonesinthetopologicalproperties.Inaddition,aclassofnewLissajous'figuresgeneratedbythepowerfunctionsusingtheMathematicawasobtained,andanunitelawforthemwasgiven.Atlast,thesymmetryofextendedLissajous'figureswasdiscussed,andthecorrespondingdiscriminantconditionswasgiven.
powerfunctions;Lissajous'figures;Mathematica
2015-07-25
国家自然科学基金项目(11273008);安徽省教学团队项目(20100636);阜阳师范学院教学研究项目(2010JYXM37,2015JYXM34)资助。
李京颍( 1962-) ,女,学士,副教授,研究方向:计算物理、物理教育。
O321
A
1004-4329(2015)04-034-04
10.14096/j.cnki.cn34-1069/n/1004-4329(2015)04-034-04
