重力流长距离输水工程经济直径分析计算

高仁超，李 玥

（辽宁省水利水电勘测设计研究院，辽宁沈阳110006）

重力流长距离输水工程经济直径分析计算

高仁超，李 玥

（辽宁省水利水电勘测设计研究院，辽宁沈阳110006）

文章针对示例输水工程的经济洞径（管径）确定进行了探讨。根据工程的实际情况，对不同隧洞直径与管道内径的组合进行比较，并合理分配各段水力损失。在此基础上，最终确定了最佳的洞径与管径组合，使工程总投资最小。

重力流；经济管径；经济洞径；综合造价

1 引言

经济洞径和经济管径的计算分析，旨在合理选择隧洞和管道的内径，确定某种组合，合理分配各段输水隧洞及管道在设计输水流量下的水力损失，在保证输水工程全程重力自流的情况下，使工程的静态总投资最小。

某示例输调水工程拟采用全程自流输水，即利用起点水库与终点水库之间的水位差，全程采用重力流输水。输水线路全长498.845km，中途共设5座配水站、1个分水闸和2个分水口。为保证输水安全和减少水量漏失，输水设施均由隧洞和管道组成的封闭系统输水。受地形地貌影响限制，隧洞总长190.632km，共16段；管线总长308.213km，共22段，输水系统由管道和隧洞共38段组成。

输水管线由2条至4条管道组成，输水均为满流，断面也均为圆形；而隧洞只有1条，有的为满流，有的为非满流，断面形式较为复杂。两种设施的水力损失计算有一定的差异，故将隧洞和管道分别考虑为宜。即，先按隧洞和管道进行总水头预分配，再求出在总水头分配组合下的隧洞最少投资和管道最少投资的总合。最后按不同的总水头预分配组合分别计算，隧洞和管道总投资最小的组合就是最优的总水头的分配方案。

2 输水管道经济管径分析计算

示例工程输水线路由多条等直径的管道组成，水力坡降相同，故在经济内径计算中只计算其中的一条即可。

输水流量一致却并不连续的各段输水管道，只要条数相同，经济直径的计算结果也一定相同。故将输水流量相同的管段合并为一长段计算。

管道沿程水头损失计算推导如下：

式中：V—管道流速（m/s）；

C—谢才系数；

R—水力半径（m）；

J—水力坡降（m/m）。

式中：n—管道糙率，所有管道均取0.0115。另取管线局部水头损失为总水头损失5%计，由公式（1）、（2）可推导管道水力计算公式：

式中：Ji—第i段管道的水力坡降；

qi—第i段管道的流量（m3/s）；

Di—第i段管道的内径（m）；

hi—第i段管道的水头损失（m）；

Li—第i段管道的长度（m）。

为了能够求取经济管径，须建立管道投资与管道内径关系的数学模型，以乘幂函数表达。

输水管道工程的造价除考虑管材及管件本身采购、运输、安装的单价之外，还应综合考虑其附属设备设施、交叉建筑物、移民占地等多种因素的综合造价。

单位长度管道综合造价见表1。

根据表1，将管道直径——造价曲线绘制如图1所示。

图1 管道直径～造价关系图

管道直径与造价的乘幂数学模型为

式中：C—管道综合造价（元/m）；

D—管道内径（m）；

a—本工程为2416；

b—本工程为1.423。

第i段管道的费用总值表达式如下：

式中：Wi—为第i段管道投资（元）；

K—为考虑折旧、大修等因素的定值

系数。

由（5）（6）（7）推导出下式

式中：W—为各段管道总投资（元）。

令K1=1.5625K a，则（8）式为

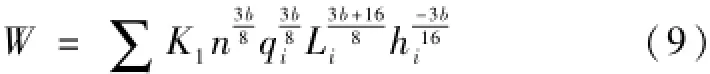
分析：最经济的管道直径就是（9）式中总投资W值最小。条件是总水头损失为定值。

利用拉格朗日乘数法求极值

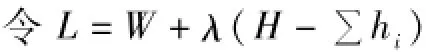
对hi求导

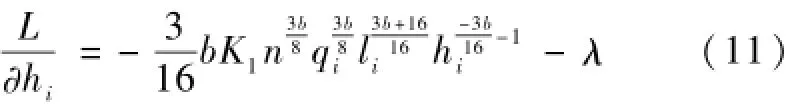
令上式等于0，得

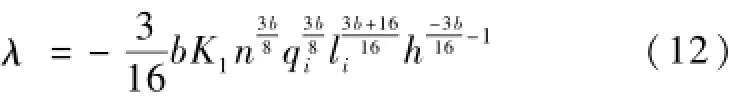
同理：

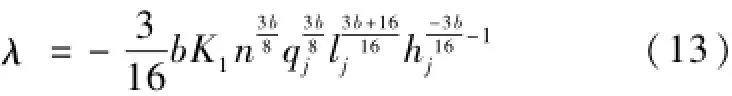
由（12）和（13）可进一步得出下式

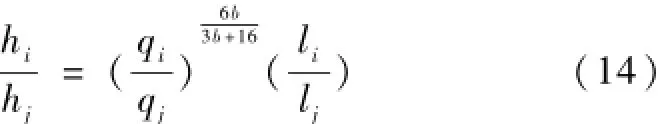
由（10）和（14）联立求解即可得各段管道直径。

当分配给管道总水头为83.6m时，管道综合造价计算成果见表2。

表1 管道工程单位长度综合造价表

表2 管道综合造价计算成果表

3 输水隧洞经济洞径分析计算

根据不同的水流条件、施工技术和运用要求，无压隧洞断面一般选取圆拱直墙或圆拱曲墙断面。但为了能够满足经济洞径的计算条件——即隧洞的过流量是洞径和坡降的函数，因此在经济洞径的计算中，无论是压力隧洞还是无压隧洞，隧洞断面均按圆形铺底断面考虑，待具体设计中，可以采用相近过流能力的其他更加合理的断面进行代替。

隧洞采用圆形铺底断面，铺底宽度B=隧洞内径R，洞顶空隙率取20%，过水断面的计算模型如图2。

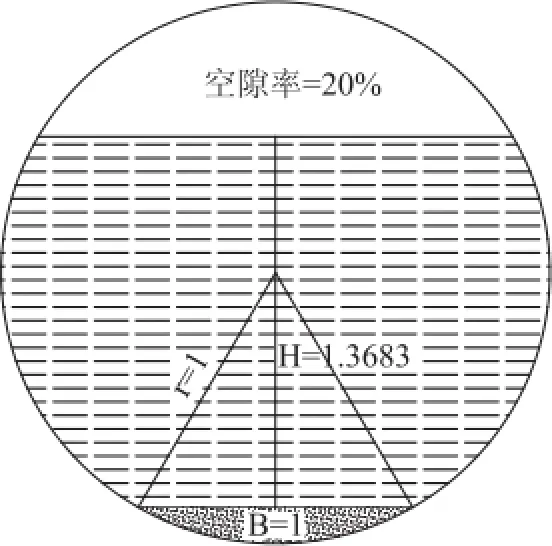
图2 输水隧洞过水断面计算模型

推导过程同管道的推导，隧洞水力计算公式如下：

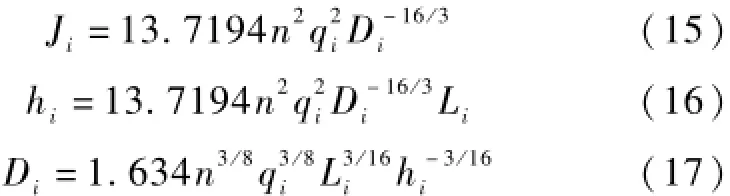
式中：Ji—第i段隧洞的水力坡降；

qi—第i段隧洞的流量（m3/s）；

Di—第i段隧洞的内径（m）；

hi—第i段隧洞的水头损失（m）；

Li—第i段隧洞的长度（m）。

为了满足经济洞径计算的要求，隧洞全程的围岩类型分段做围岩比例分析，并计算各类围岩占长度的加权平均值。取值结果见表3。在综合考虑施工方法、建设条件、支洞布置、工程占地、道路交通、弃渣处理等因素后，单位长度隧洞综合造价见表4。

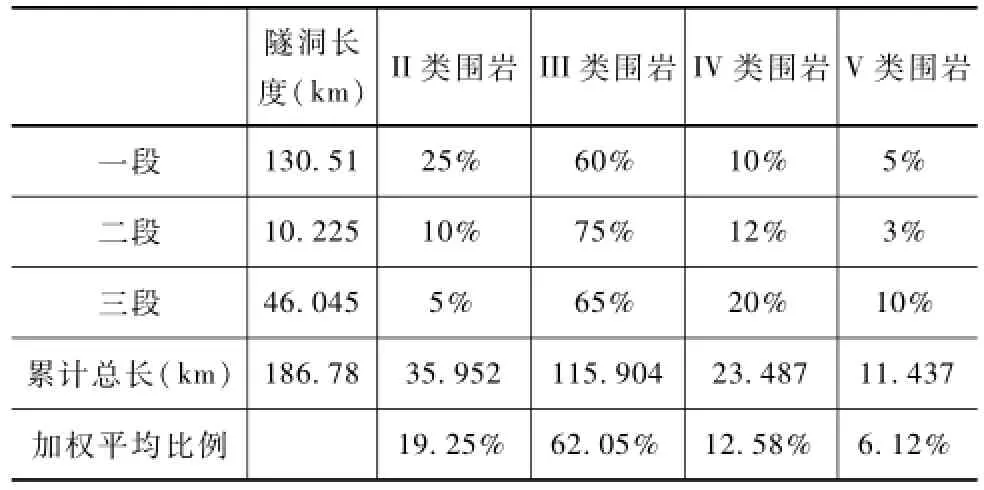
表3 隧洞围岩分类比例表

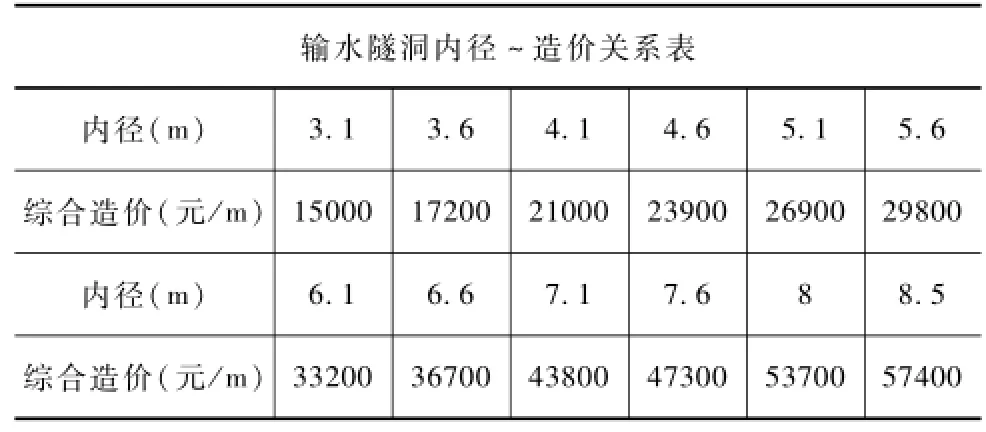
表4 隧洞工程单位长度综合造价表

根据上表，将隧洞内径——综合造价曲线绘制如图3所示。

图3 隧洞内径～造价曲线图

建立隧洞直径与造价的乘幂数学模型

式中：C—管道综合造价（元/m）；

a—本工程为3114.0；

b—本工程为1.3396。

同管道经济内径推导过程（从略），在总水头损失确定的情况下，各段隧洞间满足下式关系时，隧洞总投资最少。

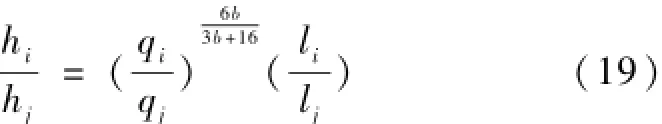
当分配给隧洞总水头为48.4m时，隧洞综合造价计算成果见表5。

表5 隧洞综合造价计算成果表

4 经济洞径和经济管径分析计算

示例工程采用全程重力自流，输水线路的总水头损失为139.4m，合理分配各段隧洞、管道的水力损失，使工程总投资最低的方案，就是最经济的方案。由于输水管道和隧洞的内径——造价关系函数不同，故无法直接计算极值，下面通过试算的方法，分别试算管道和隧洞在不同分配水头情况下的经济内径和总投资，再将两者合计，之极小合值就是最优组合。具体比较数值见表6。

表6 隧洞和管道不同分配水头综合造价比较表

输水管道分配水头—工程总投资曲线见图4。

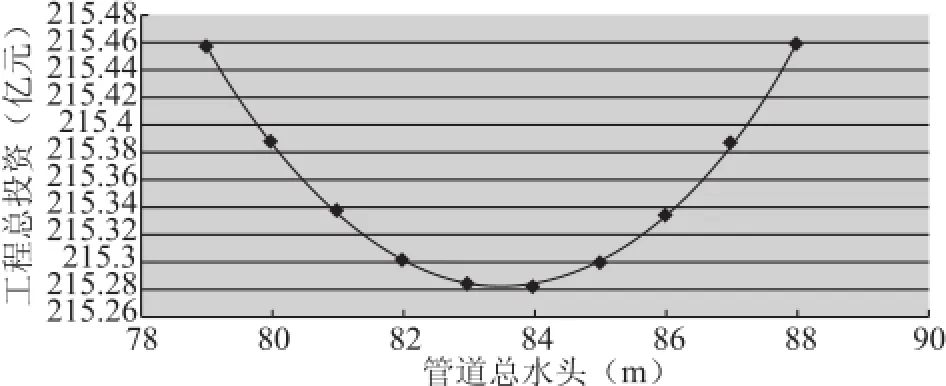
图4 工程总投资与管道总水头关系曲线

从图4可以看出，当管道分配水头83.6m、隧洞分配水头48.4m时，总投资为215.281亿元，为最优组合。

按上述水头分配的情况，再分别计算输水管道的经济管径和输水隧洞的经济洞径，根据各段工程所处的地理、地形、地质和管理等因素，采用适宜的结构和断面形式，分别优化，最终确定工程的实际管径、洞径，如表7、表8所示：

表7 各段输水管道经济直径计算成果表

5 结论

通过上述示例工程设计实例，针对全程重力流输水工程，采用建立适当的数学模型计算确定了最优的管径和洞径组合。即在总水头确定的情况下，通过数学方法对管道和隧洞进行合理的水头分配，推求出了工程总投资最小的管径和洞径。

T V 672

B

1672-2469（2015）06-0087-04

10.3969/j.i s s n.1672-2469.2015.06.030

高仁超（1972年—），男，高级工程师。