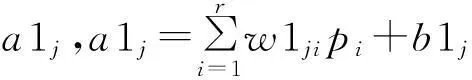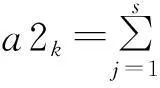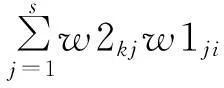配电网电压暂降状态估计单层神经网络法
2015-12-30李国栋吕金炳
汪 颖,唐 琳,李国栋,林 芳,吕金炳
(1.四川大学电气信息学院,四川 成都 610065;
2.国网天津市电力公司电力科学研究院,天津 300384)
配电网电压暂降状态估计单层神经网络法
汪颖1,唐琳1,李国栋2,林芳1,吕金炳2
(1.四川大学电气信息学院,四川 成都610065;
2.国网天津市电力公司电力科学研究院,天津300384)
摘要:应用单层线性神经网络求解电压暂降状态估计问题。对比单层线性神经网络和多层线性神经网络的结构和输入输出特性,并使用Matlab神经网络工具箱对IEEE 30节点可靠性测试系统进行仿真,证明两种网络有相同功能,能达到相同误差精度。但单层线性神经网络结构更简单,能大幅提升计算速度。
关键词:电压暂降;状态估计;区域电网;单层线性神经网络
0引言
电压暂降状态估计(voltage sag state estimation,VSSE)是利用系统内有限监测点的暂降频次信息和状态估计方程估计其余节点的暂降频次。实际中由于监测点数量有限,状态估计方程是高欠定方程[1],其求解算法是值得研究的重要课题。
状态估计欠定线性方程的求解,现已有的整数线性规划法[1]、遗传算法[2]、bp神经网络[3]等,均存在计算时间过长的问题。bp网络含多层神经元,结构复杂,导致计算时间增加;bp网络隐层神经元数的确定目前还没有统一的方法,都是依靠经验选取,通常设计bp网络都用较高的结构冗余性满足较低的精度要求,造成计算时间大幅增加。
根据VSSE方程的线性特点,选择单层线性神经网络,该网络结构简单只含一层神经元,极大精简了神经网络结构,去除冗余部分神经元。因此,单层线性神经网络求解VSSE方程能在保证精度的同时,大幅减少计算时间。
将单层线性神经网络和多层线性的bp神经网络的结构和输入输出特性做对比,从理论上证明两者拥有相同的传递功能,但单层线性网络结构更简单;用IEEE 30节点可靠性测试系统进行仿真测试,从仿真中证明两者能达到相同精度,但单层线性网络速度更快,更具优越性:因此,在求解VSSE欠定线性方程上,单层线性神经网络完全可以取代bp神经网络。
1电压暂降方程
状态估计通用的数学方程式如下[1]:
H=MX+E
(1)
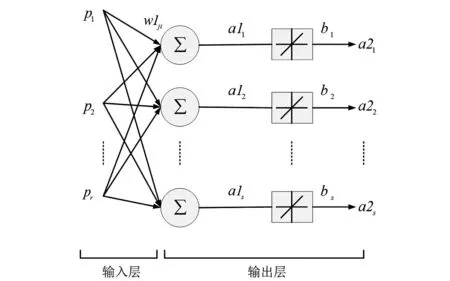
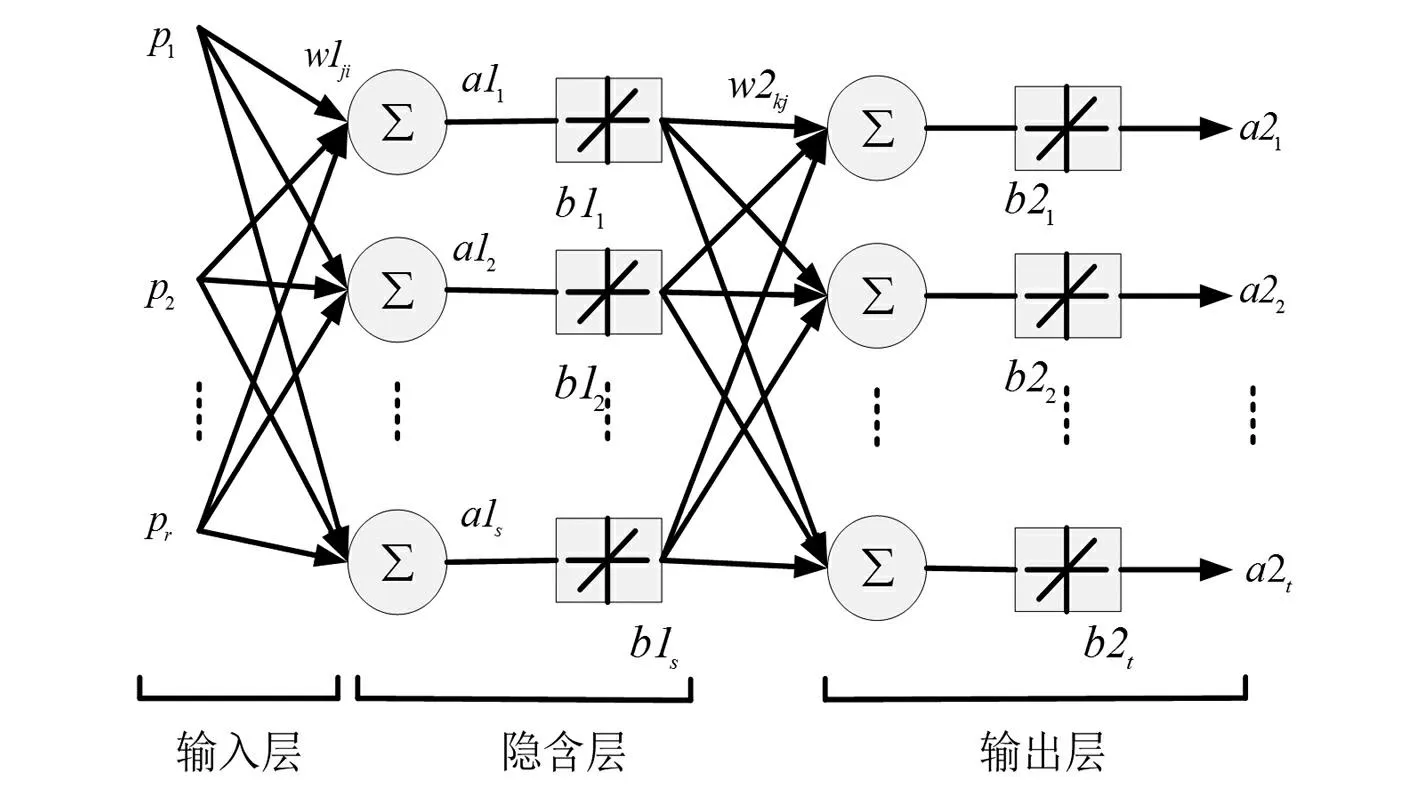
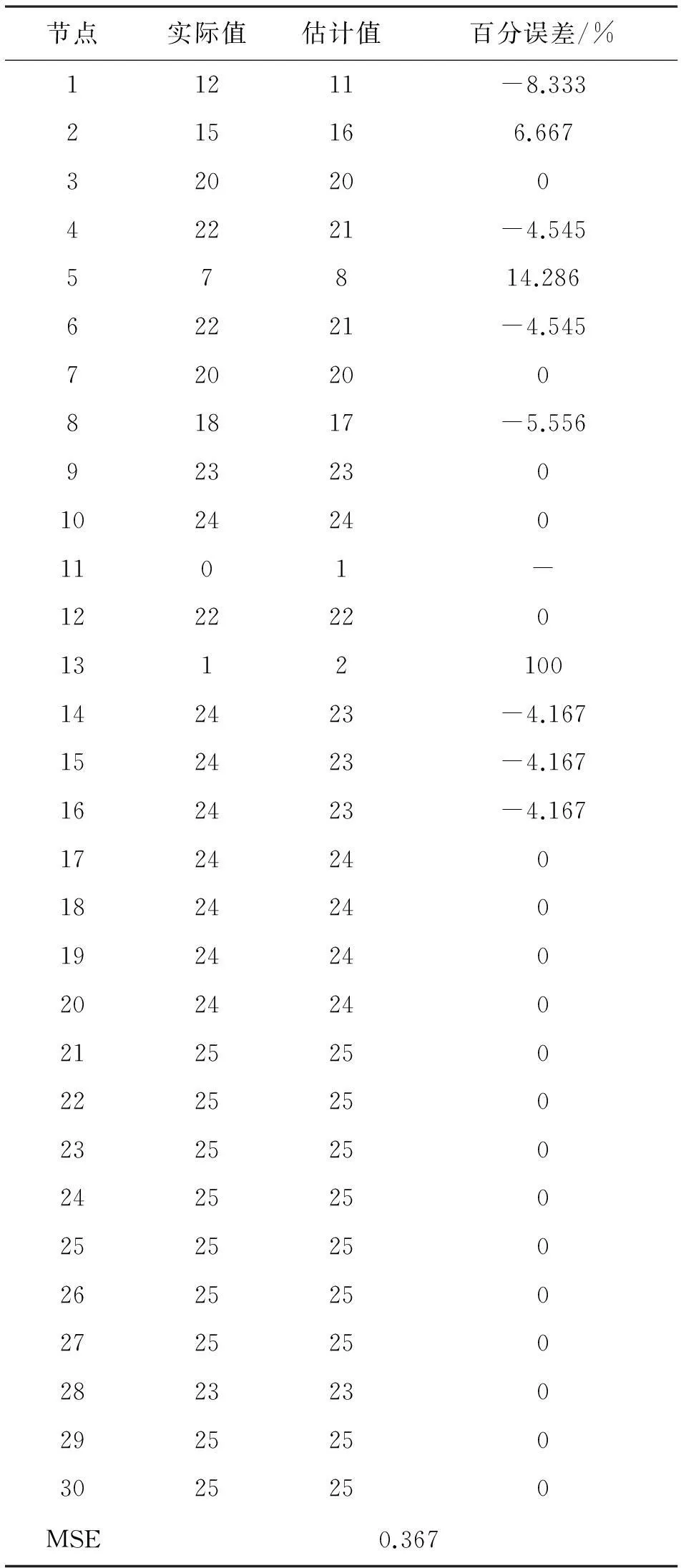
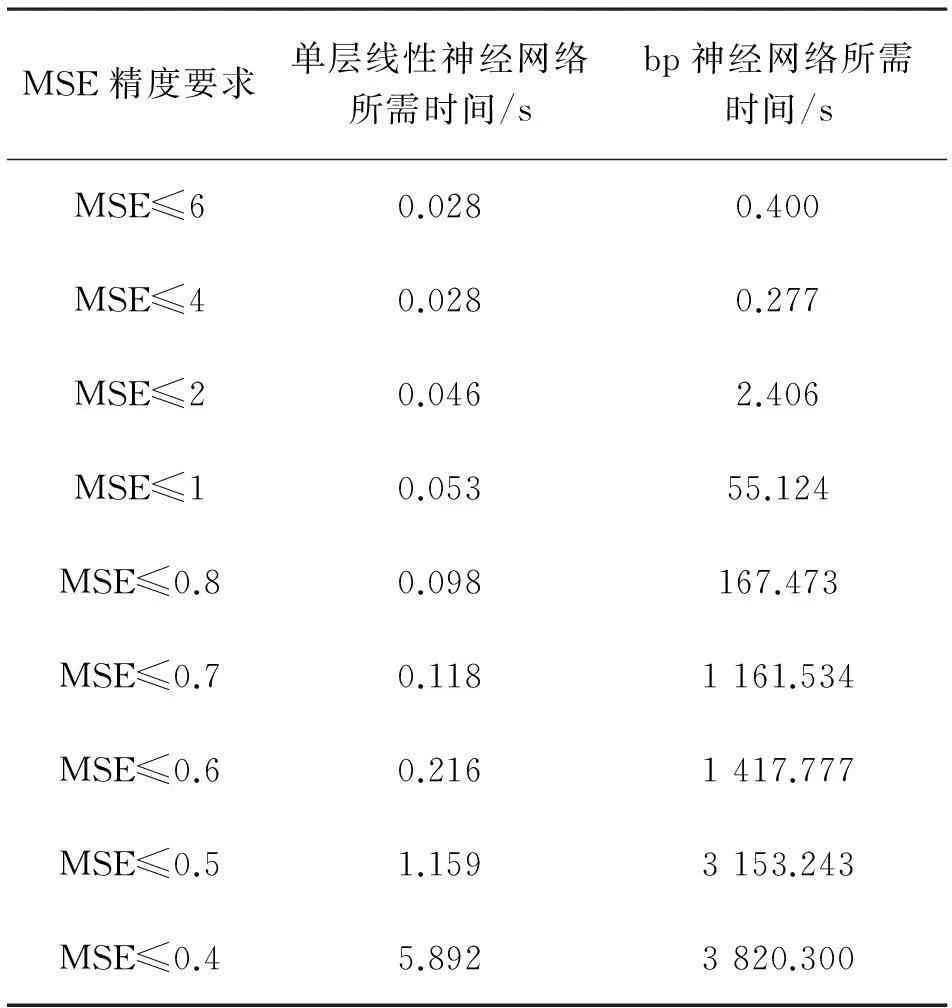
式中,H表示测量向量;X是待估计的状态向量;M是测量矩阵;E向量代表测量噪声,在VSSE中,该向量被忽略[4]。任意的一个电力系统,假设有N个节点,L条线路和M个监测点,在该问题中M 对于设定的电压暂降阈值t1,式(1)在VSSE应用中的具体含义如下: 1) 测量向量H1:测量向量H1表示所有监测点监测到的剩余电压≤设定电压阈值t1的电压暂降频次。它是从安装监测装置的M个监测点直接获取的,能构成M行的向量H1。 2)状态变量X:向量X由待估计的状态变量组成。其中每一个变量表示在对应线路分段上发生故障的次数。线路故障分段的概念和具体方法见文献[1]。相同线路分段上发生多次故障,对同一个母线节点是否发生暂降的影响是相同的。如果总的线路分为P段,则X向量为P维。 3)测量矩阵M1:测量矩阵M1是(M×P)维的0-1矩阵。对于任意的一个元素m1(mi,pi),若对应故障分段pi上发生的故障,会导致节点mi的剩余电压低于阈值t从而导致暂降,则取值为1;反之,如果该故障不会导致暂降,则该元素为0。 4)求解:式(1)是一个欠定线性方程,采用单层线性人工神经网络求解得到状态变量X的值,然后通过状态估计方程求取待估计节点的暂降频次。对于任意的非监测节点i,测量矩阵Mi和前面测量矩阵M1的求取方法相同,表征对应线路分段发生故障是否会导致非监测点i发生暂降。任意待估计非监测点的暂降频次hi的表达式为 (2) 考虑多种暂降阈值和多种故障类型的VSSE方程拓展见文献[1]。 2单层线性神经网络和bp神经网络在该问题中的对比 应用线性神经网络对VSSE方程进行求解,可以设计简单的单层线性神经网络(newlind),或者利用bp神经网络的创建函数(newff)设计含有一个(或以上)隐层的多层线性神经网络,参见文献[3]。下面证明单层线性神经网络和bp设计的多层线性神经网络具有相同的输入输出特性。 如图 1所示是具有r个输入s个输出的单层线性神经网络模型,在该网络中,全部神经元都选线性传递函数。其中,[p1,p2,…,pr]T是输入向量,偏差和权重如图1中所示,输入层的输出为a1j[5]: (3) 输出层的输出为a2j: (4) 以含有一个隐层的两层线性神经网络为例,其输入向量仍是r维,所有的神经元都选线性传递函数。 图1 单层线性神经网络结构 图2 多层线性神经网络结构 (5) 式中,i∈[1,r],j∈[1,s],k∈[1,t]。 (6) 那么,公式(5)可以写成式(7): (7) 所以,含有一个隐层的多层线性网络的的输入输出关系可以用式(7)表示。把式(4)与式(7)比较,发现它们在形式上是相同的,只是多层线性网络比单层线性网络具有更复杂的权重和阈值。因此两者具有相同的能力。但多层网络结构更为复杂,计算时间也更长,所以多层线性网络完全可以被单层线性网络所替代[5]。使用神经网络方法求解VSSE方程H=MX,应用单层线性网络就已经足够。该方法能在保证精度的情况下,大幅提升计算速度。 3单层线性网络求解VSSE方程 神经网络训练数据需要输入和对应的标准输出。对于式(1),把H作为输入,而X作为输出。 用蒙特卡洛法[6]生成故障点,这些故障点包括任意的故障类型,可以落在系统内所有线路的任意位置上。随机生成选定次数的故障后,统计每个线路分段内的故障次数,即是生成了一组状态变量X,由于测量矩阵M已知,根据方程(1)就可以求到对应的测量向量H,从而生成了一组训练数据H和X。如此重复n次,则得到n组训练数据。 利用Matlab神经网络工具箱的newlind函数,建立自适应的单层线性神经网络模型,对输入H和输出X进行训练,得到网络net。将实际监测到的一组H作为测试数据输入,经过net可以得到单层线性神经网络给出的状态变量X的结果。再根据方程(2)可得任意节点的电压暂降频次估计值。 4案例仿真 将所提方法应用于IEEE 30系统进行仿真,该系统有30个节点,37条线路[7],根据[8]的方法,选定0.9 p.u.阈值下的监测点为7、24共2个,系统结构如图3。在此监测装置配置情况下对发生的0.9 p.u.电压暂降进行估计。 表1是应用单层线性神经网络在0.9 p.u.阈值下的计算结果和误差。其中,MSE(mean square error)均方误差表征估计值相对实际值的误差大小。表1中,电压暂降估计值与实际值误差很小,说明线性神经网络能很好地应用于VSSE问题,证明了所提方法的可行性和准确性。 表1 单层线性神经网络计算结果 图3 IEEE 30节点系统结构图 表2是在达到给定精度要求的条件下,两种神经网络所需计算时间对比。 表2 相同精度要求下两种神经网络计算时间对比 从表2可以看出,在达到相同等级的误差精度情况下,单层线性神经网络比bp神经网络所需要的时间更短,而且随着精度的提高,计算速度上的优势明显增大。综上说明,单层线性神经网络比bp神经网络更简单快速,能大幅提升计算速度,更适用于VSSE计算。 5结论 由于VSSE方程是欠定线性方程,采用单层线性神经网络和bp神经网络都可求解,但bp神经网络设计的多层线性网络结构复杂且具有高度冗余性,而单层线性神经网络结构更为精简,相同功能下选择结构简单的单层线性网络更为合适。应用单层线性神经网络求解VSSE方程,能在保证精度的同时大幅提升计算速度。在VSSE问题上,单层线性神经网络优于bp神经网络,更能满足工程实际的需要。 参考文献 [1]E. Espinosa-Juárez, A. Hernández. A Method for Voltage Sags State Estimation in Power Systems[J]. IEEE Transactions on Power Delivery,2007, 22(4):2517-2526. [2]J. Lucio,E. Espinosa-Jua′rez,A. Herna′ndez. Volta- ge Sag State Estimation in Power Systems by Applying Genetic Algorithms[J].IET Generation, Transmission and Distribution, 2011,5(2):223-230. [3]Elisa Espinosa-Juárez, EspinozaTinoco J R, Araceli Hernández. Neural Networks Applied to Solve the Voltage Sag State Estimation Problem: An Approach Based on the Fault Positions Concept[C]. 2009 Electronics, Robotics and Automotive Mechanics Conference, IEEE computer society, 2009:88-93. [4]Matair S S, Watson N R, Wong K P. Harmonic State Estimation: A Method for Remote Harmonic Assessment in a Deregulated Utility Network[C]. International Conference on Electric Utility Deregulation and Restructuring and Power Technologies 2000, City University, London, 2000:41-46. [5]崔小平. 几种前馈型神经网络分类性能的比较分析研究[D].太原: 中北大学, 2011:18-20. [6]刘晓娟, 肖湘宁, 陶顺. 基于EMTDC 电压暂降随机预估的仿真研究[J]. 现代电力, 2005, 22(5):13-17. [7]R. Christie. Power Flow Test Cases, 30 Bus Power Flow Test Case[EB/OL].1993[2013-8-20].http://www.ee.washington.edu/research/pstca/. [8]Olguin G, Vuinovich F, Bollen A M H J. An Optimal Monitoring Program for Obtaining Voltage Sag System Indexes[J]. IEEE Transactions on Power Delivery, 2006, 21(1):378-384. 中图分类号:TM74 文献标志码:A 文章编号:1003-6954(2015)04-0010-04 基金项目:高等学校博士学科点专项基金资助项目(20130181110004);国网天津市电力公司电力科学研究院项目 (收稿日期:2015-06-01) Abstract:Single layer linear neural network is used to solve the state estimation problems of voltage sag. The structure and input/output characteristics of single layer linear neural network are compared with that of multi-layer linear neural network, and the simulation of IEEE-30 bus reliability test system (RTS) is carried out by using Matlab neural network toolbox. The results demonstrate that these two kinds of networks have the same function, and can achieve the same error precision. But single layer linear neural network can significantly increase the computation speed because of its simpler structure. Key words:voltage sag; state estimation; regional power grid; single layer linear neural network2.1 单层线性神经网络
2.2 多层线性神经网络