一类二阶四元数方阵保左谱的线性映射表示*



一类二阶四元数方阵保左谱的线性映射表示*

袁庚

(青岛科技大学数理学院，山东青岛266061)

摘要：设Q表示四元数集合，Mn(Q)表示n×n四元数矩阵的集合.对于四元数右线性映射Φ(A)=UAU-1或Φ(A)=UATU-1： M2(Q)→M2(Q)，若σl[ Φ (A) ] =σl(A)，则四元数酉阵U是实数矩阵.

关键词：四元数方阵；保左谱；线性映射

引言

设R，C分别表示实数域与复数域，Q表示具有形式q=q0+ q1i + q2j + q3k∈Q的所有四元数集合，其中i2= j2= k2=-1，ij =-ji=k，jk =-kj=i，ki =-ik=j.对任意的q=q0+ q1i + q2j + q3k，=q0-q1i-q2j-q3k称为q的共轭，记为.

设K=R，C或Q，元素属于K的n×n阶矩阵的全体记为Mn(K).对于A∈Mn(Q)，用、AT、A*分别表示四元数矩阵A的共轭矩阵、转置矩阵、共轭转置矩阵.若A*= A则称A为四元数自共轭矩阵；若AA*= A*A=I，则称A为四元数酉矩阵.用Un(Q)表示n阶四元数酉阵的全体，SCn(Q)表示n阶四元数自共轭矩阵的全体，GLn(Q)表示n阶四元数可逆矩阵的全体，CM2(C)为所有元素为复数的2×2阶矩阵.

对于A∈Mn(Q)，若存在μ∈Q与n维非零列矢量X使得AX=Xμ，称μ为A的左特征值.称A的左特征值的集合为A的左谱，记为σl(A).

Wood［1］利用代数拓扑的方法证明四元数矩阵A∈Mn(Q)时，σl(A)是非空的，并且指出可以通过解二次方程来计算2×2阶四元数矩阵的左特征值.Huang和So［2］利用四元数二次方程给出了2×2阶四元数矩阵左特征值的计算过程，同时刻画了2×2阶四元数矩阵的左谱.Zhang［3］给出下面例子说明四元数矩阵的左谱不是相似不变的.

A∈Mn(Q)，α1，α2∈Q，ζ1，ζ2∈Qn，

A(α1ζ1+α2ζ2)=Aα1ζ1+ Aα2ζ2

一般不再成立.但是

A(ζ1+ζ2)=Aζ1+ Aζ2，ζ1，ζ2∈Qn； A(ζq)=(Aζ) q，ζ∈Qn，q∈Q

总是成立的，满足

A(ζ1+ζ2)=Aζ1+ Aζ2，ζ1，ζ2∈Qn与A(ζq)=(Aζ) q，ζ∈Qn，q∈Q

的矩阵A称为四元数的右线性映射.

在过去的30年里，很多作者讨论了线性保的问题以及线性保有关的问题，关于这方面的内容请参考文献［4～7］.注意到四元数矩阵A的左谱不是酉不变的，而四元数矩阵作为线性变换的运算也不同于实数域和复数域上矩阵的运算，本文主要讨论了一类四元数线性变换保左谱的具体形式.下面定理是本文的主要结果.

定理1设A∈M2(Q)，U∈U2(Q)，若四元数右线性映射Φ(A)=UAU*或Φ(A)=UATU*： M2(Q) →M2(Q)满足σl[ Φ (A) ] =σl(A)，则四元数酉阵U是实矩阵.

1　定理1的证明

1.1辅助引理

引理1[2 ]设，如果bc=0则σl(A) ={ a，d } ；如果bc≠0，则：

σl(A) ={ a + bλ：λ2+ b-1(a-d)λ-b-1b =0}

引理2[2 ]设，则σl(A)是无限的当且仅当bc≠0，b-1(a-d)∈R，b-1c∈R，且.特别的，如果σl(A)是无限的.

定义1 Φ： M2(Q)→M2(Q)称为四元数右线性映射，如果它满足：

引理3对于任意的A∈CM2(C)，U∈U2(Q)，若四元数右线性映射Φ(A)=UAU*满足σl[ Φ (A) ] =σl(A)，则U具有以下形式：

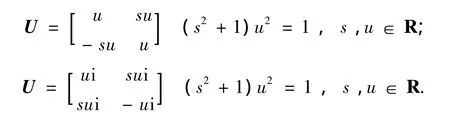
证明当满足命题条件且Φ(A)=UAU*时，确定U的表示.

因为U∈U2(Q)，设，由酉阵性质可得：

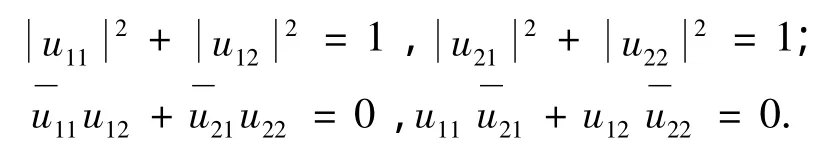
因为Φ(A)=UAU*，取，则：

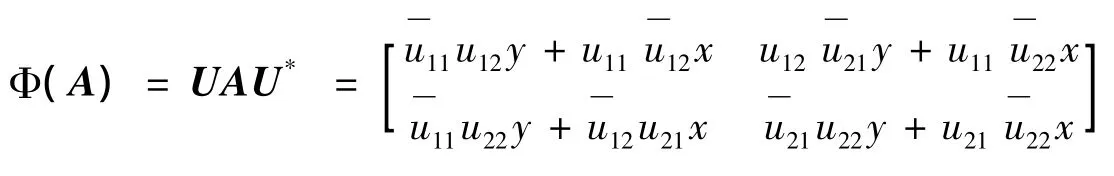
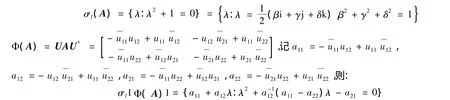
显然，σl(A)中的元素是无限的，由σl[ Φ(A)] =σl(A)，若方程有无限解，由引理2，则：

由a-112a21∈R且a21=-a12，a-112=∈R可以得到，即，从而a12∈R.又由，a12∈R，得到a11-a22∈R.

由酉阵性质可得：

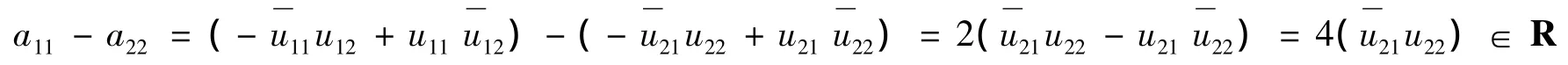
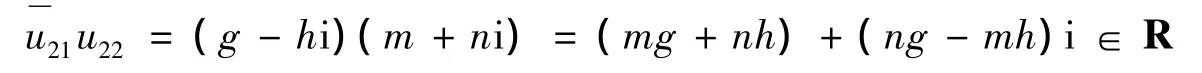
若假设s3= 0，则由s1+ s23s2= 0可以得到s1= 0，从而有，这与U是酉阵矛盾，假设不成立，舍去.

当s3≠0时，由s3(1 + s1s2)=0，得到1 + s1s2= 0；由s1+ s23s2= 0，得到s2s3=±1.

当s2s3= 1时，由s1+ s23s2= 0，得到s1=-s3，继而得到：

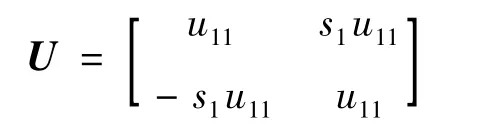
由U是酉阵，得到u211+ s21u211= 1，由1 + s21＞0得到u211＞0，即u11∈R，可以得到U的形式为：

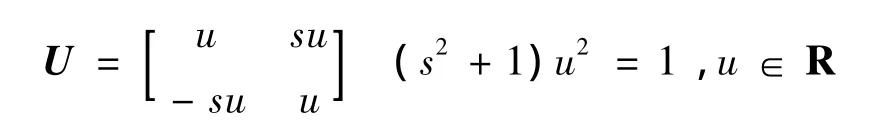
当s2s3=-1时，由s1+ s23s2= 0得到s1= s3，继而得到：

由U是酉阵，得到-u211-s21u211= 1，由1 + s21＞0，得u211＜0，继而得到U的形式为：

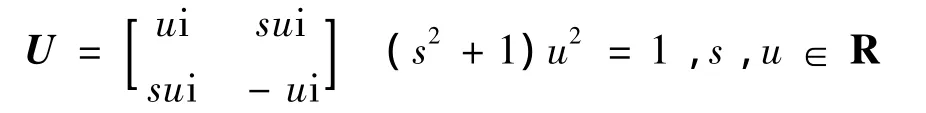
1.2定理1的证明

令A=A1+ A2j，A1，A2j∈C，由定义1可以得到：

Φ(A1+ A2j) =Φ(A1) +Φ(A2j) =Φ(A1) +Φ(A2) j

若σl[ Φ (A) ] =σl(A)，由引理3，则：

Φ(A1)=UA1U*；Φ(A2)=UA2U*

显然Φ(A2) j≠Φ(A2j)，舍去.

类似可证明Φ(A)=UATU*的情况.

2　结语

本文在M2(Q)→M2(Q)的条件下刻画了右线性映射Φ保左谱的具体形式，这个结果，有利于提高复杂四元数矩阵左谱的计算效率，同时也有益于更一般四元数矩阵左谱问题的研究.

参考文献：

［1］Wood R M W.Quaternionic eigenvalues［J］.Bull，London Math.Soc.，1985，17：137-138.

［2］Huang Liping，Wasin S.On Left Eigenvalues of a Quaternionic Matrix［J］.Linear Algebra and Its Application，2001，323：105-116.

［3］Zhang Fuzhen.Quaternions and Matrices of Quaternions［J］.Linear Algebra and its Applications，1997，251：21-57.

［4］Li C K，Tsing N K.Linear preserver problems： a brief introduction and some special techniques［J］.Lin.Alg.，1994，162-164： 217-235.

［5］Dokovic D Z，Li C.K，Overgroups of some classical linear groups with applications to linear preserver problems［J］.Lin，Alg.，1994，197-198：31-61.

［6］Guterman A，Li C K，Seml P.Some general techniques on linear preserver［J］.Lin.Alg.，2003，315：61-81.

［7］Li C K，Pierce S.Linear preserver problems［J］.Amer.Math.2001，108：591-605.

Linear Maps Preserving Left Spectrum of 2×2Quaternion Matrices

YUAN Geng

(Department of Mathematics，Qingdao University of Science and Technology，Qingdao 266042，China)

Abstract：Let Q be the set of quaternion numbers and Mn(Q) the set of n×n quaternion matrices.If quaternion right linear Maps Φ(A)=UAU-1or Φ(A)=UATU-1： M2(Q)→M2(Q) preserving Left Spectrum，then quaternion unitary matrix is real.

Key words：quaternion matrices； left spectrum； linear maps

作者简介：袁庚(1985-)，男，山东曹县人，在读硕士研究生，研究方向：代数学及其应用.

*收稿日期：2015-03-02

文章编号：1673-2103(2015) 02-0006-04

中图分类号：O151.24

文献标志码：A