幂级数部分和的组合表达式*
2015-12-09刘秀英
刘秀英
(菏泽学院数学系,山东菏泽 274015)
生成函数即母函数,是组合数学尤其是计数方面的一个重要理论和工具[1~6].生成函数可用来研究未知(通项)数列的规律,在给出递推公式的情况下求出数列的通项[7~10].另外,生成函数作为一类特殊函数 在函数论、解析数论、数学物理方程等学科的研究领域中也被广泛应用.本文以生成函数为工具,讨论了级数部分和的组合表达式,并讨论了由这些系数构成的三角形的对称性以及此三角形内相邻行间元素的递归关系.
1 引理
引理1.1[6]假设数列{an}的生成函数是A(t),则其部分和构成的数列{sn}的生成函数是其中,sn=a0+a1+…+an.
12+22+32+…+n2=
对k=3,需要下面的引理:
引理1.3[7]
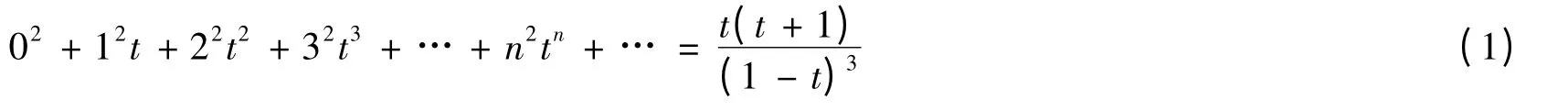
证明:对(1)式两边求导并整理得:

两边同乘以t,得
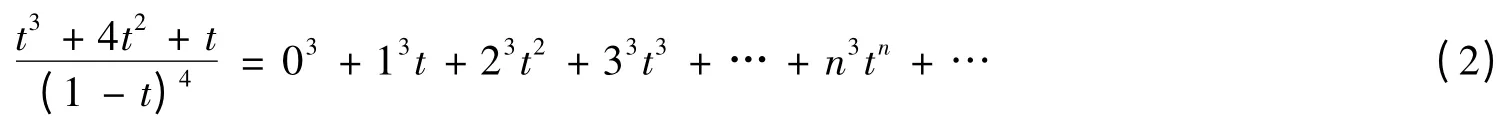
这样,数列 {03,03+13,03+13+23,…,03+13+23+…+n3,… }的生成函数为,即:
t3(1-t)-5+4t2(1-t)-5+t(1-t)-5
考虑(2)式中tn的系数,则有

引理4得证.
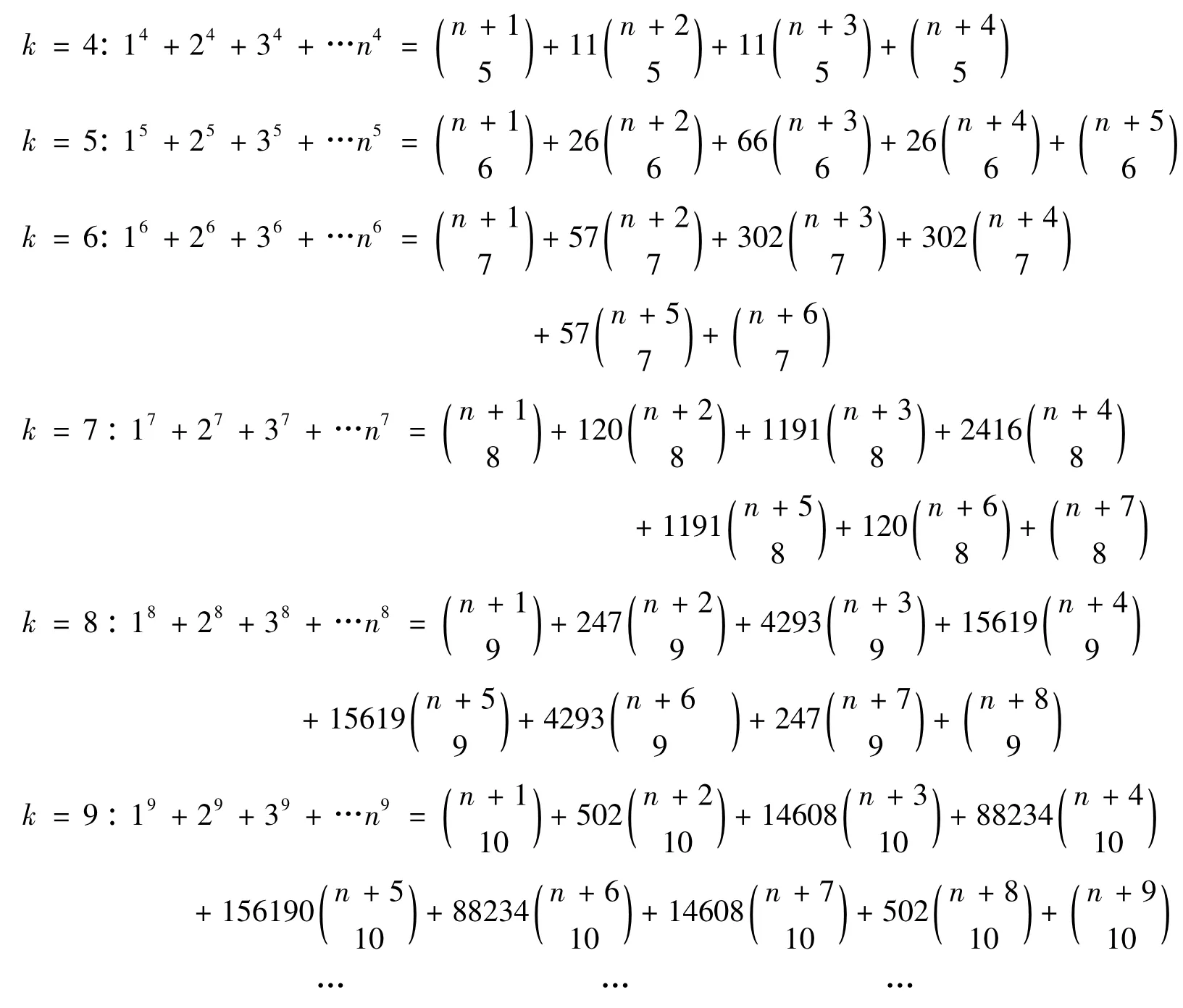
(i=1,2…k;k=1,2…):

表1
2 主要结论
由引理1.2和引理1.4~1.6,可以得出如下结论:
定理2.1
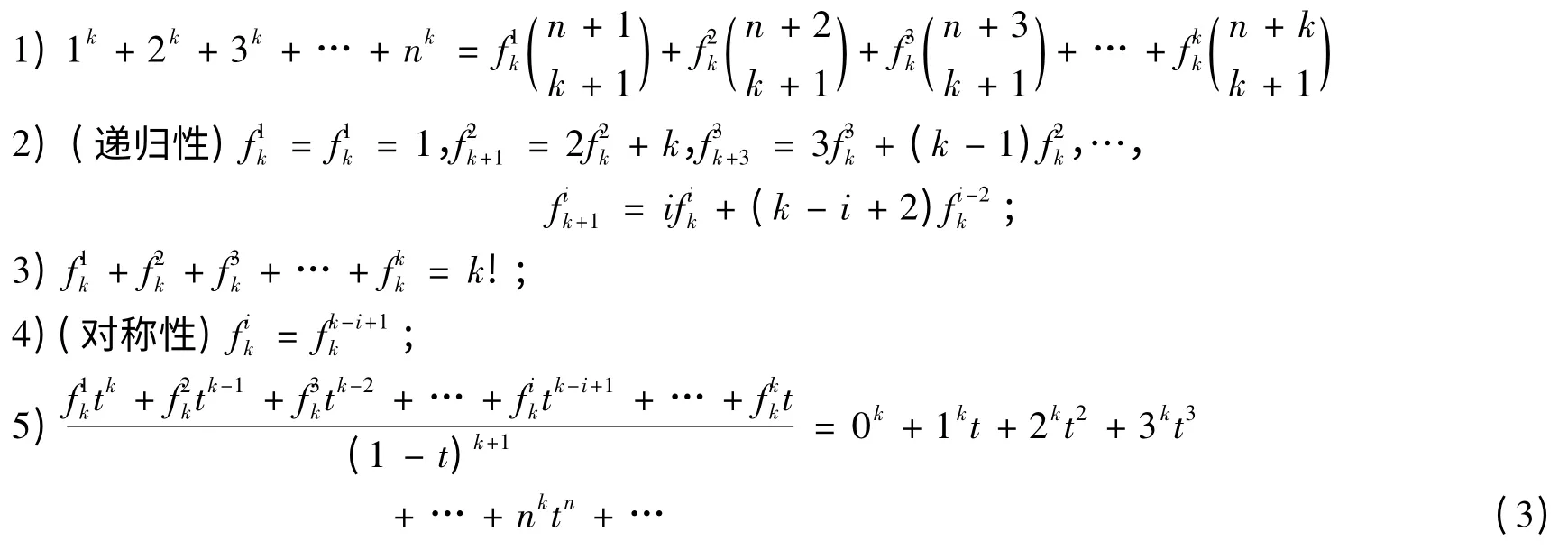
证明:当k=1,2,3时,上述5个结论都成立.假设对任一整数k,这5个结论都成立,(3)式两边对t求导,得
左边分母=(1-t)2k+2,约去分子分母的公因式(1-t)k,得
展开上述多项式并合并同类项,得
tk的系数为
tk-1的系数为
tk-2的系数为
tk-3的系数为
………
tk-i+1的系数为:
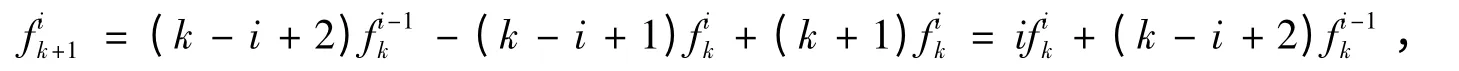
………
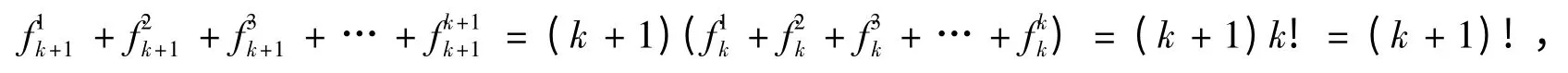
因此,对(3)式经过微分后,得:

用t乘以(4)式的两边,得:
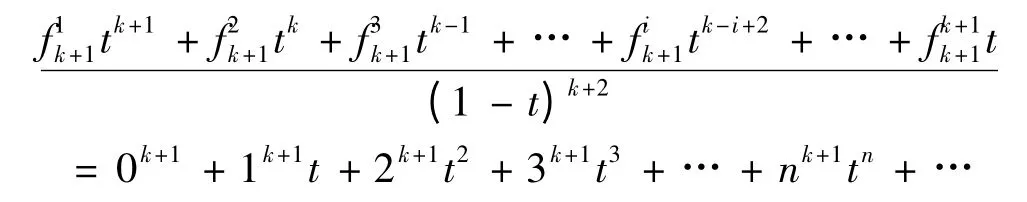
由引理1.1,数列 {0k+1,0k+1+1k+1,0k+1+1k+1+2k+1,…,0k+1+1k+1+2k+1+…+nk+1,… }的生成函数为:

即
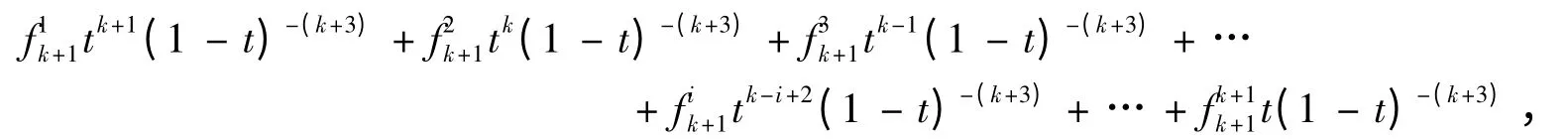
展开这个多项式,并考虑tn的系数,有

由数学归纳法,定理2.1中结论1)、2)、3)及5)都成立.
假设表1中前k行元素是对称的,且

下面证明

由递归关系


定理2.2 表1中各行元素是对称的,且在左半行,元素递增:在右半行,元素递减
证明:假设当k=2h时,在第2h行的左半行的元素是递增的,即
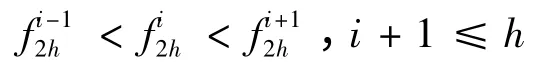
由递归关系


因此,在第2h+1行的左半行内元素也是递增的.
假设当k=2h+1时,在第2h+1行的左半行的元素是递增的,即

由递归关系

由此可得,在第2h+2行的左半行内元素是递增的.
由数学归纳法,在表1中任一左半行内的元素是递增的.根据对称性知,任一右半行内的元素是递减的.
[1]吴顺唐.离散数学[M].上海:华东师范大学出版社,2011.
[2]李宇寰,组合数学[M].北京:北京师范学院出版社,1988.
[3]曹汝成.组合数学[M].广州:华南理工大学出版社,2000.
[4]孙淑玲,许胤龙.组合数学引论[M].北京:中国科学技术大学出版社,1999.
[5]李大超,尚世奇.组合和的几个计算公式[J].高校应用数学学报(英文版),2002,17(1):119-124.
[6]李国庆,程林凤.组合问题中生成函数的应用[J].彭城职业大学学报,2001,(2):75-76.
[7]娄源冰,生成函数的应用[J].西藏大学学报,2000,15(2):78-79.
[8]陈军科.生成函数及其应用[J].科学技术与工程,2011,11(19):4547-4549.
[9]王新渊.生成函数在数列研究中的应用[J].青海大学学报(自然科学版).2000(3):44-45.
[10]冯素芬,刘永现.生成函数计数理论的应用及其最新进展[J].北京工业职业技术学院学报,2008(2):62-64.
