基于混合粒子群算法的单杆柔性臂LQR位置控制优化设计

基于混合粒子群算法的单杆柔性臂LQR位置控制优化设计*

路恩，杨雪锋，李威，刘玉飞，鞠锦勇

(中国矿业大学 机电工程学院，江苏 徐州221116)

摘要：针对单杆柔性机械臂LQR(linear quadratic regulator)控制中加权矩阵参数的选择问题，提出了一种基于混合粒子群算法寻优加权矩阵参数的方法。首先，基于假设模态法和拉格朗日方程建立了单杆柔性臂的动力学模型，并推导出系统的控制模型。引入了遗传算法中交叉操作以加强粒子群算法中粒子间区域的搜索能力，改进了基本粒子群算法易陷入局部最优的问题。最后，仿真结果表明基于混合粒子群算法迭代寻优得到的加权矩阵参数与经验值相比具有更优的控制效果。而且，与传统采用的遗传算法优化加权矩阵参数方法相比，具有较快的搜索和收敛速度，且具有需要调节的参数少、概念简单、实现容易的特点。

关键词：柔性臂；LQR；混合粒子群算法；Simulink仿真

文章编号：1001-2265(2015)09-0049-04

收稿日期：2014-11-16；修回日期：2014-12-16

基金项目：*国家自然科学基金资助项目(51305444)；教育部博士点基金(20120095120013)；江苏省科技计划项目(BY2014028-06)；江苏高校优势学科建设工程资助项目

作者简介：路恩(1990—)，男，江苏沭阳人，中国矿业大学硕士研究生，研究方向微机电系统设计及应用，(E-mail)jsluen@163.com。

中图分类号：TH113.1；TG506

The Optimal Design of LQR Tip Position Control for Single Flexible Manipulators

Based on Hybrid Particle Swarm Algorithm

LU En, YANG Xue-feng, LI Wei, LIU Yu-fei, JU Jin-yong

(School of Mechatronic Engineering, China University of Mining and Technology, Xuzhou Jiangsu 221116, China)

Abstract：A optimization method of the weighted matrix parameters based on hybrid particle swarm algorithm is presented for the LQR control of single flexible manipulators. First, the dynamic model of the single flexible manipulator is established by the assumed mode method and the Lagrange equations. Then, the model of control system is derived by the dynamic model which is written as a matrix equation. The crossing operator of genetic algorithm is introduced into the particle swarm algorithm to strengthen the search ability of particles area, and improve the basic particle swarm optimization algorithm which is easy to fall into local optima. Finally, the numerical simulation results show that the control effects of the iterative optimization parameter of the weighted matrix based on the hybrid particle swarm algorithm is better than the method of experience value. In addition, when it was compared with the genetic algorithm, a traditional weighted matrix parameters optimization methods, the hybrid particle swarm algorithm has small number of tuning parameters, simple concepts and easy realization.

Key words： flexible manipulator;LQR;hybrid particle swarm algorithm; Simulink simulation

0引言

在现代控制理论中， LQR控制算法是一种广泛使用的方法，它采用状态控制法来分析系统，通过一个可以控制状态反馈增益值的LQR控制器，实现系统的稳定性控制[1]。由于LQR控制方法可以利用廉价成本使被控系统达到较好的性能指标，因而LQR控制方法在柔性臂末端位置控制中也得到了广泛的应用。例如，文献[2]基于柔性连接的机械臂的状态空间模型进行了LQR控制仿真；文献[3]基于末端挠度反馈，对柔性臂进行了LQR控制的仿真与实验分析。

LQR控制中的状态反馈增益K由加权矩阵Q与R唯一决定，故Q、R参数的选择尤为重要。然而，加权矩阵Q、R的选取没有统一的方法，通常是根据经验调节得到的，这样使得参数的选取具有较大的主观性，尤其在参数较多时很难找到较优的控制参数，因此需要一种简单、有效的优化算法进行参数寻优。粒子群算法是近年来发展起来的智能优化算法，其具有概念简单、容易实现、需要调节的参数偏少、求解速度快等特点，在许多领域得到了很好的应用。故本文提出了基于混合粒子群算法对LQR控制中加权矩阵Q、R进行参数寻优的方法，将遗传算法中的交叉操作引入到基本粒子群算法中，不但能提高搜索速度、收敛精度，且能够改进基本的粒子群算法易陷入局部最优的问题。

本文针对带有末端质量的单杆柔性臂位置控制，提出基于混合粒子群算法对LQR控制中Q、R参数选取进行优化。采用假设模态法和Lagrange方程推导出柔性臂的动力学模型，并由此推导出系统的状态方程；根据状态方程设计了LQR控制器，建立了Simulink仿真模型；基于混合粒子群算法，对LQR控制中Q、R参数进行了迭代寻优；结合仿真模型，对基于经验及粒子群算法求出的控制参数进行仿真对比，验证混合粒子群算法优化Q、R参数的有效性。

1仿真模型建立

1.1单杆柔性臂的动力学模型

单杆柔性机械臂的结构简图如图1所示。设OXY为固定坐标系；oxy为固连在柔性臂上的局部坐标系；u(t)电机驱动力矩；Jh为电机转轴及夹具的转动惯量；mL为柔性臂的末端质量；w(x，t)为柔性臂在局部坐标系下，t时刻P点的横向弹性变形；θ(t)为电机转角；E为柔性臂的弹性模量；ρ为柔性臂的密度；A为柔性臂的截面积；L为柔性臂长度。

图1　单杆柔性机械臂结构示意图

将柔性臂简化为Euler-Bemoulli梁，并忽略次要因素，利用Lagrange方程可建立如下的动力学方程。

(1)

其中，常系数J，Wi(L)，σi，Mi，Ki分别为

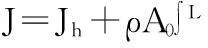
Wi(L)=cosh(βiL)-cos(βiL)-

Wi(x)=cosh(βix)-cos(βix)-

1.2控制系统模型

(2)

其中，常系数M, K, F分别为

M=

然而，实际情况中的柔性机械臂是有阻尼的，本文主要考虑关节阻尼和机械臂的结构阻尼。关节处的阻尼考虑为粘性阻尼，结构阻尼采用结构动力学中的比例阻尼，可得到如下阻尼矩阵[5]。

(3)

式(3)中CH为关节处粘性阻尼，α为质量阻尼系数,则，加入阻尼矩阵的动力学方程式如下:

(4)

由此可得出，单杆柔性臂线性定常系统的状态空间模型如下所示：

y(t)=Cx(t)

(5)

(6)

实际控制中主要考虑机械臂的末端位置，因此选取柔性机械臂的端部转角θL作为控制目标，即

(7)

2LQR控制器设计

单杆柔性机械臂末端位置的控制是典型的最优跟踪问题，然而线性二次型最优跟踪问题直接求解较为困难，因此，为便于容易实现，将此问题转化为无限时间的二次型定常调节器问题，所得到的定常调节器具有常增益形式[4]。

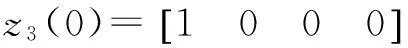
(8)

(9)

最优的控制力矩为

u=-Kx(t)

(10)

其中，K为最优控制反馈增益矩阵，可通过Matlab的线性二次型最优控制器设计函数获得[6]：

(11)

取前一阶模态进行仿真，因此可选取Q为4维半正定对角矩阵，R为1维正定矩阵。LQR最优控制中Q和R的选择是相互制约、相互影响的，故可选取R的值为1，Q可表示如下：

(12)

被控系统的Simulink模型如图2所示。

图2　被控系统的Simulink模型

3基于混合粒子群算法Q、R参数寻优

粒子群算法是模拟鸟群寻找栖息地而寻找最优解的方法，群粒子在飞行过程中不断向最优解靠拢，最后找到最优解。粒子群算法同遗传算法类似，是一种基于迭代的群体随机优化技术，但粒子群算法采用简单的速度-位置模型，避免了复杂的遗传操作，同时特有的记忆使算法可动态跟踪当前的搜索情况来调整其搜索策略[7]。此外，粒子群算法具有概念简单，容易实现，需要调节的参数偏少的特点。

设每个粒子维数为D，第i个微粒表示为Xi=(xi1,xi2,…,xiD)，经历过的最好位置(有最好的适应值)记为Pi=(pi1,pi2,…,piD)。在群体所有微粒经历过的最好位置的索引号用符号g表示，即Pg。微粒i的速度用Vi=(vi1,vi2,…,viD)表示。对每一代，它的第d维(1≤d≤D)根据如下方程进行变化：

速度更新：

位置更新：

其中，w为惯量因子，取值一般在(0，1)之间，Clerc[8]建议取值为0.729；c1、c2为加速度因子c1、c2通常选取为2，Clerc[7]建议(c1+c2)/2的取值为1.494；rand()为0~1之间的随机数。

交叉操作原本是遗传算法中三种遗传操作中的一种，是决定算法收敛性能的关键[9]，本文将其引入到基本的粒子群算法中。

在速度更新之后添加以下交叉操作：

在位置更新之后添加以下交叉操作：

此混合粒子群算法在基本的粒子群算法中的速度和位置的更新操作后添加上述的交叉操作，并且用产生的后代粒子取代双亲粒子。交叉操作使后代粒子继承了双亲粒子的优点，在理论上加强了对粒子间区域的搜索能力[10]。例如，两个双亲粒子均处于不同的局部最优区域，则两者交叉产生的后代粒子往往能够摆脱局部最优，从而改进搜索结果[9]。

图3　混合粒子群算法优化设计LQR控制器示意图

4数值仿真及结果分析

假定柔性臂在电机的驱动下转动位移为1rad，进行末端位置控制，单杆柔性机械臂的结构参数如表1所示。

根据仿真参数，控制参数可取如下经验值：q1=35，q2=15，q3=2，q4=15

控制参数迭代寻优的取值范围如表2所示，经过混合粒子群算法迭代寻优可知：

q1=38.4679，q2=16.2774，q3=3.3714，q4=16.4305

寻优曲线如图4、图5所示，位置控制仿真曲线如图6、图7所示。

表1　单杆柔性机械臂的结构参数

表2　控制参数取值范围

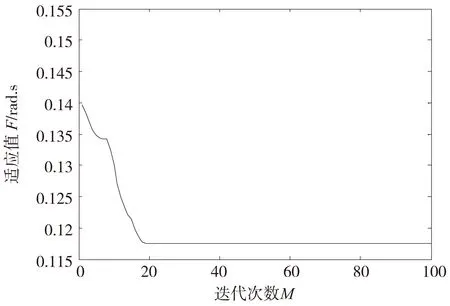
图4　最优个体适应值

图5　加权矩阵Q参数优化曲线

图6　单杆柔性臂末端位置仿真曲线

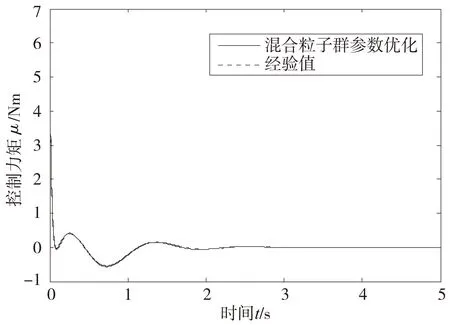
图7　单杆柔性臂控制力矩仿真曲线

从图4和图5中可以看出，基于混合粒子群算法不仅实现简单，而且具有较快的搜索速度，能快速准确的找到较优的控制参数。从图6可以看出，基于混合粒子群算法寻优的加权矩阵参数与经验值比较，具有更快的响应速度，更小的超调，达到了较优的控制效果。图7为单杆柔性臂控制力矩仿真曲线，两者曲线比较接近。

5结论

本文针对单杆柔性臂末端位置LQR控制中加权矩阵Q、R参数选取的问题，提出了基于混合粒子群算法，对Q、R参数进行迭代寻优。相较遗传算法，采用混合粒子群算法对加权矩阵参数进行寻优具有概念简单、容易实现、需要调节的参数少、求解速度快等优点。最后，结合柔性臂仿真模型，对基于经验及粒子群算法求出的控制参数仿真表明混合粒子群算法搜索的速度较快，并与经验值比较，对柔性臂末端起到了更优的控制效果，验证了混合粒子群算法的有效性。

[参考文献]

[1] Liu Z X, Yuan C, Zhang Y M, et al.A learning-based fuzzy LQR control scheme for height control of an unmanned quadrotor helicopter[C].//2014 International Conference on Unmanned Aircraft Systems (ICUAS). Piscataway: IEEE, 2014. 936-941.

[2]袁浩，乔宇亮，李宝林,等. LQR控制策略在柔性关节系统中的实现[J]. 实验技术与管理,2006，23(8)：33-35.

[3] Mariam Baroudi, Mohamad Saad, Walid Ghie. State-Feedback and Linear Quadratic Regulator Applied to a Single-Link Flexible Manipulator[C].//2009 IEEE International Conference on Robotics and Biomimetics (ROBIO 2009), Piscataway: IEEE, 2009.1381-1386.

[4]汪性武. 柔性机械臂的振动控制[D].南京:南京航空航天大学, 2004.

[5]杨辉. 刚-柔耦合动力学系统的建模理论与实验研究[D].上海:上海交通大学, 2002.

[6] 刘晓培. 基于遗传算法的汽车主动悬架LQR控制器的优化设计[J]. 组合机床与自动化加工技术,2013 (6): 78-80.

[7]陈自郁. 粒子群优化的邻居拓扑结构和算法改进研究[D].重庆:重庆大学,2009.

[8] Clerc M,Kennedy J. The Particle Swarm-Explosion, Stability, andConvergence in a Multidimensional Complex Space[J]. IEEE Transactions on Evolutionary Computation, 2002, 6(1): 58-73.

[9] 蔡良伟，李霞. 遗传算法交叉操作的改进[J]. 系统工程与电子技术， 2006，28(6)：925-928.

[10] 潘峰，李位星，高琪,等. 粒子群优化算法与多目标优化书[M]. 北京：北京理工大学出版社，2013.

[11] 滕悠优. 柔性机械臂的主动控制与实验研究[D]. 上海:上海交通大学, 2007.

(编辑李秀敏)