一种炮兵射击炸点精确仿真方法

聂　浩，吴正龙

(陆军军官学院，合肥　230031)

一种炮兵射击炸点精确仿真方法

聂浩，吴正龙

(陆军军官学院，合肥230031)

摘要：炸点仿真对于炮兵射击效率评定、作战模拟等具有重要意义；提出了一种适用于炮兵营以下射击的炸点精确仿真方法，单独考虑分火射击时同一火炮不同表尺上的炮单独误差表征；仿真实验表明:不论是集火射向一距离射击，还是适宽射向,三距离射击，距离和方向偏差以及方差都能很好收敛，并且能比较好的接近理想值。因此，方法可以得到严格符合射击误差表征的炸点分布。

关键词：射击误差；正态分布；方差

炸点仿真对于炮兵射击效率评定、作战模拟等具有重要意义。特别是新型弹药的毁伤效能分析研究中，由于实弹试验代价高昂，一般采用MonteCarlo方法在计算机上模拟射击，用仿真的炸点来模拟弹药实射的落点，进而分析弹药对目标的毁伤效能[1-2]。此时，计算机模拟炸点的真实性，极大程度上决定了毁伤效能分析结果的可信度。一般而言，对于特定武器系统，其炸点分布律是确定的。炸点仿真就是要运用计算机仿真方法，产生严格符合武器系统射击误差表征的炸点。

1基本概念

炮兵射击中，任意一发炸点对瞄准位置的偏差量称为发射误差[3,4]。构成发射误差的任何一个误差因素或数个误差因素的综合，统称为射击误差。

给出假定：射击单位不大于炮兵营，营内各连阵地配置较接近，因此可近似认为对同一目标射击时各炮之间射距离和射击方向的差别可以忽略不计，当任何一项射击误差按营(连)的平均射击方向分解为距离误差和方向误差时都可认为之间相互独立[5]。对于18门制炮兵营，通常情况下符合该假定。如配置很分散，则需按炮兵群射击的情况处理，不在本文讨论范围之内。图1给出各组射击误差及其相互关系。

在求得营共同误差、连单独误差、炮单独误差的距离和方向中间误差(Exyg,Ezyg)、(Exl,Ezl)、(Exp,Ezp)后，连共同误差、诸元误差、发射误差的距离和方向中间误差(Exlg,Ezlg)、(Edp,Efp)、(Edf,Eff)可由式(1)求得，其中射弹散布距离和方向公算偏差Bd和Bf可从射表查得

(1)

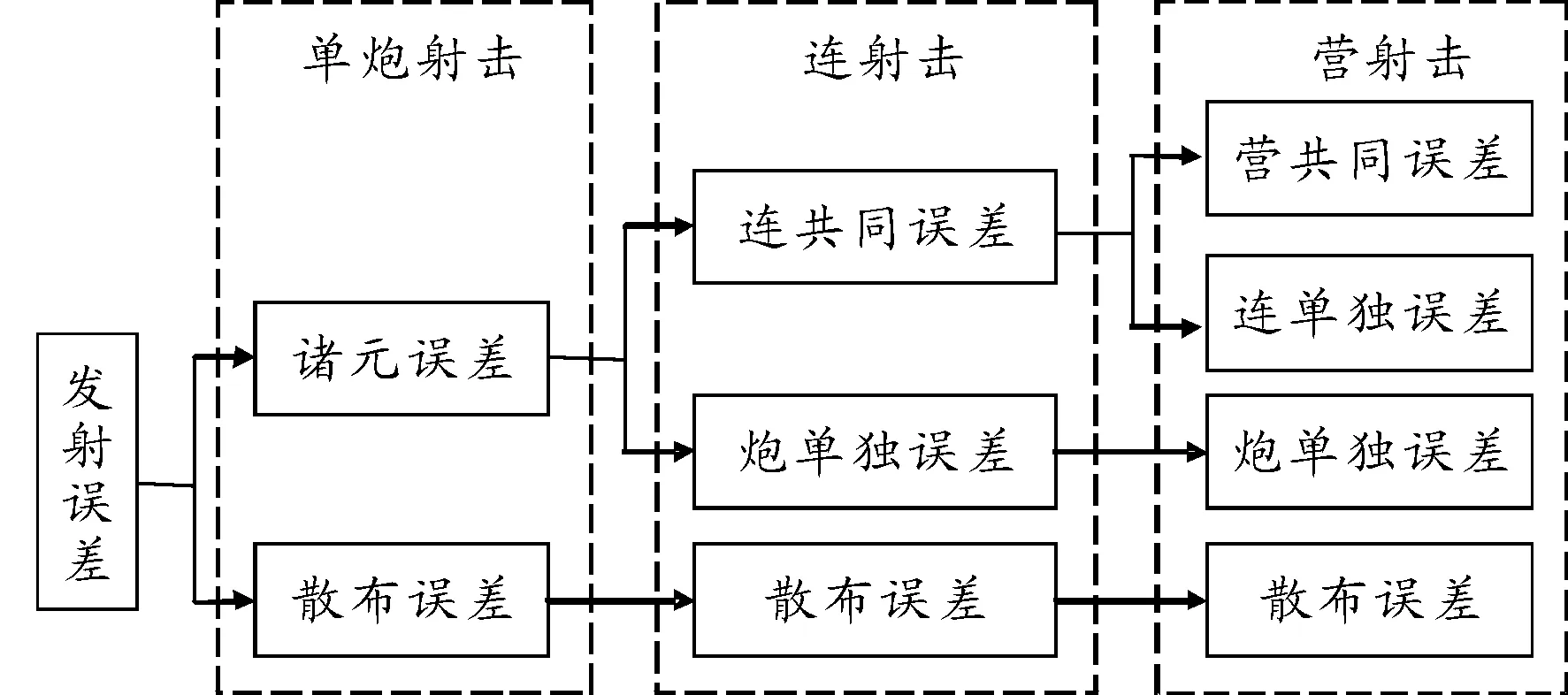
图1　射击误差分组及相互关系

2炸点分布

炸点分布指在发射多发射弹时由于各组射击误差以及火力分配方法的不同而形成不同的炸点分布景况，通常可以用分布中心位置以及炸点对分布中心的距离和方向偏差量X、Z的联合概率密度函数和它们的方差或均方差来表示[6]。分布中心位置的期望值为瞄准中心。

当n门制炮兵连以集火射向一距离射击时，其任一发炸点对炸点分布中心的距离和方向偏差量Xb和Zb的方差D(Xb)、D(Zb)为

(2)

当m连n门制炮兵营以I的射向间隔，h的距离差行t个距离射击时，如各分划上发射弹数相同时，则D(Xb)、D(Zb)为

(3)

3炸点仿真算法

本算法假定射击条件为炮兵营射击。炮兵营有m个连，每连有n门火炮。纵向与射击方向一致。瞄准点位置取目标中心。行适宽射向、t个表尺分划射击，距离差hx，射向间隔IO，每表尺上发射N1发炮弹，全营共发射N=mntN1发炮弹。营共同距离和方向中间误差为Exyg和Ezyg，连单独距离和方向中间误差为Exl和Ezl，炮单独距离和方向中间误差为Exp和Ezp，散布距离和方向中间误差为Bd和Bf。对于连、单炮以及集火一距离等各种其他射击，均可通过m、n、t、hx、IO以及各误差表征的不同取值得到[7-9]。

对于营内各连，虽然连单独误差表征值一样，但连单独误差数值并不相同，同样，连内各炮的炮单独误差数值也不相同。不仅如此，由于每门火炮要以3个表尺射击，相当于有3个瞄准位置，因此，对于某门火炮来说，其在不同表尺上的炮单独误差表征值都不相同。通过分析炮单独误差的误差源可知，导致误差表征值不同主要是由技术准备引起的[10](因要改变射角射向)。一般而言，对于152JLP，技术准备引起的距离和方向中间误差占炮距离和方向中间误差的比重可分别取3%和6%。

将正态随机数生成子过程记为sub_randg，其算法：首先产生k个0~1之间服从均匀分布的随机数，记为A1,A2,…,Ak，A*为k个随机数均值，则可由式(4)计算得到一个数学期望是0中间误差为1的正态随机数w，且数学期望为xc中间误差为Ex的正态随机变量x=xc+Exw

(4)

炸点仿真算法程度为

fork=1tomdo

w1=sub_randg;w2=sub_randg;

xl=xy+Edl*w1;zl=zy+Efl*w2;

forj:=1tondo

w1=sub_randg;w2=sub_randg;

xpo=xl+sqrt(Edp*Edp*0.97)*w1;

zpo=zl+sqrt(Efp*Efp*0.94)*w2;

fori=1totdo

xc=xpo+(i-(t+1)/2)*hx;

zc=zpo+(j-(n+1)/2)*io;

w1=sub_randg;w2=sub_randg;

xc=xc+sqrt(Edp*Edp*0.03)*w1;

zc=zc+sqrt(Efp*Efp*0.06)*w2;

forl=1toN1do

w1=sub_randg;w2=sub_randg;

x=xc+Bd*w1;z=zc+Bf*w2;

算法共得到每炮每个表尺上炸点位置N1个抽样值，共得到mntN1个抽样值，此即可作为符合射击误差表征的模拟炸点。

4实验与结论

18门制152JLP炮兵营，在决定诸元误差分析中已得出各射击误差表征为

Exyg=40m, Ezyg=16m, Exl=30m, Ezl=12m, Exp=36m, Ezp=18m

从射表中查出Bd=20m, Bf=4m。对以下射击条件下炸点进行仿真。

(1)用一个连以集火射向一距离射击。

(2)炮兵营以50m的射向间隔和2Bd的距离差行三距离射击，所有分划上发射弹数相同。

对射击条件(1)和(2)分别运用炸点仿真算法进行20 000 次仿真，图2和图3分别给出其中某一次炸点分布情况(每炮每表尺发射弹数1 000发)。

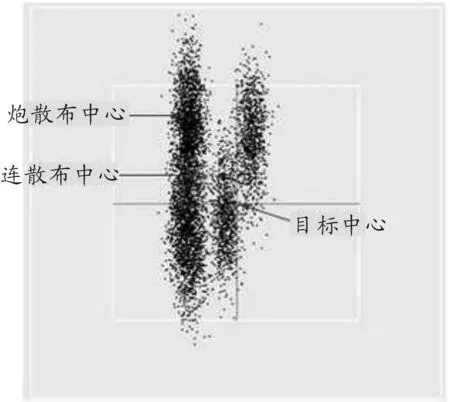
图2　连集火射击炸点分布

图3　营适宽射向三距离射击炸点分布

绘出平均的炸点分布中心对目标中心(中心瞄准位置)的距离和方向偏差量变化图如图4(a)、图4(b)所示，以及任意一发炸点对炸点分布中心的距离和方向偏差量的平均方差(D(Xb)、D(Zb))变化图如图4(c)、图4(d)所示。

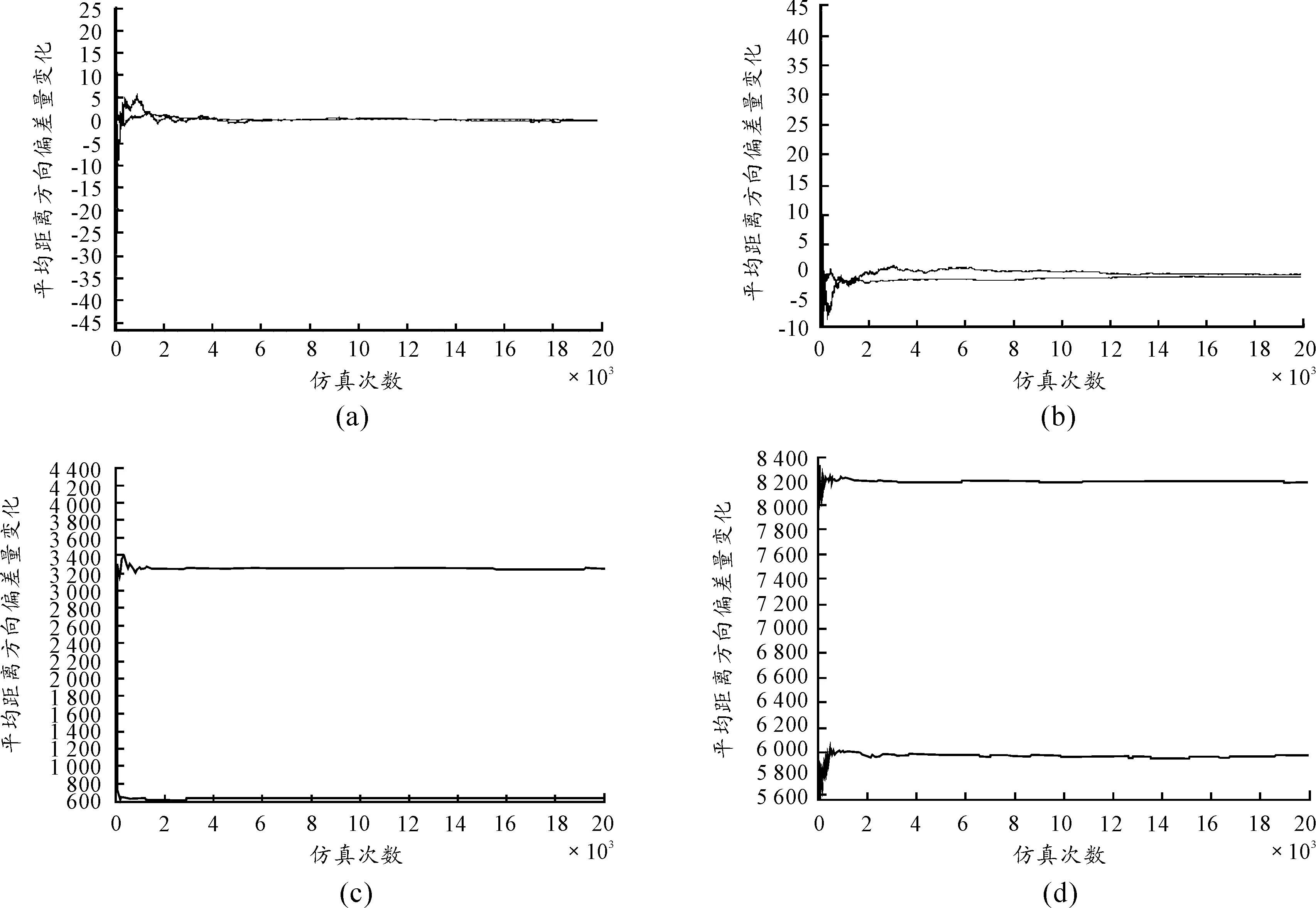
图4　距离、方向偏差量及其方差变化

根据式(2)和式(3)，可分别求得在射击条件(1)和(2)情况下D(Xb)和D(Zb)的理想值，其与仿真平均值的对比如表1所示。

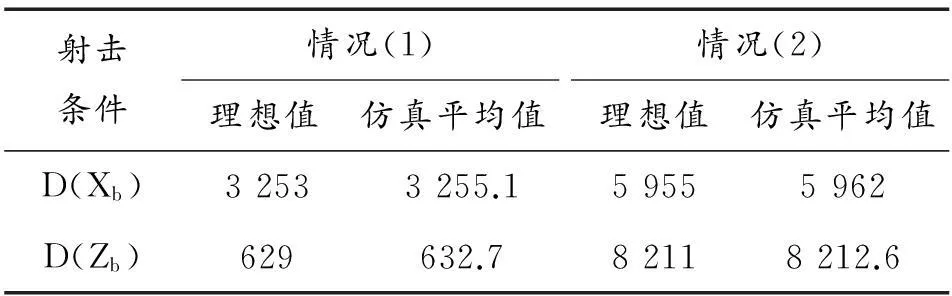
表1　炸点分布方差理想值与仿真平均值对比

可以看出，不论是连集火射向一距离射击，还是营适宽射向三距离射击，距离和方向偏差以及方差都能很好的收敛，并且能比较好的接近理想值。因此，该炸点模拟方法可以得到较严格符合射击误差表征的炸点分布。

参考文献：

[1]吴正龙,王大鹏.基于仿真弹群的目标毁伤预测模型[J].火力与指挥控制,2012(9):67-70.

[2]吴正龙,赵忠实.基于自适应模糊神经网络系统的射击毁伤评估模型研究[J].兵工学报,2012(11):1352-1357.

[3]吴大梁.射击效果的评定及最优化方法[M].南京炮兵学院出版社,1986.

[4]刘怡昕.炮兵射击学[M].北京：海军出版社,2007.

[5]江华,许梅生.炮兵射击基本理论分析[M].北京：兵器工业出版社,2004.

[6]程云门.评定射击效率原理[M].北京：解放军出版社，1986.

[7]聂鹏,曹兵.破片式战斗部对空中飞机的毁伤建模与仿真[J].指挥控制与仿真,2012(6):80-83.

[8]曾前腾,吴慧中.基于C~4ISR的空炸射击高炮拦阻射击效力仿真研究[J].兵工学报,2007(10):1164-1168.

[9]单显明,肖俊岭.炮兵雷达组网校射评估系统的设计与实现[J].指挥控制与仿真,2010(4):94-96.

[10]王亮宽,舒立鹏,程广伟.配用AHEAD弹高炮武器系统射击效率模型[J].火炮发射与控制学报,2010(2):5-8.

[11]王兆胜. 平均子弹群中心法在子母弹射击效率计算上的应用[J].兵工自动化，2013(6):1-3.

(责任编辑周江川)

收稿日期：2015-02-12

作者简介：聂浩(1989—)，男，研究生，主要从事目标毁伤与终点效应研究。

doi:10.11809/scbgxb2015.07.012

中图分类号：TJ015

文献标识码：A

文章编号：1006-0707(2015)07-0042-04

本文引用格式：聂浩，吴正龙.一种炮兵射击炸点精确仿真方法[J].四川兵工学报，2015(7):42-44.

Citationformat:NIEHao,WUZheng-long.MethodofArtilleryBombedPositionSimulation[J].JournalofSichuanOrdnance,2015(7):42-44.

MethodofArtilleryBombedPositionSimulation

NIEHao,WUZheng-long

(ArmyofficerAcademy,Hefei230031,China)

Abstract:Simulation of impact position is significant to the artillery efficiency evaluation and the battle simulation. A method of exact Simulation of impact position was proposed, which is applied to artillery units at the battalion level and below in the fields, in consideration of gun individual error integration in different rear sight in the same gun during multiple armament datum firing separately. Simulated experiments show that error and variance of distance sand direction would be of convergence well whenever concentration firing or optimum width fire or three-distance fire, and they could be greatly close to the ideal data. So, bombed position distribution which fits to firing errors rigidly could be calculated in this method.

Key words:firing errors; normal distribution; variance

【装备理论与装备技术】