黎曼可积的测度论观点
2015-12-30徐艳艳陈广贵
徐艳艳 陈广贵 田 萍
(1.数字空间安全保障四川省高校重点实验室,四川 成都610039;2.西华大学理学院,四川 成都610039)
16世纪,迫于力学和天文学等基础学科的发展需求而创立的微积分学不仅带动了各个基础学科的发展,也催生出了全新的数学学科——分析学,然而在18世纪末19世纪初,数学家们逐渐发现了分析学中的种种问题,看似强大的黎曼积分[1,3,7,9]已不足以满足数学家们的追求乃至基础学科的发展需求,从黎曼积分的定义可以清楚的发现,黎曼积分关心的是一个在有限区间上有界的函数对于一个与它紧密相关的式子的极限是否存在的问题,而寻求极限存在与否的条件成了重中之重,这时一个显而易见的问题浮现出来:函数要满足怎样的条件该极限才会存在?换句话说函数需要满足何种条件才能够黎曼可积?黎曼积分理论中虽给出了一个判别定理但却几乎无实用性可言.为此我们将借助建立在测度论基础上的Lebesgue积分理论对一个函数在区间上的黎曼可积性做出判断,力图寻求一个更为简单实用的判别定理,并利用他们解决了一些在数学分析中不易解决的问题,这便是本文的核心.下面我们就用测度论的观点来叙述黎曼可积条件.
设在[a,b]上定义函数f(x)(不一定是有限的),设δffgt;0,函数f(x)在(x0-δ,x0+δ)上的下确界与上确界分别记以mδ(x0)与Mδ(x0),即
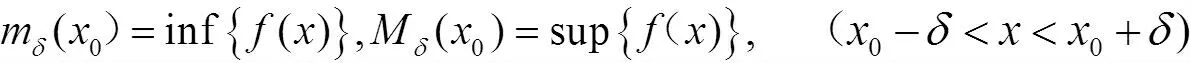
(在(x0-δ,x0+δ)中,自然只考虑也含在[a,b]中的点)
显然的是mδ(x0)≤f(x0)≤Mδ(x0).
当δ变小时,mδ(x0)决不减少而Mδ(x0)决不增加.因此有如下极限:
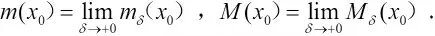
并且显然有mδ(x0)≤m(x0)≤f(x0)≤M(x0)≤Mδ(x0).
定义1 函数m(x)与M(x)分别称为f(x)的贝尔下函数与贝尔上函数.
引理1[2]设f(x)在x0是有限的.函数f(x)在x0为连续的必要且充分的条件是
m(x0)=M(x0).

推论1 贝尔函数m(x)及M(x)都是可测的.
事实上,分点{x(ki)}的全体是一可数集,其测度为0.因此由引理2,φi(x)几乎处处收敛于m(x).因为φi(x)是阶梯函数,所以是可测的,因此m(x)也是可测的.同样M(x)也是可测的.
推论2 假如引理2中的函数是有界的,那么
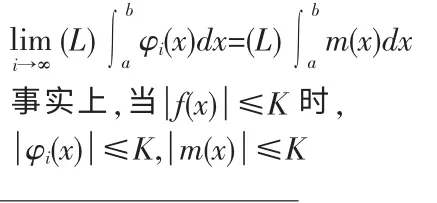
因此φi(x)与m(x)都是(L)可积函数.
在此基础上我们对推论2作进一步解释.注意到
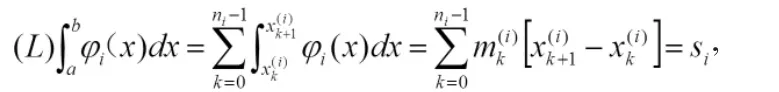
其中si是由第i个分法所得的达布小和.于是,推论2表示
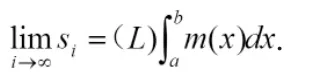
另一方面,在分析课程中,已证明有界函数f(x)为黎曼可积的必要且充分条件是Si-si→0.
所以有界函数f(x)为黎曼可积的必要且充分条件是

由(1)式当M(x)-m(x)等价于0时是成立的.反之,由于M(x)-m(x)≥0,从条件(1)得M(x)↔m(x). (2)
于是,有界函数f(x)为黎曼可积的必要且充分条件是(2)式成立.
由此便得出本文的中心论点:
定理1 (Lebesgue判别法)[a,b]上的有界函数f(x)为(R)可积的必要且充分的条件是f(x)在[a,b]上是几乎处处连续的.
下面再给出Lebesgue判别法的另一种描述:
定理2 如果f(x)是区间[a,b]上的有界函数,则f(x)在[a,b]上黎曼可积的充分且必要条件是它在[a,b]中不连续点所构成的集合E的测度为0.
由定理1我们可以看出仅有那些较为连续的函数才可能黎曼可积,这里的较为连续应理解为不连续点的测度不得大于0的函数.因此从某种角度来说,黎曼积分是专门为“连续”函数而创造的.相比之下Lebesgue积分表现出了巨大的优势,不仅对于黎曼积分能够实现的“连续”函数进行积分,而且对于许许多多黎曼积分无可奈何的函数都能实现积分,较为出名的一个例子便是对于狄利克雷函数的积分(对于这个函数我们将在接下来的内容中作出详细介绍),这是一个极为不连续甚至可以说和连续定义毫不沾边的函数,但却可以十分轻易的对它实现Lebesgue积分.这是黎曼积分难以企及的.
Lebesgue积分较黎曼积分的范围要广很多,不难得出:凡有界可测函数依照Lebesgue的意义是可积的.特别是,许多与判定可积性有关的问题,到此就迎刃而解,不像黎曼积分中那样麻烦.
下面我们来看看测度论的观点在黎曼积分中的应用.
例1 狄利克雷函数
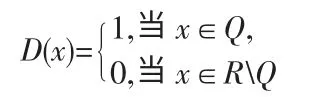
该函数在区间[0,1]上不可以黎曼可积,因为对任何分划P,在其中每个区间Δi中都能找到一个有理数ξ′i和一个无理数ξ″i.因此,
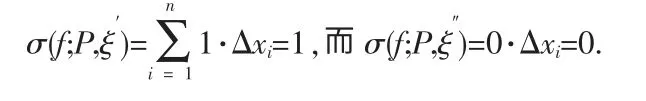
如此,当λ(P)→0时函数D(x)的积分和不可能有极限.然而从Lebesgue积分理论来讲,它是可积的,因为狄利克雷函数是明显可测的.且D(x)与f(x)=0,(x∈[0,1])是等价的,由此

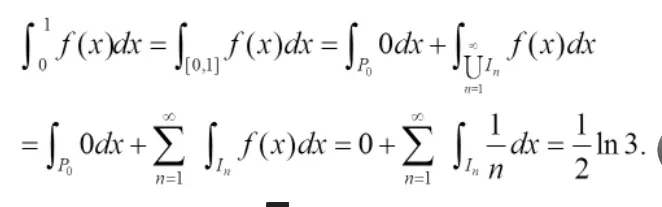
[1]陈纪修,於崇华,金路.数学分析(上、下)[M].北京:高等教育出版社.
[2]那汤松.实变函数论[M].5版.徐瑞云,译.北京:高等教育出版社.
[3]B.A.卓里奇.数学分析(第1卷)(第4版)[M].蒋铎,等,译.北京:高等教育出版社.
[4]程其襄.实变函数与泛函分析基础[M].北京:高等教育出版社,2003:52-167.
[5]江泽坚,吴智泉.实变函数[M].北京:高等教育出版社,1994:145-146.
[6]周民强.实变函数论[M].北京:北京大学出版社,2002:145-267.
[7]华东师范大学数学系.数学分析[M].北京:高等教育出版社,1991:319-331.
[8]张勇,杨光崇.数学分析(上册)[M].北京:高等教育出版社,2010:270-285.
[9]许天周.应用泛函分析[M].北京:高等教育出版社,2001.
