线性回归模型的一种新有偏估计
2015-12-29
线性回归模型的一种新有偏估计
隋丹阳1鄂英力2
1辽宁装备制造职业技术学院 (沈阳 110161) 2高明实验学校(沈阳110000)
摘 要在线性回归模型2下给出了有偏估计,其中K>0, c > 0为参数,∗表示线性回归模型的广义最小二乘估计,讨论了这种有偏估计的优良性质,得出了主要结论。
关键词有偏估计 广义最小二乘 岭估计
0引言
考虑线性回归模型:
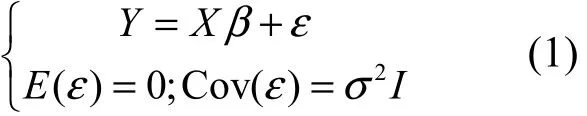
其中,Y是n×1观测向量,X是n× p列满秩设计阵,
β是p×1未知参数向量,ε为n×1随机误差向量。最小二乘估计是线性无偏估计类中方差最小的,但是当模型(1)存在复共线性时,最小二乘估计:
变得极不稳定[1],其均方误差为XTX的特征
值)趋近于无穷大,LS估计的性能变得很差,特别是在经济问题中,回归参数的经济意义往往得不到合理的解释。近几十年来,统计学家们针对最小二乘估计的改进做了很多研究,他们从消除多重共线性或减小估计的均方误差出发,提出了各种新的估计方法,诸如岭估计、压缩估计、主成分估计、特征估计等。在实际应用中岭估计无疑是最常用的一种有偏估计,因此人们对岭估计的研究倍加重视,为了进一步改进它的性质[2,3],人们提出了种种修正岭估计的方法,在一定条件下都可以优于岭估计。一般而言,对模型的限制越少越好,这样在实际应用中适用的范围才会更广,并且在实际情况中,线性模型的误差并不总是等方差且不相关的[4]。
1新估计的提出
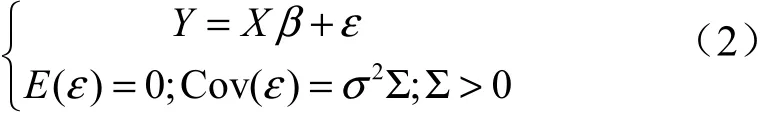
本文将模型推广到奇异线性模型中:且模型(2)的广义最小二乘估计[5]为。
为了便于讨论这种估计的性质,对模型(2)作一个适当的变化:,得到
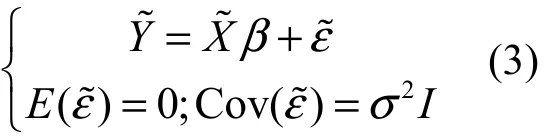
考虑模型(3)的典则形式:设2
1
p
λ λ λ
我们将对广义岭估计[6]做进一步改进,给出模型(2)的一个新估计:
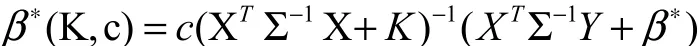
∗的一些性质
性变换。
证明:因为
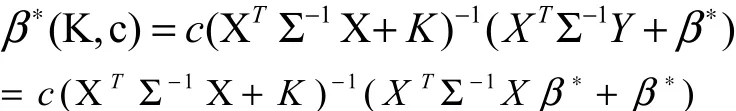
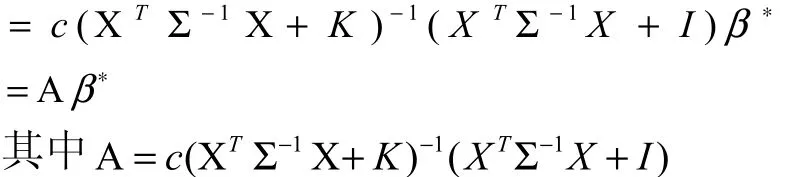
性质2. β(K,c)
∗是β∗的有偏估计。证明:
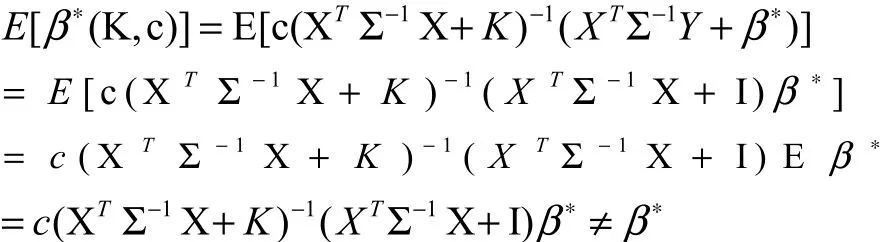
性质3. 对任意的k> c >0,β∗(K, c )是β∗的压缩,即
i。
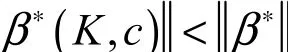
证明:对实对称阵,T1X∑−X进行Schur分解。
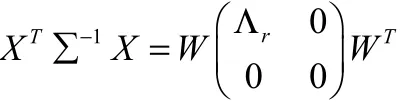
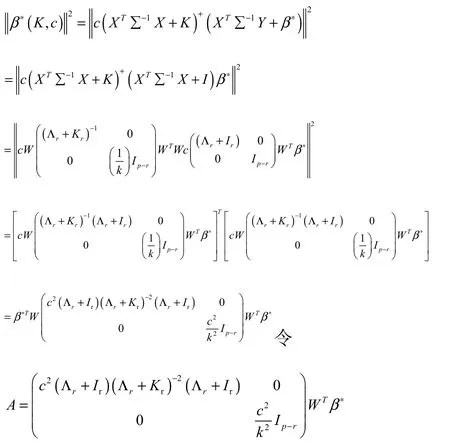
又因为0
因此,I− A>0,因为W为正交阵,所以有( )T0
可得
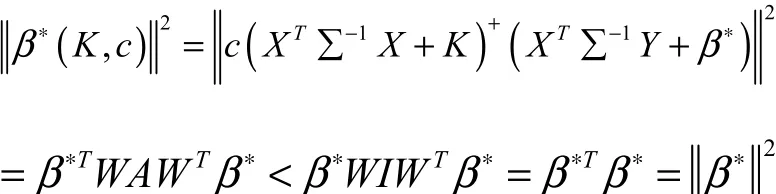
性质4.对任意的0
i
k> c >,α(K,c)
∗是α∗向原点的压缩。
证明:由模型(3)的典则形式可知
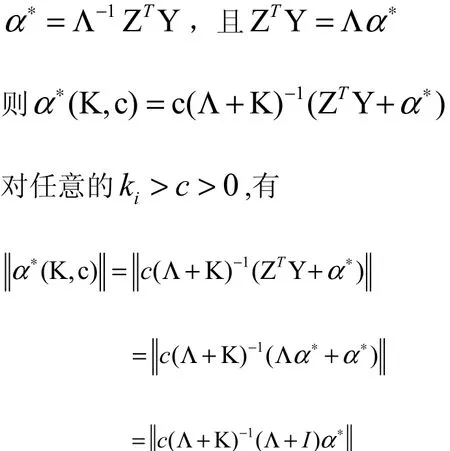
性质5.
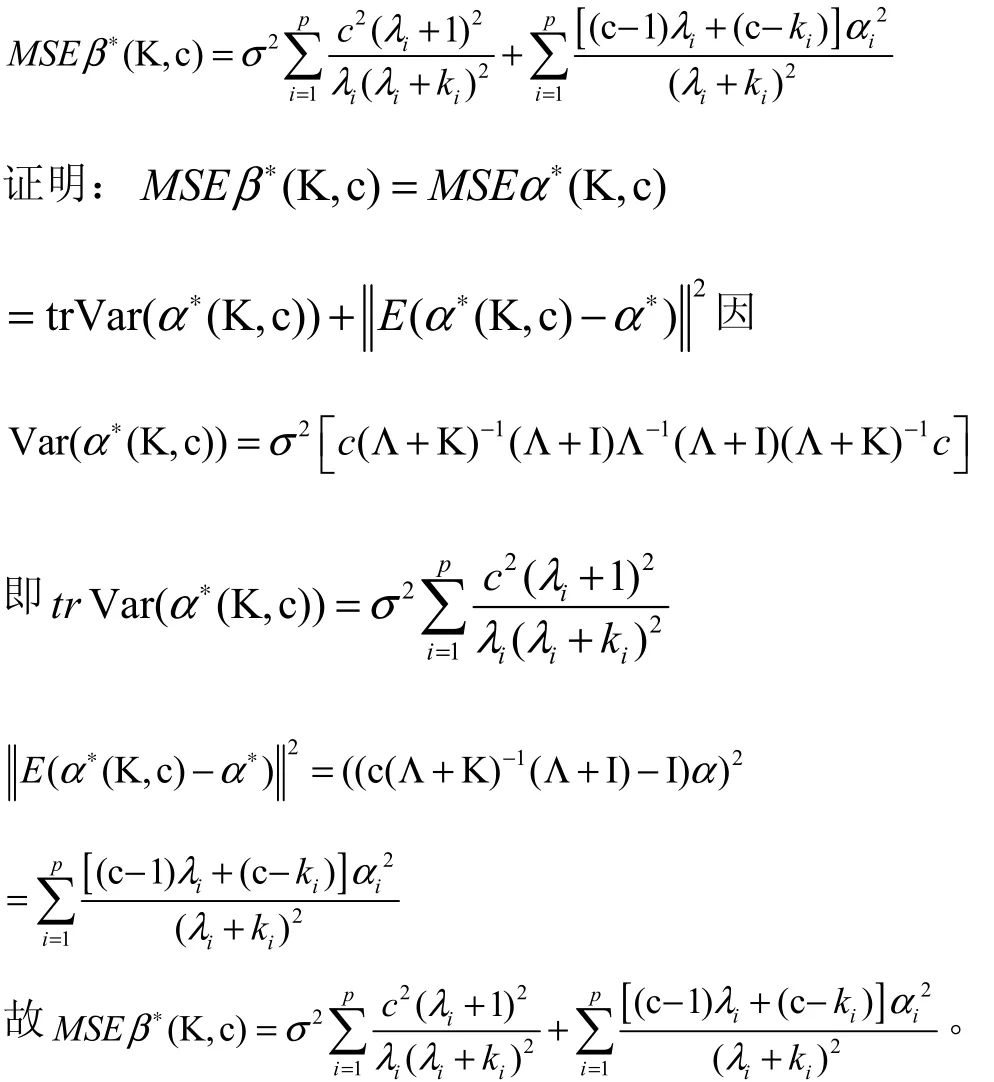
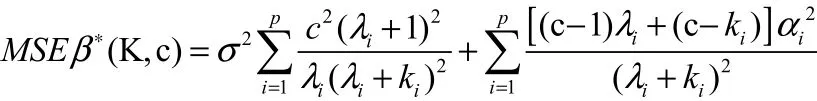
将上式分别对1,2, ,pk kk求偏导数,并令其为零,得

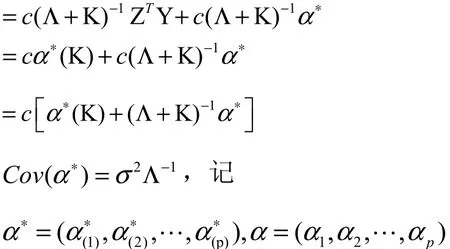

参考文献
[1]王松桂.线性模型的理论及其应用[M].合肥:安徽教育出版社,1987.
[2]张建军,吴晓平.线性回归模型系数岭估计的改进研究[J].海军工程大学学报,2005,17(1):54-57.
[3]张伟. 线性回归模型的一种有偏估计[J].武汉大学学报,2006,52(3):281-285.
[4]赵天玺,李兆勤.回归系数的一种有偏估计[J].重庆工商大学学报.2007,24(6):541-614.
[5]王松桂,史建红,尹素菊. 线性模型引论[M].北京:科技出版社,2005.
[6]郭效金.广义岭估计的新定义及其性质[J].河南教育学院学报,2003,12(1):35-36.
(责任编辑:林城)
