分治策略在归并排序中的算法设计
2015-12-29李六杏
李六杏
(安徽经济管理学院,安徽 合肥 230031)
分治策略即算法设计中的分治法.它的基本思想:对于那些规模较大的问题,我们难以直接解决,通常将其分解成若干个相互独立、易于解决的小问题,然后再通过递归算法,求出这些子问题,将这些子问题进行合并后的解,即可得到较大的原问题的答案.分治策略就是通过减小问题的规模,将大的问题化解成若干个小问题后逐步求解,这样能够大大降低了问题的复杂程度,提高了解决问题的效率.本文利用分治策略对归并排序进行改进算法设计,并与其它算法进行分析比较.
1 分治策略的适用条件
分而治之是一种解题的方法,其基本思路是:“如果一个大问题比较复杂,就可以将这个问题分解,然后各个击破.”分治从字面上包含了“分”和“治”两层含义,那么如何分,分后又如何“治”就成为我们解决问题的关键之处.通常并不是所有的问题都可以采用分治策略,只有那些能将问题分解成与原问题相似的、意思接近的子问题,并且再合并以后依然符合原问题的意思的这些问题,才能适用分治策略[1].一般的,能够使用分治算法解决的问题有以下几点特征:
(1)此问题在规模上可以缩小到一定的程度就能很容易地解决.一般的问题都能满足这个条件,这是因为一般问题的计算复杂性都是随着问题规模的增大而增大;
(2)此问题能够分解成若干个类似的规模较小的问题,也即该问题能够分解成若干个子问题来解决.这是分治策略应用的前提,一般大多数问题都是可以满足的,这个特征充分反映了分治策略中递归思想的应用;
(3)若干个分解出的子问题的解能够合并为原问题的解;这一点是关键,能否利用分治法完全取决于问题是否具有第三条特征,如果具备了第一条和第二条特征,而不具备第三条特征,则可以考虑用贪心法或动态规划法;
(4)此问题分解得出的若干子问题必须是相互独立,即分解的子问题相互之间不存在公共的子子问题.这就涉及到分治策略的使用效率,如果各个子问题相互之间是不独立的,有共性部分,则分治法就要做许多重复的工作,公共的子问题被重复地解决,此时虽然可以使用分治算法,但其效率较低,这时反而使用动态规划算法较好.
2 分治算法解析
在使用分治策略算法解决问题时,一般分为三个步骤操作.第一步,划分问题:首先将要解决的复杂问题分解成若干个较简单的同类型的小问题.在问题划分时,可以采取递归策略,即把一个规模大的问题逐步分解到若干个规模较小的子问题,直至分解成可以很轻松的直接求出这些子问题的解;然后将这些子问题逐层一级一级的合并,直至返回到最上层,即可得出原问题的解.根据分治策略划分问题的原则,一般的,每层可划分成两个子问题,并且这两个子问题在规模差不多最好.在逆向合并求解时要根据问题而异,有些问题逐层递归分解完后就能得到原问题的解,而有些问题可能需要先逐层的进行合并,原问题的解才可能得到.第二步,递归求解:当子问题经过层层划分到足够小时,轻松求解出最小子问题的解.第三步,合并问题:将已解决的下层子问题的解再逐层向上合并,最终得到原问题的解答.由上所述,分治算法的设计过程如下图1所示.
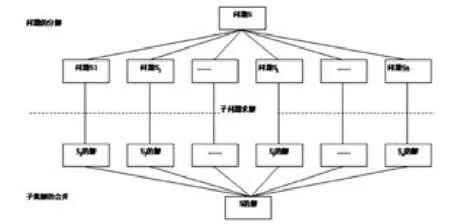
图1 分治算法设计过程
分治的框架结构如下:

3 分治策略在归并排序中的算法设计
在数据结构的排序算法中,归并排序效率较高.归并排序算法描述:通过将已经有序的若干个子序列合并,最后得出完全有序的序列.对一个没有排好序的序列进行排序,首先使用分割的方法先将大序列分割成一个个已排好序的小序列,利用归并的方法,再将排好序的子序列合并成一个完整的排好序的序列[2].以上正好符合分治策略的思想,在诸多的排序算法中,例如堆排序、归并排序、快速排序等等,都存在有分而治之的思想.而归并(Merge)排序算法是采用分治策略(Divide and Conquer)的典型的应用.下面以实例加以分析比较,问题描述如下:
3.1 已知某数列存储在序列A[1],A[2],……,A[n],拟采用分治策略对它们进行排序(从小到大或从大到小).
例如:10 4 6 3 8 2 5 7
排序后为:2 3 4 5 6 7 8 10
按照分治策略的三步法,对归并排序问题解决如下:
划分问题:把这组序列分成元素个数尽可能相等的两部分;
递归问题:把两半元素分别排序;
合并问题:把两个已有序的序列合并成一个序列.如图2所示.

图2 归并排序的分解与合并
划分问题与递归问题这两部分较易完成,关键在于第三步,如何把两个有序序列合并成一个有序序列.图3给出了一个合并的过程:把两个有序表中的最小元素加以比较后,选取其中的较小元素删除,并加入合并后的新表中,重复多次即可.

图3 归并排序合并的过程
归并算法如下:


3.2 归并排序的变形——求逆序对数目
给定一整数数组A=(A1,A2,…An),若i
分析本题,很容易想到一个非常简单的算法——穷举算法,即对数组中任意的两个数组元素进行分析判断,看它们能否构成“逆序对”.这种算法完全可行,但它的时间复杂度为O(N2).时间效率不尽如人意.

考虑采用分治求解:
·划分问题:把数组分成元素个数尽可能相等的两部分;
·递归求解:求解划分后的逆序对数目(i和j都在左边或者都在右边);
·合并问题:合并求解逆序对数目(i在左边但j在右边).
记数列a[L]~a[R]的逆序对数目为d(L,R);mid=(L+R)/2,则有:d(L,R)=d(L,mid)+d(mid+1,Rd)+F(L,mid,R).其中F(L,mid,R)表示一个数取自a[L,mid],另一个数取自a[mid+1,R]时所构成的逆序对数目.和上面介绍的归并排序一样,划分部分和递归求解部分都较简单,关键在于如何合并——怎样求出i在左边而j在右边的逆序对数目?统计的常见技巧是“分类”.首先按照j的不同对这些分布两边的逆序对进行分类:即对于右边的每个j,我们统计左边比它大的元素的个数f(j),然后将所有f(j)相加,其和即是答案.
以上的归并排序同时完成了f(j)的计算:因为最后的合并操作是从小到大进行排序的,也即当右边的a[j]复制到临时变量temp中时,左边还未复制到temp的那些数就是左边所有比a[j]大的数.此时的累加和中再加上左边元素个数mid-i+1即为答案.

在上例中,通过分析利用穷举算法和分治算法比较之,分治算法的优势显而易见.
4 小结
在各种排序算法中,如堆排序、归并排序、快速排序等,利用分治策略的归并排序效率较高.若数列长设为N,将大数列分解成若干小数列共需logN步,其中每步都是合并有序数列的过程,其时间复杂度为O(N),故一共为O(N*logN).由于归并排序每次操作均在相邻的数据中进行,所以归并排序在时间复杂度为O(N*logN)的几种排序算法中效率较高[3].
〔1〕吴文虎.程序设计基础[M].北京:清华大学出版社,2010.181-194.
〔2〕吴耀斌,曹利国,等.高级教程系列-信息学奥林匹克教程提高篇[M].湖南:湖南师范大学出版社,2013.213-229.
〔3〕李六杏.基于隐含条件挖掘的枚举算法优化[J].安徽科技学院学报,2013,27(6):66-69.
