奇完全数素因数的一个性质
2015-12-29付瑞琴,杨海
·数理科学·
奇完全数素因数的一个性质
付瑞琴1,2,杨海1,3
(1.陕西师范大学 数学与信息科学学院, 陕西 西安710119;2.西安石油大学 理学院, 陕西 西安710065;3.西安工程大学 理学院,陕西 西安710048)
摘要:利用高次Diophantine方程的结果讨论奇完全数素因数的性质。证明了:如果n是奇完全数,p是n素因数,r是p在n的标准分解式中的次数,则σ(n/pr)/pr≠qt其中σ(n/pr)是n/pr的约数和,q是奇素数,t是正奇数或者适合t≤6的正偶数。
关键词:奇完全数; 素因数; 高次Diophantine方程
收稿日期:2014-03-14
基金项目:国家自然科学基金资助项目(11226038 11371012);陕西省教育厅专项基金资助项目(14JK1311)
作者简介:付瑞琴,女,陕西府谷人,从事数论及其应用方面的研究。
通讯作者:杨海,男,陕西府谷人,博士后,副教授,从事数论及其应用方面的研究。
中图分类号:O156.1
A property of prime divisors of odd perfect numbers
FU Rui-qin1,2, YANG Hai1,3
(1.College of Mathematics and information Science, Shaanxi Normal University, Xi′an 710119, China;
2.School of Science, Xi′an Shiyou University, Xi′an 710065, China;
3.School of Science, Xi′an Polytechnic University, Xi′an 710048, China)
Abstract:Using some results on higher degree Diophantine equations, the properties of prime divisors of odd perfect numbers are discussed. If n is an odd perfect number, p is a prime divisor of n and r is the degree of p in the factorization of n, then the result σ(n/pr)/pr≠qt is proved, where σ(n/pr) is the sum of divisors of n/pr, q is an odd prime, t is either an odd positive integer or an even positive integer with t≤6.
Key words: odd perfect number; prime divisor; higher degree Diophantine equation
设N表示全体正整数的集合。对于正整数a,设σ(a)是a的所有约数之和。如果正整数n满足
σ(n)=2n,
(1)
则称n是完全数。长期以来,完全数的性质一直是数论中引人关注的研究课题,其中奇完全数的存在性是一个迄今远未解决的著名难题,目前只得到了奇完全数存在的若干条件(参阅文献[1]的问题B1及其参考文献)。
设n是奇完全数,p是n的素因数,r是p在n的标准分解式中的次数。此时显然有gcd(pr,n/pr)=1。由于从文献[2]的定理1.9.2可知σ(a)是积性函数,所以从(1)可得
(2)
又从文献[2]的定理1.9.1可知gcd(pr,σ(pr))=1,故从(2)可得pr|σ(n/pr),所以σ(n/pr)/pr是正整数。设

(3)
最近,M.Dris和F.Luca[3]证明了:对于奇完全数n的任一素因数p,都有
f(p)≠1,2,3,4或5,
(4)
陈凤娟和陈永高[4]在同样的题设下证明了
f(p)≠q,q2,q3,q4,qq′或q2q′。
(5)
其中q和q′是不同的奇素数。2013年K.A.Broughan,D.Delbourgo和Q.Zhou[5]利用不同的方法证明并改进了文献[4]的结论,同时给出f(p)的一个下界:f(p)≥315。2014年,陈凤娟和陈永高[6]进一步改进了文献[5]的结论,给出了有关f(p)不取更多值的情形,同时也提出一个相关的公开问题。
本文从求解Diophantine方程的思路出发,利用高次Diophantine方程的结果及初等分析方法证明了下面的定理。
定理1对于奇完全数n的任一素因数p,都有
f(p)≠qt。
(6)
其中q是奇素数,t是正奇数或者适合t≤6的正偶数。
显然,上述定理部分地改进了文献[4]中的结果(5)。
1若干引理
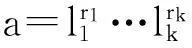

引理2[7]如果n是奇完全数,则n的标准分解式为
(7)
之形,其中π,p1,…,pk是不同的奇素数,s,s1,…,sk是正整数,而且π≡s≡1(mod4)。
引理3[8]如果n是奇完全数,则它的标准分解式(7)中的k≥8。
引理4[9]方程
X3+1=2Y2,X,Y∈N,X>1,
仅有(X,Y)=(23,78)。
引理5[10]方程
Xm+1=2Y2,X,Y,m∈N,X>1,m>3
无解(X,Y,m)。
引理6[11]方程
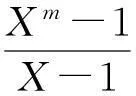
仅有解(X,Y,m)=(3,11,5)和(7,20,4)。
2定理1的证明
设n是奇完全数。从引理2可知n的标准分解式必为(7)之形,又从引理2可知

(8)
如果n的素因数p适合
f(p)=qt,t∈N。
(9)
其中q是奇素数,则从式(1),(2),(3)和(9)可知
(10)
p=π,r=s,
(11)
从式(7),(9)和(11)可知q必为p1,…,pk中的某数,所以不妨假定
q=pk,
(12)
因此,从式(7),(10),(11)和(12)可得
(13)
从式(13)可知
t≤2sk。
(14)
当s>1时,因为从引理2可知s≡1(mod 4),所以s≥5,(s+1)/2是适合(s+1)/2≥3的奇数。由于gcd(π(s+1)/2+1,(π(s+1)/2-1)/(π-1))=1而且π(s+1)/2+1是偶数,故从式(13)可得
(15)
或者

(16)

因为s=1,所以从式(13)可知

(17)
同时,从式(3),(7),(8),(9)和(12)可知
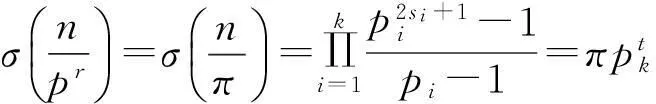
(18)
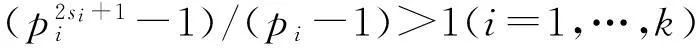
(19)
以及
(20)
其中ti(i=1,…,k-1)满足
t1+…+tk-1=t
(21)
如果t<2sk,则从式(17)可知
π≡-1(modpk)
(22)
又从式(19)可知
π≡1(modpk)
(23)
故从式(22)和(23)可得2≡0(modpk)这一矛盾。因此从式(14)可知
t=2sk,
(24)
从式(24)可知:当t奇数时,式(9)不可能成立。
另外,因为ti(i=1,…,k-1)都是正整数,故从式(21)可知
t≥k-1。
(25)
又从引理3可知k≥8,故从式(25)可得t≥7。由于从式(24)可知t是偶数,所以当t是适合t≤6的正偶数时,式(9)也不成立。定理证毕。
参考文献:
[1]GUYRK.UnsolvedProblemsinNumberTheory(thirdedition)[M].Beijing:SciencePress, 2007.
[2]华罗庚.数论导引[M].北京:科学出版社,1979.
[3]DRISM,LUCAF.Anoteonoddperfectnumbers[EB/OL].arxiv: 1103.1437v3[math.NT], 2012,http://arxiv.org/abs/1103.1437V5.
[4]CHENFJ,CHENYG.Onoddperfectnumbers[J].BullAustralMathSoc, 2012, 86(3):510-514.
[5]BROUGHANKA,DELBOURGOD,ZHOUQ.ImprovingtheChenandChenresultforoddperfectnumbers[J].Integers,2013, 13(A39): 1-8.
[6]CHENFJ,CHENYG.Ontheindexofanoddperfectnumber[J].ColloqMath, 2014, 136 (1): 41-49.
[7]DICKSONLE.HistoryoftheTheoryofNumbers,vol.i[M].Washington:CarnegieInstitution, 1919.
[8]NIELSENPP.Oddperfectnumbershaveatleastninedistinctprimefactors[J].MathComput, 2007, 76(260):2109-2126.
[9]VANDERWAALLRW.Onthediophantineequationsx2+x+1=3y2,x3-1=2y2andx3+1=2y2[J].SimonStevin, 1972/1973, 46(1): 39-51.
[10]BENNETTMA,SKINNERCM.TernarydiophantineequationsviaGaloisrepresentationsandmodularforms[J].CanadaJMath, 2004, 56(1): 23-54.

(编辑亢小玉)
