Novikov方程的对称群分析
2015-12-29黄晴,王丽真,刘俊荣等
·数理科学·
Novikov方程的对称群分析
黄晴1, 王丽真1, 刘俊荣1,高雯2
(1.西北大学 数学学院, 陕西 西安710127; 2.西北农林科技大学 理学院, 陕西 杨陵712100)
摘要:研究了Novikov方程的对称群分析问题,构造了方程所容许的李对称的优化系统,进行了对称约化,并得到了方程的大量的精确解。
关键词:Novikov方程; 李对称; 优化系统; 精确解
收稿日期:2014-04-02
基金项目:国家自然科学基金资助项目(11201371);陕西省教育厅专项科研基金资助项目(11JK0482);陕西省自然科学基金资助项目(2012JQ1013)
作者简介:黄晴,女,陕西子长人,西北大学副教授,从事偏微分方程研究。
中图分类号:O175.2
Group analysis of the Novikov equation
HUANG Qing1, WANG Li-zhen1, LIU Jun-rong1, GAO Wen2
(1.School of Mathematics, Northwest University, Xi′an 710127, China;
2.College of Science, Northwest A&F University, Yanglin 712100, China)
Abstract:In this paper, group analysis of the Novikov equation is performed. The one dimension optimal system of the Lie symmetries admitted by the equation in consideration is constructed. In addition, all exact solutions or the reduced equations corresponding to the optimal system are presented.
Key words: Novikov equation; Lie symmetry; optimal system; exact solution
本文研究Novikov方程[1]
ut-utxx+4u2ux-3uuxuxx-u2uxxx=0,
(1)
的对称约化和精确解构造问题,其中F为光滑的实值函数,u=u(t,x),ut=∂u/∂t,ux=∂u/∂x,uxx=∂2u/∂x2,uxxx=∂3u/∂x3,utxx=∂3u/∂t∂x2。Novikov方程是Camassa-Holm方程
ut-utxx+3uux-2uxuxx-uuxxx=0
的推广。自从它被提出以来,就得到了广泛的关注和研究,众多学者从各种角度研究了其解的存在性和适定性[2-3]。另外,文献[4]运用经典的李对称群分析方法,得到了Novikov方程的李点对称及五个点对称相应的群不变解。但是,没有构造方程(1)所有可能的群不变解。
这里我们首先应用优化系统理论,由Novikov方程所容许的李点对称构造其相应的十五维优化系统,并证明其最优性;再对方程进行对称约化,推导相应于优化系统中各个对称的约化常微分方程,并构造群不变解。
1优化系统
由微分方程对称群理论,方程(1)容许李对称
X=τ(t,x,u)∂t+ξ(t,x,u)∂x+
η(t,x,u)∂u
当且仅当
X(3)[ut-utxx+4u2ux-3uuxuxx-
u2uxxx]|ut-utxx+4u2ux-3uuxuxx-u2uxxx=0 =0。
其中X(3)为X的三阶延拓[5-7]。文献[4]中得到了方程(1)所容许的五维李代数。
定理1[4]Novikov方程容许五维李代数,其无穷小生成子为
X1=∂t, X2=∂x, X3=2t∂t-u∂u,
X4=e2x∂x+ue2x∂u, X5=-e-2x∂x+ue-2x∂u。
(2)
其中离散变换(t,x,u)→(t,-x,u)将李对称X4变换为X5。
由于无穷小生成子的任意线性组合也是无穷小生成子,容许非平凡李对称的微分方程将会容许无穷多个不同的对称子群。因此为了完全理解方程的不变解,一个重要且必须的任务就是寻找那些能够对应本质不同的解的子群。对称群中任意变换都能够把一个解映射为另一个解,所以我们只需寻找那些与变换无关的解,即互相不等价的解。这样优化系统的概念应运而生[5-7]。构造子群的优化系统等价于构造子代数的优化系统。对一维子代数而言,这种分类等价于伴随表示的轨道的分类,其基本方法就是取李代数的最一般的表达形式,并用各种不同的伴随变换作用于其上,使其形式得以最大程度的简化。这种使用伴随表示来分类群不变解的思想源于Ovsiannikov[7]。
Novikov方程的李代数(2)的非零交换关系为
[X1,X3]=2X1, [X2,X4]=2X4,
[X2,X5]=-2X5, [X4,X5]=4X2。
伴随表示由李级数
给出,其中[Xi,Xj]为李对称Xi,Xj的换位子,ε为参数。表1给出李代数(2)的伴随表示,其中第i行第j列的元素表示Ad(exp(εXi))Xj。

表1 李代数(2)的伴随表示
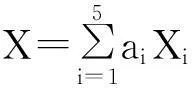
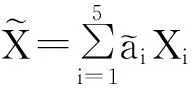
其中


4β2(a4+2a2α-4a5α2)。



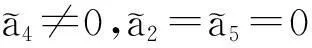

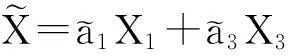
综合以上构造过程,得到下述定理。
定理2Novikov方程(1)所容许的李代数(2)的一维优化系统为
V1=X1, V2=X2, V3=X3,
V4=X4,V5=X2+X1,
V6=X2-X1, V7=X4+X3,
V8=X4-X3, V9=X4+X1,
(3)
V10=X4-X1, V11=X4-X5,
V12=X2+γX3, V13=X4-X5+X1,
V14=X4-X5-X1, V15=X4-X5+γX3。
其中γ∈R且γ≠0。
前面已经证明了式(2)的任意一维子空间等价于V1,V2,…,V15所张成的子空间,下面通过引入伴随不变量证明式(3)中的任意两个一维子代数相互不等价。

证 明易从表1观察知A=a3为李代数(2)的不变量。直接计算代数(2)的基灵型(killingform)可得
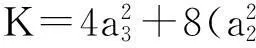

引理2定义函数
则C,D,E为不变量。
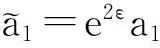
同理可证,D,E为不变量。
现在计算式(3)中所有Vi(i=1,2,…,15)的不变量A,B,C,D,E,结果列于表2。

表2 代数(3)的不变量
显然由表2可知,对于不同的i,或者相应于不同参数γ的相同的i,Vi(i=1,2,…,15)相互不等价,则定理2中优化系统(3)的优化性得以证明。
2精确解
前面我们构造了Novikov方程所容许的李对称群(2)的一维优化系统(3),这里利用统(3)来对Novikov方程作对称约化,得到用相似变量表示的约化常微分方程, 构造Novikov方程的精确解。需要指出的是,文献[3]中已经用V1,V2,V3,V4构造了Novikov方程相应的约化方程和不变解,这里我们仅考虑Vi(i=5,6,…,15)。
1)V5,V6=±∂t+∂x,其相似变量为z=x±t 和 u,对应精确解为
u=f(z)。
其中f(z)满足方程
(1∓f2)f ‴∓3ff ′f ″+(±4f2-1)f ′=0。
这两个约化方程无法找到通解,但均有形如c1ez+c2e-z的特解,这里以及下文中c1,c2均指任意实常数。
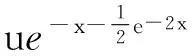

其中f(z)满足约化方程
(2f2-e-z)f ‴+(6ff ′+6f2-e-z)f ″+
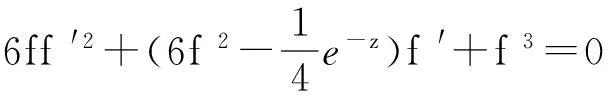


其中f(z)满足
(2f2+ez)f ‴+(6ff ′-6f2-ez)f ″-
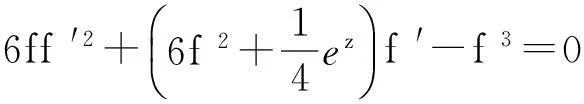
4)V9,V10=±∂t+e2x∂x+e2xu∂u,其相似变量为z=e-2x±2t 和ue-x,相应精确解为u=exf(z),其中f(z)满足方程
(f2∓1)f ‴+3ff ′f ″=0。
该约化方程有特解f(z)=z,即Novikov方程有解u=e-x±2tex。


4γ2(1-2γf2)f ‴+2γ2(1-12γff ′)f ″+


(f2∓1)f ‴+3ff ′f ″+(4f2∓1)f ′=0。
这两个约化方程均有特解f(z)=c1sinz+c2cosz,则Novikov方程有解
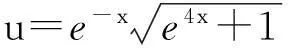
c2cos(2t∓arctane2x)]。

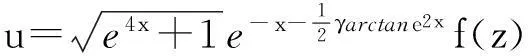
其中f(z)满足常微分方程
4γ2(1-2γe-zf2)f ‴+4γ2(-6γe-zff ′+
6γe-zf2-1)f ″+6γe-zff ′2+
(γ2-24γ3e-zf2-32γe-zf2+4)f ′+
4γ(γ2+4)e-zf3=0。
参考文献:
[1]NOVIKOV V. Generalizations of the Camassa-Holm equation [J]. J Phys A, 2009, 42: 342002.
[2]LAI S Y. Global weak solutions to the Novikov equation [J].J Funct Anal,2013, 265: 520-544.
[3]ZIMMERMAN W. Propagating fronts near a Lifshitz point [J]. Phys Rev Lett, 1991, 66:1546.
[4]BOZHKOV Y, FREIRE I L, IBRAGIMOV N H. Group analysis of the Novikov equation[J].Comp Appl Math,2013, DOI 10.1007/s40314-013-0055-1.
[5]IBRAGIMOV N H. Transformation Groups Applied to Mathematical Physics [M]. Dordrecht: Reidel, 1985: 96-159.
[6]OLVER P J. Applications of Lie Groups to Differential Equations [M]. New York: Springer, 1986: 66-96.
[7]OVSIANNIKOV L V. Group Analysis of Differential Equations [M]. New York: Academic, 1982: 162-219.
(编辑亢小玉)
