有源模拟滤波器的MATLAB辅助设计方法

丁宇，薛开昶，孙伟

(1.中国电子科技集团公司第十四研究所，江苏 南京 210039；2.国家精密微特电机工程技术研究中心，贵州 贵阳 550008)



有源模拟滤波器的MATLAB辅助设计方法

丁宇1，薛开昶2，孙伟1

(1.中国电子科技集团公司第十四研究所，江苏 南京 210039；2.国家精密微特电机工程技术研究中心，贵州 贵阳 550008)

摘要：在简要概述传统有源模拟滤波器设计方法的同时给出利用MATLAB进行有源模拟滤波器设计的方法，通过对有源模拟滤波器两种设计方法关键步骤的比较，给出了MATLAB能有效地简化有源模拟滤波器设计的结论。结合有源模拟滤波器的特性，给出了零极点分配原则和级联原则；同时介绍了如何用MATLAB给出滤波器总体和局部幅/相频特性，为滤波器调试提供了参考。通过设计实例，验证了本文提出的设计方案的便捷性、直观性、可行性。

关键词：模拟；有源；滤波器；MATLAB

0引言

有源模拟滤波器主要具有完成信号调理的功能，在计量测试领域，这种滤波器对于信号检测起着重要的作用。现阶段有源模拟滤波器传统的人工设计已比较成熟，但这种方式的设计过程复杂，计算量大。EDA(Electronic Design Automation)技术的不断发展，显著降低了模拟滤波器设计的难度和工作量。较为典型的模拟滤波器设计软件有Nuhertz公司的Filter Solutions，Schematica公司的Filter Wiz Pro，Linear公司的FilterCAD，Microchip公司的FilterLab。这些软件中Filter Solutions和Filter Wiz Pro功能较为齐全，但价格较为昂贵；FilterCAD和FilterLab是免费软件，但FilterCAD只能给出基于Linear公司生产器件的滤波器设计，而FilterLab的功能较为单一。

本文给出了一种基于MATLAB的有源模拟滤波器的设计方法，不需要查取滤波器的设计曲线及表格，并可查看所设计滤波器的频域特性，简化滤波器阶数、角频率和品质因数的计算过程。

1模拟滤波器设计方法

1.1　阶数确立

1.1.1传统方法

首先，计算滤波器的陡度系数Aslope；然后，对照归一化低通滤波器衰减特性曲线，找出一条阶数尽可能小但又能使其陡度超过Aslope的曲线，则这条曲线上的数字即为所设计滤波器需要的最小阶数n[1]。

由于确定滤波器阶数的衰减特性曲线以归一化的低通滤波器为标准，故陡度系数的计算过程包含将高通、带通和带阻滤波器向低通滤波器转化的归算，及将实际频率向单位频率的归算；低通、高通、带通或带阻滤波器需要采用不同的陡度计算公式。

1.1.2MATLAB辅助设计方法

在MATLAB软件下可以调用表1中函数计算滤波器的最小阶数n和截止角频率ωn。表1中的ωp和ωs表示通带和阻带角频率，单位为rad/s，Rp和Rs表示通带和阻带的纹波或衰减，单位为dB。对于低通、高通、带通和带阻滤波器，ωp和ωs的调用形式及约束条件如表2所示[2-5]。

表1　滤波器最小阶数求取函数

表2　ωp和ωs的调用形式及约束

本文中所说的传统设计和基于MATLAB的设计中求得的最小阶数n在低通和高通滤波器中为实际滤波器的阶数，在带通和带阻中为实际滤波器阶数的一半。原因是在低通到带通或带阻的变换中一对零极点将变换成两对零极点。这一点需要特别注意。

1.2　各级滤波器角频率及品质因数确定

1.2.1传统方法

首先，根据上一步得到的滤波器阶数n，查找归一化低通滤波器的极点；然后，将归一化低通滤波器极点去归一化，获取各级滤波器的参数[6]。去归一化过程包含低通向实际频率高通、带通和带阻滤波器转化的归算，及单位频率向实际频率的归算。当n为偶数时，设经查表得到归一化低通极点为-ai±jbi(i=1，2，…，n/2)；当n为奇数时，设经查表得到的归一化低通极点为-ai±jbi(i=1，2，…，(n-1)/2)和-a0。

对于带通滤波器，归一化低通至带阻转化时，一对低通复极点-ai±jbi对应两对带通复极点，一个低通实极点-a0转化为一对带通复极点，去归一化过程包括以下步骤：①计算带通滤波器的品质因数Qbp；②根据带通滤波器的品质因数Qbp，由一对低通复极点-ai±jbi计算两对带通复极点所对应的角频率ωbpi1，ωbpi2和品质因数Qbpi1，Qbpi2，由一个低通实极点-a0计算一对带通复极点对应的角频率ωbp0和品质因数Qbp0，ωbpi1和Qbpi1对应一节2阶带通滤波器电路，ωbpi2和Qbpi2对应一节2阶带通滤波器电路，ωbp0和Qbp0对应一节2阶带通滤波器电路。

对于带阻滤波器，归一化低通至带阻转化时，一对低通复极点-ai±jbi对应两对带阻复极点和虚零点，一个低通实极点-a0对应一对带阻复极点和虚零点；设一对低通复极点-ai±jbi对应的两对复极点角频率和品质因数为ωbri1，ωbri2和Qbri1，Qbri2，两对虚零点角频率为ωbr∞i1，ωbr∞i2；设一个低通实极点-a0对应的一对复极点角频率和品质因数为ωbr0和Qbr0，一对虚零点角频率为ωbr∞0。则去归一化过程包括以下步骤：①计算带阻滤波器的品质因数Qbr；②根据带阻滤波器的品质因数Qbr，由一对低通复极点-ai±jbi计算所对应的ωbri1，ωbri2，Qbri1，Qbri2，ωbr∞i1和ωbr∞i2，由一个实极点-a0计算对应的ωbr0，Qbr0和ωbr∞0。ωbri1，Qbri1和ωbr∞i1对应一节2阶带阻滤波器电路；ωbri2，Qbri2和ωbr∞i2对应一节2阶带阻滤波器电路；ωbr0，Qbr0和ωbr∞0对应一节2阶带阻滤波器电路。

1.2.2MATLAB辅助设计方法

在MATLAB下可以用表3中的函数根据上一步所确定的最小阶数n和截止角频率ωn计算出传递函数的零极点和分子分母多项式系数[2-5]，分别用于获取以下两种形式的传递函数：

(1)

(2)

表3中的‘ftype’在低通滤波器设计时用‘low’或省略，高通滤波器设计时用‘high’，带通滤波器设计时省略，带阻滤波器设计时用‘stop’。b和a分别为传递函数分子和分母系数；z，p和k分别为零点、极点和增益。

设由表3中函数求出的零极点为-ai±jbi。当bi=0时为实极点，当ai=0时为虚极点。此时零极点-ai±jbi所对应的1阶电路(对应实极点)或2阶电路的角频率ωi和品质因数Qi为

(3)

(4)

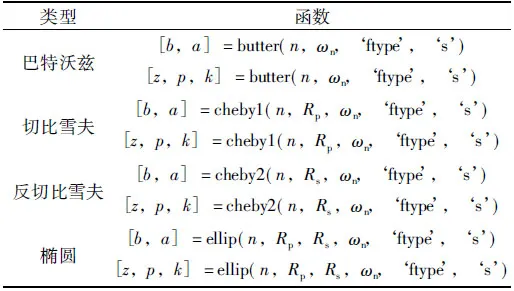
表3　零极点及传递函数求取函数

1.3　MATLAB在模拟滤波器中的优点

由上述比较可以看出，MATLAB在进行模拟滤波器设计时与传统方法相比具有以下优点：①不需要查表。在传统滤波器设计中，在阶数确定时需要对照响应曲线才能确定阶数，然而，对于不同的响应类型(巴特沃兹、切比雪夫等)和不同的通带纹波，就有不同的曲线，使得滤波器必须在使用滤波器设计手册的情况下才能进行设计。而采用MATLAB设计时可不用查表。②应用范围更广。采用MATLAB能设计一些传统滤波器设计手册中通常没有的响应类型(如反切比雪夫、椭圆等)和纹波值的滤波器。③设计更为简捷。由上述传统方法和采用MATLAB进行模拟滤波器设计的过程可以看出，MATLAB可以省去陡度系数求取、归一化、去归一化、零极点变换等一些传统方法必需的步骤，从而使设计更为简捷。

2滤波器设计时的几个关键点

2.1　零极图求取和零极点分配

在零极点或传递函数系数求出之后，可以用函数zplane(z，p)和zplane(b，a)查看滤波器的零极图。在含有零点的滤波器中，为实现动态范围的最大化和通带内损失最小化，零极点分配原则一般为：按极点对离虚轴的距离由近至远，依次选择离这对极点最近的零点与之匹配，直至零极点被完全匹配之后结束。这是由于同一节滤波器中的极点和零点相距越近，随着频率变化，滤波器传递函数中分母项和分子项的增益随频率变化的规律越一致，滤波器传递函数的增益随频率变化的规律越平缓。特别说明：当存在一个实极点时，与之相匹配的是处于原点的一个零点和一个无穷远处的零点；当零点个数少于极点个数时，采用添加无穷远处零点的方法，使零点和极点个数相等[7]。

2.2　级联顺序及增益分配

在多级1阶或2阶节级联时，由于输入信号中会含有高频噪声，第一节选择有低通或带通特性的节会使第一节之后的信号中含有的高频噪声被显著削弱，减小对后级滤波器的影响，故第一节一般优先选择有低通或带通特性的节；由于滤波器自身会产生频带较宽的噪声，当最后一节选择具有低通或带通特性的节时可以更好地限制滤波器自身产生的噪声频带，故最后一节一般优先选择具有低通或带通特性的节；同时，因为品质因数高的节比品质因数低的节具有更大的增益变化范围，故对于同一输入，当品质因数低的节在前面时，滤波器更不容易饱和，也不用对有用频带内的信号造成过度的衰减。因此，从前至后依次选择品质因数由低至高的节可以获得较高的动态范围[7]。

滤波器的增益的分配需要考虑各节滤波器的品质因数，一般应将高的增益分配到品质因数低的节上，这样能使滤波器实现更宽的动态范围，也可以通过折衷运放的增益和压摆率来实现降低滤波器中对运放的性能需求。但是由于定量的确定各级增益与品质因数的关系较为复杂，故工程上，一般把滤波器所需要的增益平均分到各节。这种增益分配方式得到的结果一般情况下不是最优的，但简单方便，已被广泛接受。

2.3　滤波器的响应分析

可以用函数ω=logspace(x，y，N)和freqs(b，a，ω)得到滤波器的幅频和相频特性。函数ω=logspace(x，y，N)表示一个以10x为起点，10y为终点，中间有N个对数等间隔点的向量。函数freqs(b，a，ω)则根据传递函数分子多项式系数b和分母多项式系数a，在角频率范围ω内绘制出滤波器的响应曲线[2-5]。当b和a为整体或局部某一节或几节传递函数的多项式系数时，则可以查看滤波器整体或局部的响应，为滤波器调试提供参考数据，从而降低滤波器调试难度。

3实验测试

假设需要设计一个带通滤波器，中心频率f0为1000 Hz，通带纹波Rp=0.5 dB，-3 dB带宽为50 Hz，在750 Hz和1250 Hz处衰减至少40 dB。则用MATLAB进行设计的步骤如下：

1)求取最小阶数。通过表3中函数[b，a] =ellip可得最小阶数n=2，另外ωn=[6126，6440] 。

2)求取零极点。通过函数[z，p，k] =ellip得到两对零点和两对极点分别为：z=±j4674.3，±j8440.6；p=-114.2±j6440.8，-108.6±j6123.7；k=0.01。

由上述零极点和增益分配原则，取第一个2阶节的参数为：z1=±j4674.3，p1=-108.6±j6123.7，k=0.1。第二个2阶节的参数为：z2=±j8440.6，p2=-114.2±j6440.8，k=0.1。

再根据零、极点与角频率、品质因数的关系，得第一节和第二节的参数分别为：ω1=6125 rad/s，Q1=28.2，ωr1=4674 rad/s；ω2=6442 rad/s，Q2=28.2，ωr2=8441 rad/s。

3)求幅/相频特性曲线。根据函数zp2tf及freqs可得如图1所示的整体幅频特性理论曲线。

4)确定电路参数。选取图2所示的电路[1]实现滤波器。第一节时开关S接在1处，第二节时开关S接在2处。电容C的取值由式(5)[8]确定，有

1≤100/f0C≤10

(5)

式中：C为电容，μF；f0为中心频率，Hz。因为f0=1 kHz，故可取C=0.1μF。由

R1=R4=Q/ωC

(6)

R2=R3=R1/Q

(7)

(8)

R6=kR7

(9)

联立式(6)~(9)式，可得表4中的各个参数值。表4中电容单位为μF，电阻单位为kΩ。

表4　滤波器参数表

实测电路幅频特性如图1中实测曲线所示。中心频率为1022 Hz，-3 dB带宽为987~1082 Hz，在频率低于750 Hz和高于1025 Hz范围内幅度衰减大于40 dB。实测曲线与理论曲线基本相符。

4结束语

通过传统方法与采用MATLAB辅助设计的方法相比较，证明了采用MATLAB进行模拟滤波器更为简捷。同时，通过实验结果验证了MATLAB设计模拟有源滤波器的方法是可行的，实测曲线与理论曲线相似。采用MATLAB进行模拟滤波器有较好的应用前景。

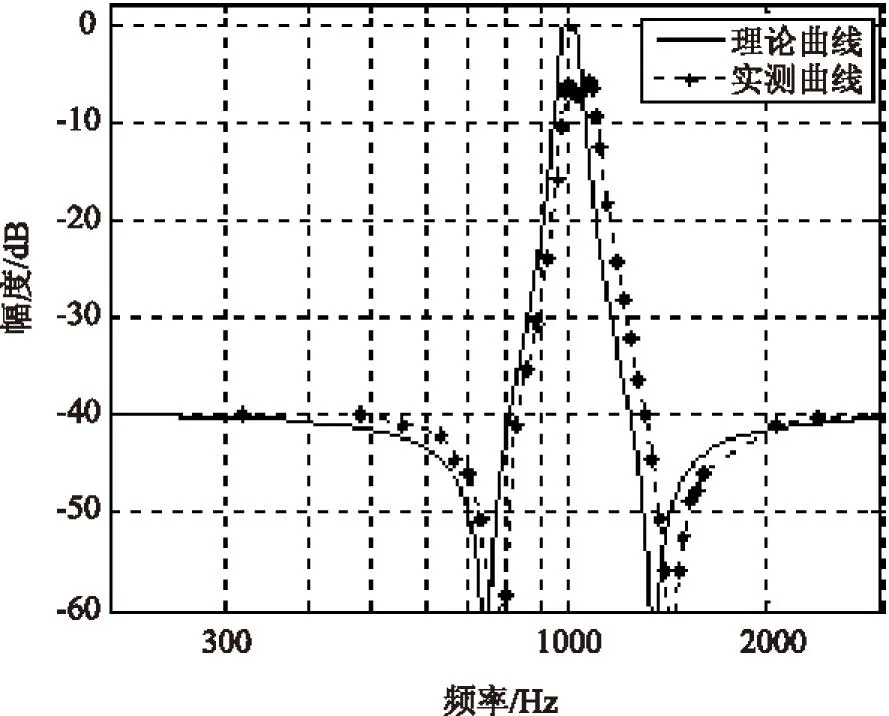
图1　滤波器整体幅频特性图

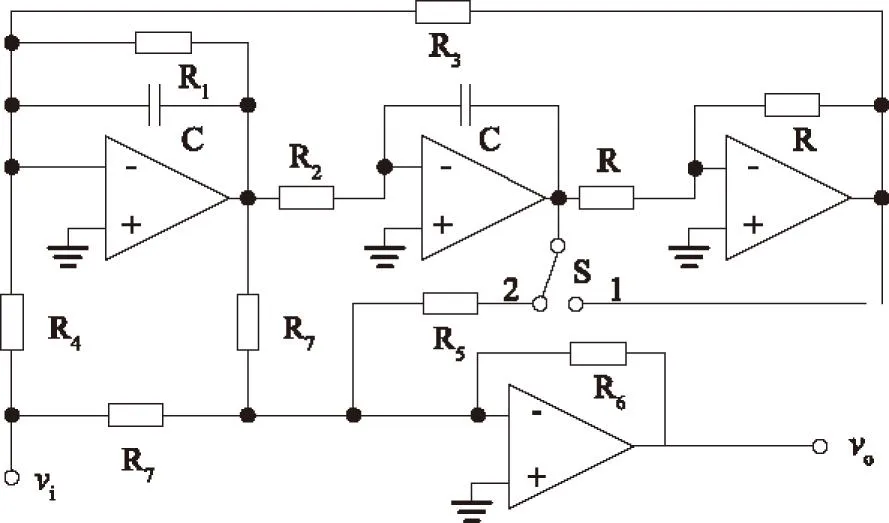
图2　滤波器电路图

参考文献

[1] Arthur B Willianms，Fred J Taylor.电子滤波器设计[M] .宁彦卿，姚金科，译.北京：科学出版社，2008.

[2] 赵开才.基于MATLAB的窄带模拟带通滤波器的快速设计[J] .自动化技术与应用，2014，33(5)：66-69，89.

[3] 林俊，黄炜.基于MATLAB的模拟滤波器设计实现[J] .电脑知识与技术，2008，4(1)：163-165.

[4] 肖有平，胡霞.高阶椭圆滤波器的设计与仿真[J] .电子测量技术，2007，30(3)：147-150.

[5] 史燕，杨小雪.基于Matlab和Multisim的综合性实验——椭圆滤波器设计与仿真[J] .北华航天工业学院学报，2008，18(S1)：21-22，25.

[6] Walt Jung.运算放大器应用技术手册[M] .张乐锋，张鼎，译.北京：人民邮电出版社，2009.

[7] 柳泽健，金光磐.有源滤波器的设计[M] .北京邮电学院数字通信专业.北京：人民邮电出版社，1978.

[8] Dauld E.Johnson，John L.Hilburn.有源滤波器的快速实用设计[M] .潘秋明，译.北京：人民邮电出版社，1980.

MATLAB-aid Design Method of Active Analog Filters

DING Yu1，XUE Kaichang2，SUN Wei1

(1.The 14th Research Institute，CETC，Nanjing 210039，China；

2.National Engineering Research Center for Small and Special Precision Motors，Guiyang 550008，China)

Abstract：The method of MATLAB-aid design of active analog filters is introduced after a briefly review of the traditional design method.By comparing the two methods on the key steps of active analog filter design，it is clearly showed that MATLAB can simplify the process of designing active analog filters.Based on the features of active analog filters，the rules of zero-pole distribution and cascading order are proposed.Simultaneously，the method of getting filter’s amplitude/phase vs.frequency character by MATLAB is introduced and it can offer a reference for debugging the filters.Through a certain example，the method proposed in this paper is proved to be simple，understandable and feasible.

Key words：analog；active；filter；MATLAB

作者简介：丁宇(1989-)，男，博士，研究方向为分析仪器研制；孙伟(1977-)，男，博士，研究方向为数字图像处理。

收稿日期：2015-07-13

中图分类号：TB535.2；TN713

文献标识码：A

文章编号：1674-5795(2015)05-0031-04

doi：10.11823/j.issn.1674-5795.2015.05.07