残周期正弦波形参数拟合及其应用

梁志国

(中航工业北京长城计量测试技术研究所 计量与校准技术重点实验室，北京 100095)



残周期正弦波形参数拟合及其应用

梁志国

(中航工业北京长城计量测试技术研究所 计量与校准技术重点实验室，北京 100095)

摘要：介绍了残周期正弦波拟合问题的难点及解决思想：以无需初始值预估计的模型拟合方式，化解残周期波形时信息不够全面的问题，从而一举解决了残周期条件下的正弦波形最小二乘拟合问题。针对残周期条件下的正弦拟合的特殊性，介绍了正弦波局域失真的思想及概念，以及适应于局域波形的噪声信号比的概念，并给出了噪声信号比对于正弦参数拟合误差的影响规律。针对残周期正弦波拟合的应用，给出了几个典型的应用事例，包括超低频正弦参数的快速估计、AM和FM信号波形的数字化解调、冲击波形峰值的精确估计、其它正弦波拟合算法的初始值估计等。证明了方法的有效性、可行性和工程实用价值。

关键词：计量学；正弦波；曲线拟合；参数估计；评价；残周期

0引言

正弦波形是人类应用最多且最广泛的波形之一，多种周期性的物理现象，诸如振动、摆动、波动、转动等，均可以展现出正弦波形特性，而人们广泛使用的交流电能、广播、电视、通讯、导航、仪器仪表等众多行业领域里均能见到正弦波的应用。因此，导致正弦波形的基本参数幅度、频率、初始相位、直流分量的估计和获取成为这些应用中最重要的基本工作之一。

关于正弦波形的四个参数，人们有众多的应用方式，而这四个波形参数的估计与获取，也有众多不同的方法[1-11]，如时域分析法、频域分析法、直方图统计分析法、最小二乘曲线拟合法、仿生非线性寻优法等。

这些方法各有千秋，多数情况下，均需要拥有多个周期的正弦波形才能进行有效的参数估计。当周期个数减少时，参数估计的准确度往往随之降低[12]，而当波形数目不足一个周期时，绝大多数估计方法均告失灵，无法有效给出所要估计的四个参数。然而，人们依然希望能够在不足一个周期的正弦波形条件下，有效估计出正弦波形的四个参数，这样的工作将在处理超低频信号参数快速估计，以及以正弦波为载波的调制信号解调等一系列场合具有重要的意义和价值。

1残周期正弦波形参数拟合

前已说明，有众多正弦参数估计方法，但当波形不足一个周期时，多数方法均失去了效用，其根本原因在于此时波形中的信息已经不全了，例如少于一个周期的信号波形直接导致周期信息(频率信息)不完整，由此导致直流分量信息不确切，进而峰峰值信息可能不完整，因而初始相位信息也可能不确切。

在这种情况下，最有可能获得有效估计结果的是曲线拟合法。理由是这种方法是直接使用正弦波模型作为拟合波形，通过寻找最小二乘意义下的残差有效值来确定拟合波形参数，因而可望在波形周期不完整的条件下仍然能够获得有效的估计结果。

有许多种最小二乘正弦波拟合法，它们自身依然需要在拟合中进行参数初始值的预估计[1-2]，当这些参数初始值距离真值目标较远时，极有可能导致估计过程发散，从而拟合失败。而在残周期条件下，波形参数的初始值估计恰是一个难点，在很多情况下都无法有效进行，因而参数估计本身很难确保实现。

文献[13] 找到一种方法，通过利用已知频率条件下的三参数拟合算法，将正弦波形的四个参数的非线性四维搜索寻优，转变成频率变量一个参数的线性搜索寻优，并给出了明确的收敛区间为(0，2πf0] ；其中，f0为信号的真实频率。无需初始值的预估计，将残周期正弦拟合参数估计变成现实。仿真拟合结果表明，使用该文所述方法，在最少至0.004个信号周期的波形数据已经可以正确拟合出正确的波形参数。当波形曲线含有约0.1个信号周期以后，拟合幅度与拟合频率趋于稳定和正常，当波形曲线含有约0.15个信号周期以后，拟合幅度与拟合频率将获得良好的拟合结果。

设正弦波形曲线方程为

y(t)=A0·cos(2πft+φ0)+D0

(1)

正弦波形采样序列为x1，x2，...，xn，其最小二乘拟合曲线为

(2)

ω=2πfΔt

拟合残差有效值为

(3)

式中：A为正弦波形的幅度拟合值；ω为正弦波形的角频率拟合值；φ为正弦波形的初始相位拟合值；D为正弦波形的直流分量拟合值；ρ为正弦波形的拟合残差有效值。而Δt为采样间隔。可以认为，在采样序列仅含有噪声误差时，ρ表示叠加在正弦波形之上的噪声实验标准偏差。

使用这种方法，在1/3个信号周期上执行波形最小二乘拟合，获得的拟合结果为：信号频率10.57349 Hz，幅度4773.703 mV，直流分量为-369.5314 mV，相位-0.31970 rad。拟合曲线与原始数据序列部分值如图1所示。用多个信号周期获得的拟合结果为：信号频率11.00287 Hz，幅度4459.356 mV，直流分量为42.254 mV，相位-0.317383 rad。其中，采集速率为2000 Samples/s，序列长度为1800点；信号幅度为4500 mV，频率为11 Hz。

图1　测量序列yi与拟合曲线(i)

2局域失真

引入残周期拟合方法后，如何评价拟合效果成为一个难点。其物理定义、应用价值、与现在正弦模型参量的关系问题等，均应相容。文献[14] 提出的局域失真的定义与概念恰好解决了这一问题。它在残周期局部波形拟合方法的基础上，推广丰富了正弦波形失真的定义与概念；将正弦波局域波形失真分解成“共模失真”、“差模失真”和“总失真”三部分，其中，当波形长度等于整数个周期时，局域总失真的定义与现有正弦波总失真的定义相一致，而差模失真和共模失真是总失真的两个不同的失真分量。

3残周期拟合效果的衡量

由于涉及到残周期正弦曲线拟合，造成以往的以完整波形为基础定义的波形参数在此产生了应用限制，无法确切描述拟合参数误差的变化规律。为此，文献[15] 提出了采样序列的噪声信号比的概念，并定义采样序列的噪声信号比为拟合残差有效值与波形序列最大值和最小值差异之比。并用该定义衡量残周期序列，找出了拟合参数误差与噪声信号比间的规律。

设正弦波幅度为5 V，频率1000 Hz，直流分量0 V，采样序列长度n=10000。

选取波形长度为0.4个信号周期，正弦波噪声信号比NSM=1%，初始相位φ0从0°~360°按照9°增量等间隔变化，获得采样序列噪声信号比NSR随初始相位φ0变化曲线如图2所示。

图2　NSR随初始相位φ0变化曲线

图3为幅度A、角频率ω和直流分量D拟合相对误差随初始相位φ0变化曲线，图4为初始相位φ0拟合误差随初始相位变化曲线。

图3　拟合相对误差随初始相位φ0变化曲线

图4　拟合相位误差Δφ随初始相位φ0变化曲线

4调制解调

由于能够在残周期条件下估计正弦波形的四个参数，并且良好的收敛性可保证在很宽的边界条件下的绝对收敛，因而该方法可以很容易地直接应用于AM，FM等调制信号的数字化解调[16-17]。除了拥有较强的自适应性外，由于残周期的适用性特征减小了解调的窗口效应，由此还获得了更高的解调分辨力和更好的响应特性。

图5为按照已知参数构造的理想调幅信号[16]，图6为其解调波形结果。其中，载波正弦波峰值1 V，频率100 Hz；调制信号为正弦波，调制度95%，频率为5.5 Hz；量程4 V，采样速率为8 kSample/s，n=5000。

图5　AM信号时域波形

图6　AM信号的解调波形结果

图7是使用Tektronix公司TDS784D型数字存储示波器，对于RS公司的SMT03型射频信号源的调频正弦信号进行测量获得的FM信号时域波形[17]；其A/D位数8，测量范围-4~4 V，采集速率25 MSample/s，采样点数n=5000；载波信号峰值1.414 V，载波频率300 kHz；调制频偏250 kHz，调制频率15 kHz。图8为FM信号的解调结果。

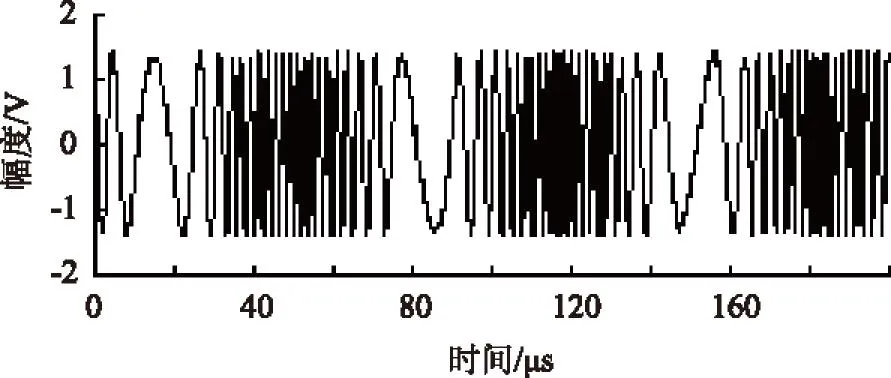
图7　实测FM信号时域波形

图8　FM信号的解调波形结果

5冲击波形峰值估计

有一些专业领域，本身研究的并非正弦波形，也可以尝试使用残周期正弦波拟合方式，并能获得良好的结果。例如，冲击专业中的基本任务——冲击峰值的估计，由于受到尖峰毛刺、振铃噪声、量化误差等因素的影响，在某些情况下很难获得精确的峰值估计结果，使用残周期正弦波曲线模型进行拟合处理，省去了滤波等环节，从原则上讲，应该能够获得更加精确的估计结果[18]。

用350B04型冲击加速度传感器(11024号)和配套的PCBF482A型放大器，在冲击加速度校准装置上按校准规范所述方法进行实验，获得如图9所示的冲击加速度校准曲线波形[19]。

图9　冲击加速度传感器校准曲线波形

所用采集设备为TDS544A型数字存储示波器。模拟带宽500 MHz，8 Bits A/D，最小电压分度1 mV/div，存储深度50 kSample/ch；双通道采样设置，每通道采样率为6.25 MS/s；放大器归一化系数为1，截止频率为30 kHz，放大倍数1。

该加速度传感器灵敏度的标称值0.9400 mV/g，用直接读取法获得其加速度校准脉冲峰值3221.14g，电压脉冲峰值为3.241 V，所用数字滤波器带宽20 kHz，按检定规程所述方法进行校准获得的校准灵敏度为1.0062 mV/g。

截取冲击波形峰值附近的约1/2幅度的脉冲，用残周期正弦参数拟合法进行波形拟合，获得拟合曲线与测量曲线的对比图如图10所示[18]，其正弦峰值拟合值为A= 0.7321408 V；直流偏移拟合值为D=2.675251 V；最终获得拟合脉冲峰值为 3.407392 V。此时，拟合残差的有效值为ρ=70.10334 mV。

图10　冲击加速度校准波形及拟合曲线(1/2幅度)

截取冲击波形峰值附近的约3/4幅度的脉冲，用残周期正弦参数拟合法进行波形拟合，获得拟合曲线与测量曲线的对比图如图11所示[18]，其正弦峰值拟合值为A=0.959759 V，直流偏移拟合值为D=2.422325 V；最终获得拟合脉冲峰值为3.382084 V。此时，拟合残差的有效值为ρ=91.8689 mV。

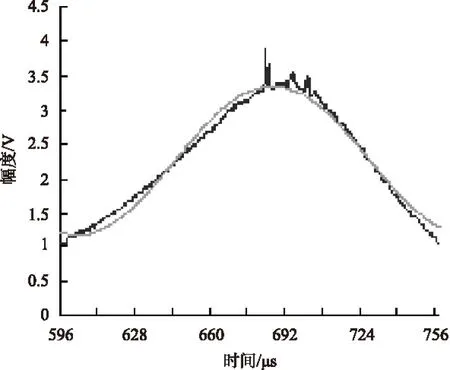
图11　冲击加速度校准波形及拟合曲线(3/4幅度)

6预估计

前已指明，有很多种最小二乘拟合算法都可以应用于正弦波形的参数估计，它们之所以不能应用于残周期条件下的正弦参数估计，主要是无法解决估计初始值的确定问题，当估计初始值可以确定以后，这些方法即可被唤醒，使用本文所述残周期最小二乘拟合算法获得的结果作为初始值，再结合牛顿法等其它四参数最小二乘拟合方法，可以获得更为精确的拟合结果。

由于在空间科学材料实验中针对热电偶信号的精度要求在微伏级，因而对系统的抗干扰能力有着很高的要求。在硬件设计中，通过放大调理电路的设计，系统接地方式的选取以及相应的抗干扰设计，从而减少噪声对系统的影响，提高信号检测精度[1]。

7结束语

综上所述可见，残周期正弦拟合方法出现后，不仅仅是对于正弦波形本身，例如超低频正弦参数的快速处理等，对于那些以正弦模型为基础的波形参数，如AM，FM信号的调制信号，以及单峰、单谷类冲击波形，S状波形等，很多种曲线波形都可以使用残周期正弦模型进行处理并获得一些波形参数信息。因而，对于波形参数的估计、处理和计量测试来说，具有广阔的应用前景和重大的实用价值。不仅如此，对于天体运行来说，多数情况下人们认为其是周期运行的，且周期可能非常长，远超出人的寿命本身，若能通过天体观测，以多普勒频移方式将其运行周期映射成正弦规律，则使用残周期正弦拟合方法本身推算和估计天体运行周期，在宇宙探索和天文研究中，将获得其它方法意想不到的效果，极大拓展人们的研究视野和研究空间，使一些原来不可能的事情变成可能。

参考文献

[1] John Kuffel，Terence R McComb，Ryszard Malewski.Comparative Evaluation of Computer Methods for Calculating the Best-Fit Sinusoid to the Digital Record of a High-Purity Sine Wave[J] .IEEE Transactions on Instrumentation and Measurement，1987，36(3)：418-422 .

[2] Terence R McComb，John Kuffel，Bryant C Le Roux.A Comparative Evaluation of Some Practical Algorithms Used in the Effective Bits Test of Waveform Recorders[J] .IEEE Transactions on Instrumentation and Measurement，1989，38(1)：37-42.

[3] Jeng Y C.High precision sinusoidal frequency estimator based on weighted least square method[J] .IEEE Transactions on Instrumentation and Measurement，1987，36(2)：124-127.

[4] Yih-Chyun Jenq，Philip B Crosby.Sinewave Parameter Estimation Algorithm with Application to Waveform Digitizer Effective Bits Measurement[J] .IEEE Transactions on Instrumentation and Measurement，1988，37(4)：529-532.

[5] Felice Cennamo，Pasquale Daponte，Mario Savastano.Dynamic Testing and Diagnostics of Signal Analyzers[J] .IEEE Transactions on Instrumentation and Measurement，1992，41(6)：840-844.

[6] Giaquninto N，Trotta A.Fast and accurate ADC testing via an enhanced sine wave fitting algorithm[J] .IEEE transactions on Instrumentation and Measurement，1997，46(4)：1020-1025.

[7] Dallet D，Slepicka D，Berthoumieu Y，et al.[ADC Characterization in Time Domain] Frequency Estimation to Linearize Time-Domain Analysis of A/D Converters[J] .IEEE Transactions on Instrumentation and Measurement，2006，55(5)：1536-1545.

[8] Zhang J Q，Zhao X M，Hu X，et al.Sine wave fit algorithm based on total least-squares method with application to ADC effective bits measurement[J] .IEEE transactions on Instrumentation and Measurement，1997，46(4)：1026-1030.

[9] 梁志国，张大治，孙璟宇，等，四参数正弦曲线拟合的快速算法[J] .计测技术，2006，26(1)：4-7.

[10] Peter Handel.Properties of the IEEE-STD-1057 Four-Parameter Sine Wave Fit Algorithm[J] .IEEE Transactions on Instrumentation and Measurement，2000，49(6)：1189-1193.

[11] 田社平，王坚，颜德田，等.基于遗传算法的正弦波信号参数提取方法[J] .计量技术，2005(5)：3-5.

[12] Deyst J P，Souders T M，Solomon O M.Bounds on least-squares four-parameter sine-fit errors due to harmonic distortion and noise[J] .IEEE Transactions on Instrumentation and Measurement，1995，44(3)：637-642.

[13] 梁志国，孟晓风.残周期正弦波形的四参数拟合[J] .计量学报，2009，30(3)：245-249.

[14] 梁志国，朱振宇，邵新慧，等.正弦波形局域失真及相变分析[J] .振动与冲击，2013，32(18)：179-182.

[15] 梁志国，武腾飞，张大鹏，等.残周期正弦波拟合中信噪比影响的实验研究[J] .计量学报，2013，34(5)：474-479.

[16] 梁志国，孙璟宇.调幅信号的数字化解调[J] .测控技术，2004，23(10)：17-20.

[17] 梁志国，孙璟宇.调频信号的数字化解调[J] .测试技术学报，2005，19(2)：190-194.

[18] 梁志国，李新良，朱振宇.一种基于残周期正弦拟合的冲击峰值计算方法[J] .振动与冲击，2015，34(1)：49-52.

[19] 国家质量监督检验检疫总局.JJF 1153-2006 冲击加速度计(绝对法)校准规范[S] .北京：中国计量出版社，2007.

Curve-fit Method and Its Application of Four-parameter Sine Wave with Partial Period

LIANG Zhiguo

(National Key Laboratory of Science and Technology on Metrology & Calibration，Changcheng Institute

of Metrology & Measurement，Beijing 100095，China)

Abstract：Both the difficulties and solving idea of four-parameter sinusoidal curve-fit with partial period waveforms are introduced in this paper，and through the method without pre-estimation of initial value of four-parameter，the problem of less information of partial period is solved.So the pre-estimation of four-parameter in sine wave curve-fitting is not needed.Aiming at the specialty of four-parameter curve-fit with partial period，a definition about the local distortion of sinusoidal waveforms is presented，and the definition of Signal to Noise Ratio of sampling series(SNR)and the Noise to Signal Ratio of sampling series(NSR)are put forward.By using the method of varying known parameters of partial period of sinusoidal waveforms and the Gauss noise level，when the width of period，phase，and SNR are varied，the varying rules of curve-fitting error of partial period sinusoidal are studied by experiments.The results show that，in partial period sinusoidal curve-fitting，the varying rule between NSR and phase of sinusoidal series is fixed，and all the curve-fitting errors of amplitude，frequency，phase，and DC bias vary as NSR.The partial period sinusoidal curve-fitting errors can be estimated by using simulation with curve-fitting parameters.In some experiments，including the fast parameter estimation of ultra-low frequency sine wave，the demodulation of AM，FM and PM waveforms，and the precise estimation of peak of impulse，and the initial value estimation of other sinusoidal wave forms curve-fitting，the validity and feasibility of the method are proved.

Key words：metrology；sinusoidal；curve-fit；parameter estimation；evaluation；partial period

作者简介：梁志国(1962-)，男，黑龙江巴彦人，研究员，博士，主要研究方向为数字化测量与校准、模式识别、动态校准、精确测量。

基金项目：航空科学基金资助项目(20085644009)

收稿日期：2015-07-03

中图分类号：TB973

文献标识码：A

文章编号：1674-5795(2015)05-0015-05

doi：10.11823/j.issn.1674-5795.2015.05.03