气体钻井高压条件下压缩因子计算方法探讨
2015-12-28符攀孟英峰刘星蒋勇
符攀 孟英峰 刘星 蒋勇
(1.西南石油大学油气藏地质及开发工程国家重点实验室,成都 610500;2.中石油云南昆明销售分公司,昆明 650000;3.中石化西南工程公司井下作业分公司,四川 德阳 618000)
采用气体钻井可较大幅度地提高机械钻速,节省钻井成本,有效防止井下复杂事故,降低油气层的损害,从而提高采收率的效果。随着深层油气藏勘探开发的深入,出现了越来越多的高压和超高压气井[1-2]。低压条件下气体钻井压缩因子计算模型并不适用于高压条件下气体钻井。目前国内外关于高压条件下压缩因子计算的主要方法有DAK法、HTP法、李相方法、张国东法。本次研究中通过mathcad程序针对上述方法进行计算,将计算结果与standing-katz超高压天然气偏差系数图版进行对比,拟优选出一种适合气体钻井高温高压条件下压缩因子计算模型。
1 低压模型
气体偏差因子反映的是实际气体状态偏离理想气体状态的程度,当压力低于35 MPa时,按下列式(1)计算:
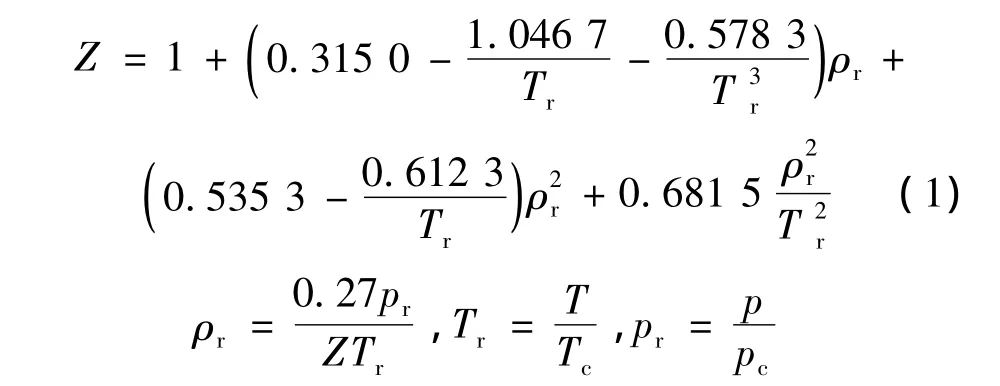
式中:Z—气体偏差因子,无量纲;
pr— 气体拟对比压力,无量纲;
Tr—气体拟对比温度,无量纲;
pc— 气体拟临界压力,MPa;
Tc— 气体拟临界温度,K。
运用mathcad软件编程,采用牛顿迭代法求解式(1),并与standing-katz超高压天然气偏差系数图版结果进行比较(表1)。
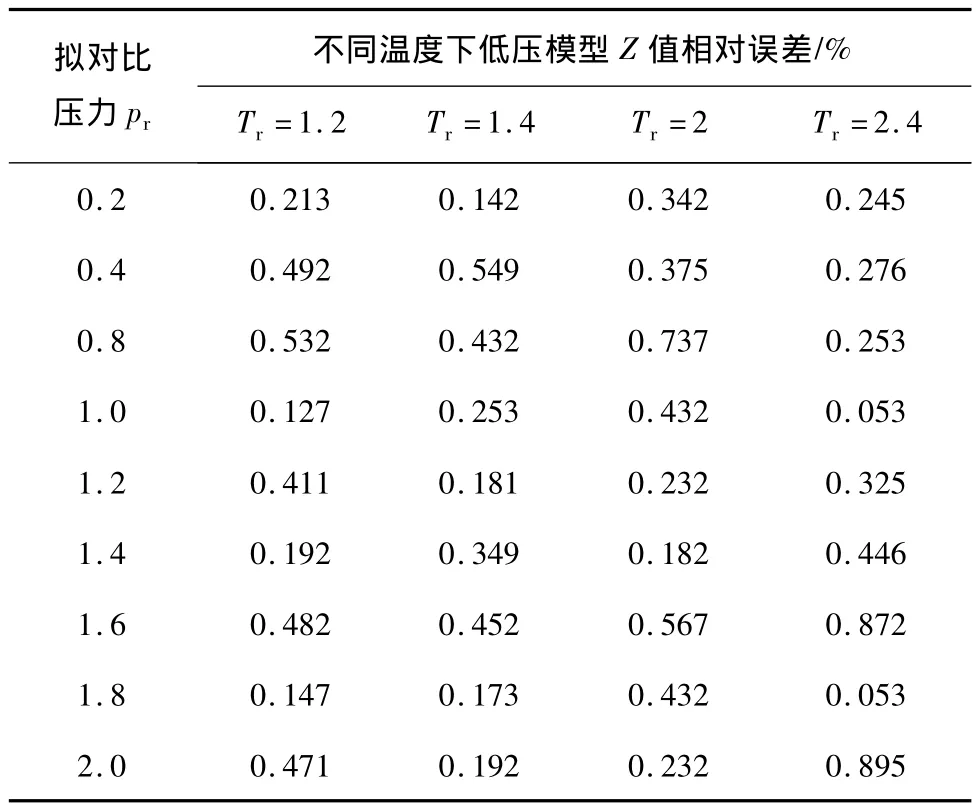
表1 低压模型不同拟对比温度下Z值计算误差分析结果
从表(1)可以得出,利用公式(1)计算低压段天然气压缩系数的精度非常高,计算数值与标准模板的吻合度也很高。
2 DAK模型
Dranchuk等人在1975年导出了计算气体对比密度的解析表达式,以用于估算天然气压缩因子[2]。对比气体密度表达式的定义,并通过非线性回归模型对standing-katz图版上的1 500个数据作拟合分析,得到具有11个参数的方程:
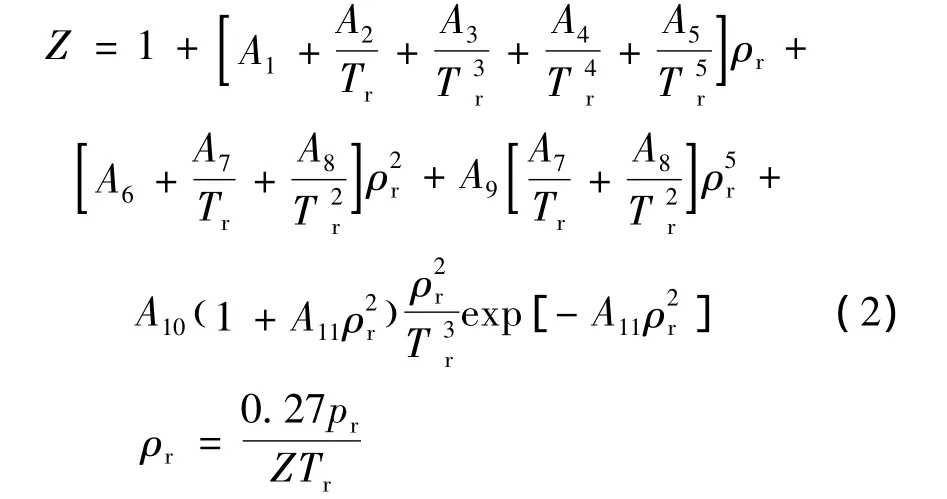
式中,A1~ A11为系数,分别为 0.326 5,-1.070 0,-0.533 9,0.015 7,-0.051 6,0.547 5,-0.736 1,0.184 4,0.105 6,0.613 4,0.721 0。式(2)的适用条件为 0.2≤pr≤15,1.0≤Tr≤3.0。
通过mathcad软件编程,运用牛顿迭代法求解式(2),并与standing-katz超高压天然气偏差系数结果进行比较(表2),绘制DAK模型压缩因子图(图1)。
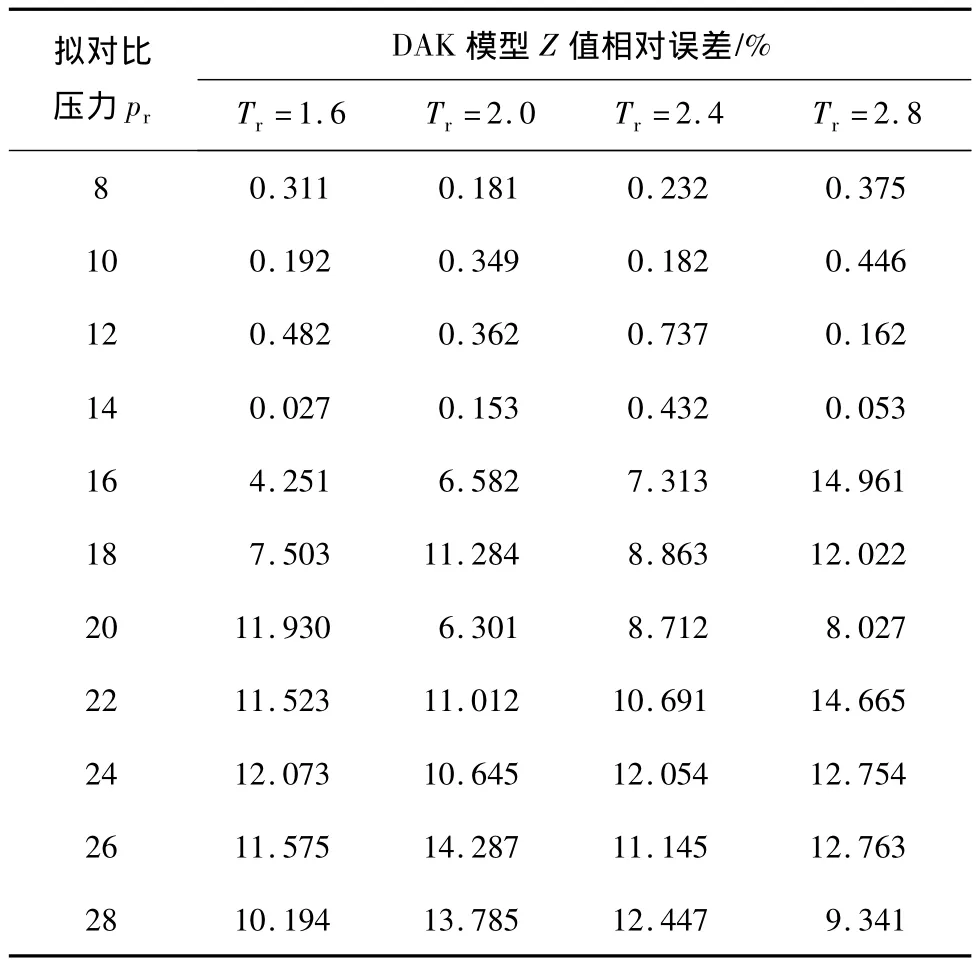
表2 DAK模型不同拟对比温度下Z值计算误差分析结果
当温度一定时,随着压力的升高,Z值逐渐增大;当压力一定时,Z值随着温度的升高而降低。从表2可以看出,当8<pr<14时,DAK模型计算精度非常高;当pr>10,DAK模型计算误差很大,且随着压力的增大,误差也越来越大。
3 LXF模型
李相方等人通过对standing-katz压缩因子图表的研究,发现压缩因子曲线在高压段呈直线趋势[3]。根据高压段的数据,采用多重高阶曲线拟合方法,拟合后的高压天然气偏差系数模型为:
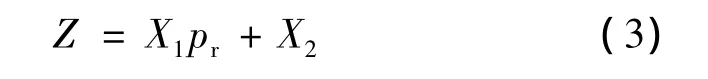
当8≤ pr< 15,1.0 < Tr< 3.0时,

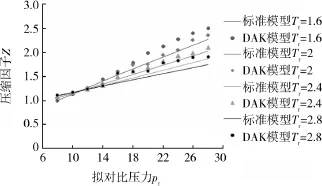
图1 DAK模型压缩因子图
通过编程将LXF方法计算结果与standingkatz超高压天然气偏差系数图版结果进行对比,对比结果如表3和图2所示。
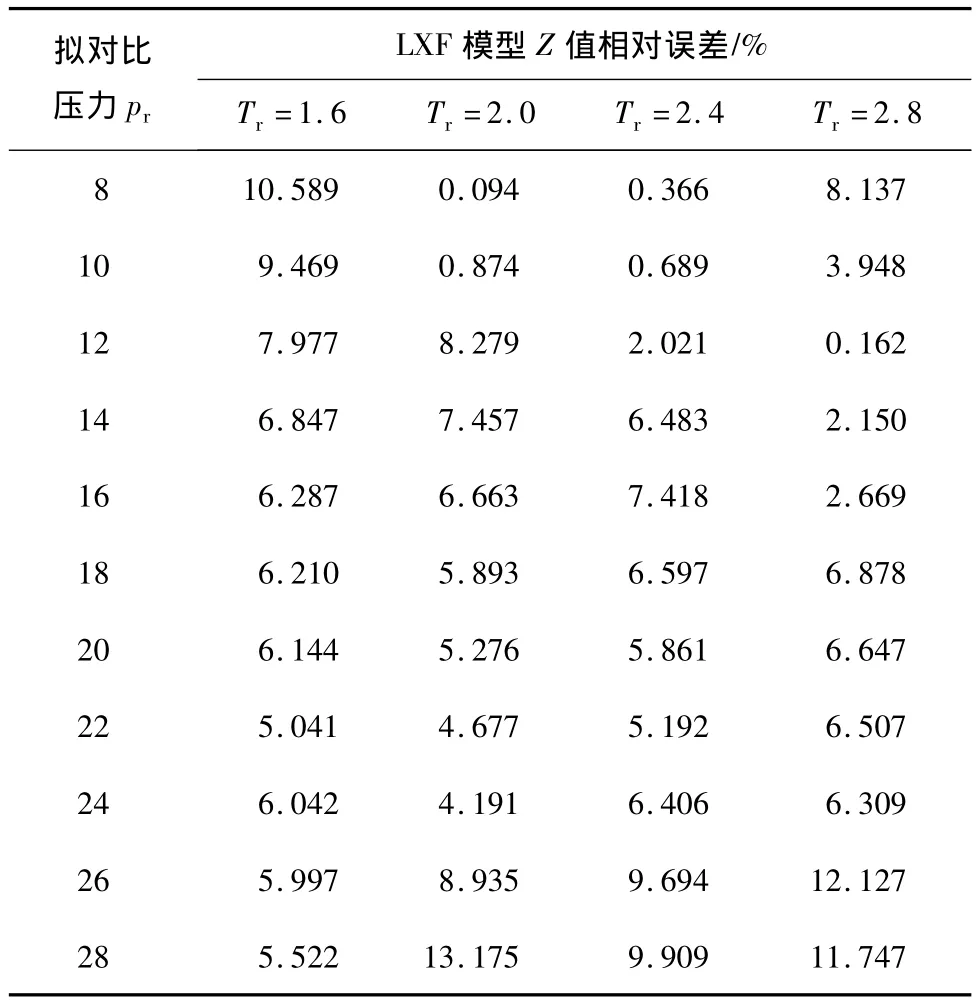
表3 LXF模型不同拟对比温度下Z值计算误差分析成果表
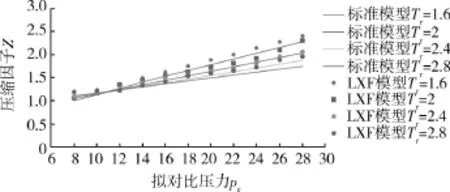
图2 LXF模型压缩因子Z对比图
由表3可以看出,LXF模型的计算精度较低。当2<Tr<2.4,8<pr<10时,LXF模型的计算误差很小,几乎为0,但是在其他温度和压力范围,LXF模型的误差很大。由此判断LXF模型的适用范围很小,不适合高温高压下压缩因子的计算。
4 Hall模型
Hall等人于1973年提出了一个准确描述Z因子的状态方程[4],方程中的系数由standing-ktaz图版数据拟合得出:

通过编程对Hall方法计算结果与standingkatz超高压天然气偏差系数图版结果进行对比,对比结果如表4和图3所示。
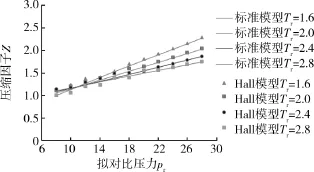
图3 Hall模型压缩因子图
由图3可以看出:当温度一定时,随着压力的升高,Z值逐渐增大;当压力一定时,Z值随着温度的升高而降低。这是因为当温度升高时分子间引力减小,从而使由于引力产生的压力变小。从表4可以看出:当8<pr<18时,Hall模型计算精度非常低,且随着压力的增大,误差变小;当pr>20时,Hall模型计算精度较高。
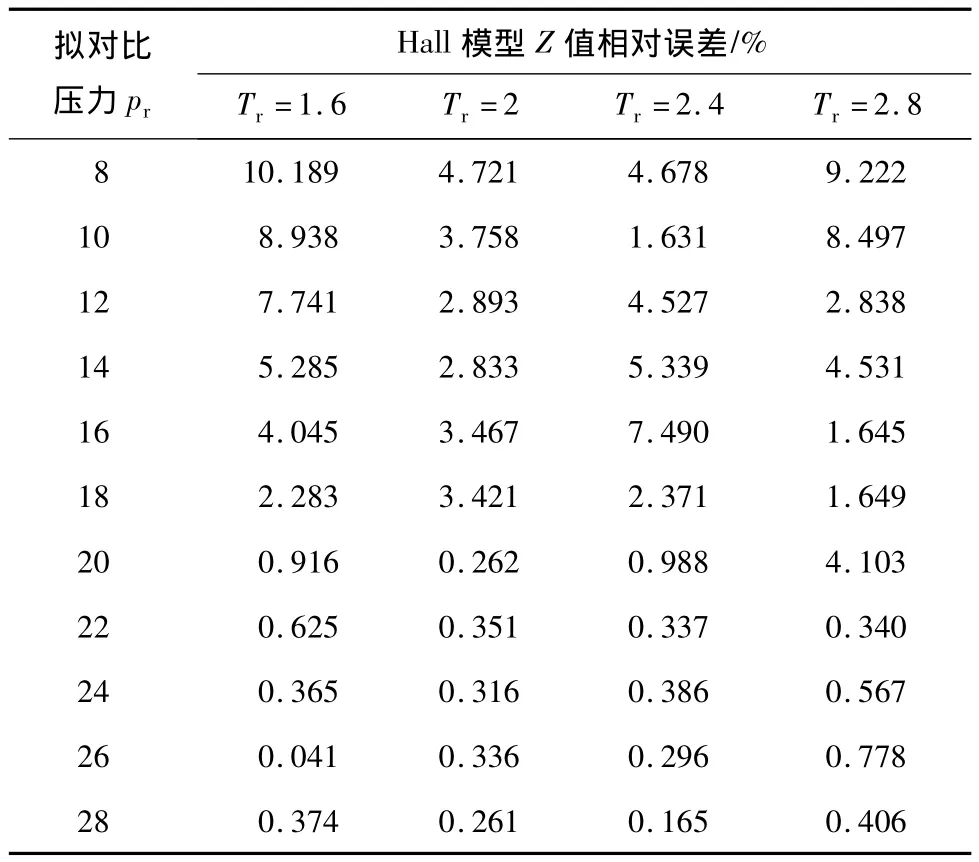
表4 Hall模型不同拟对比温度下Z值计算误差分析成果表
5 结语
通过对低压模型、DAK模型、LXF模型、Hall模型编程计算,并与standing-katz超高压天然气偏差系数图版结果进行对比得出:
(1)当pr<8时,低压模型计算精度较高;
(2)当8<pr<14时,LXF模型和Hall模型计算误差较大,而DAK模型的计算精度较高,因此在中压条件选用DAK模型进行压缩因子的计算;
(3)当pr>20时,Hall模型计算精度较高,LXF模型和DAK模型计算误差较大,因此,在高温高压条件选用Hall模型进行压缩因子的计算。
[1]阳建平,肖香姣,张峰,等.几种天然气偏差因子计算方法的适用性评价[J].天然气地球科学,2007,18(1):154-157.
[2]张国东,李敏,柏冬岭.高压超高压天然气偏差系数实用计算模型[J].天然气工业,2005,25(8):79-81.
[3]肖香姣,闫柯乐,王海应,等.一种预测超高压气藏压缩因子的新方法[J].天然气工业,2012,32(10):42-46.
[4]李相方,刚涛.高压天然气偏差系数的高精度解析模型[J].中国石油大学学报(自然科学版),2001,25(6):45-46.
[5]Hall K R,Yarborough L.A New Equation of State for Z-factor Calculations[J].Oil and Gas Journal,1973,71(25):82-92.
