基于整数规划模型的乘用车最优运输方案
2015-12-28周靖靖刘金杰张万里
周靖靖 刘金杰 张万里
(1.重庆师范大学经济与管理学院,重庆 401331;2.重庆师范大学数学学院,重庆 401331)
1 问题叙述
物流问题是近年来的研究热点之一。张腾松研究了整车物流配送路径的优化设计[1]。陈赛虎利用整数规划模型研究了轿车物流配载的优化问题[2]。秦绪伟等人研究了整车物流网络的集成优化问题[3]。本次研究主要解决2014年全国研究生数学建模竞赛提出的乘用车最优运输问题。具体问题背景如下:
双层轿运车又分为3种子型:上下层各装载1列乘用车,故记为1-1型;上层装载2列,下层装载1列,记为1-2型;上、下层各装载2列,记为2-2型,每辆轿运车可以装载乘用车6~27辆。
装载具体要求:每种轿运车上、下层装载区域均可视为长方形,各列乘用车均纵向摆放,相邻乘用车之间纵、横向安全车距均至少保持0.1 m,下层力争装满,上层两列力求对称,以保证轿运车行驶平稳。受层高限制,高度超过1.7 m的乘用车只能装在1-1型和1-2型的下层。乘用车、轿运车规格见表1和表2。
各因素关系:影响成本的要素首先是轿运车使用数量;其次,在轿运车使用数量相同的情况下,1-1型轿运车的使用成本较低,2-2型较高,1-2型略低于前两者的平均值,但物流公司1-2型轿运车拥有量小,为方便后续任务安排,每次1-2型轿运车使用量不超过1-1型轿运车使用量的20%;再次,在轿运车使用数量及型号均相同的情况下,行驶里程短的成本较低。

表2 轿运车规格 m
因为该物流公司是全国性公司,在各地均会有整车物流业务,所以轿运车到达目的地后原地待命,无须放空返回。每次卸车成本几乎可以忽略。
公司安排2次运输,在此需要制定详细计划,含所需各种类型轿运车的数量、每辆轿运车的乘用车装载方案。需要建立模型解决以下问题:
(1)最低成本下,物流公司运输Ⅰ车型的乘用车100辆及Ⅱ车型的乘用车68辆。
(2)最低成本下,物流公司运输Ⅱ车型的乘用车72辆及Ⅲ车型的乘用车52辆。
2 模型假设
(1)仅考虑双层轿运车型号;
(2)不考虑卸车成本;
(3)轿运车在运行过程中不会发生故障;
(4)轿运车到达目的地后原地待命,无须放空返回;
(5)各列乘用车均纵向摆放;
(6)假设各类轿运车的装载区域和乘用车均是长方形。
模型中各符号说明见表1。

表1 模型中各符号说明
3 模型建立及求解
为确定乘用车的最优运输方案,结合经典贪婪算法思想,在此给出改进的贪婪算法。算法主要步骤如下:
Step 1:输入乘用车的数量和类型,转Step 2;
Step 2:计算能够装载全部乘用车所需的轿运车型号及其最少数量,转Step 3;
Step 3:按每类轿运车装载后剩余空间最小为目标安排计算所需乘用车类型和数量转Step 4;
Step 4:计算具有相同装载方案的乘运车数量;并计算出每辆轿运车上层的装载方案;最后计算每类乘用车剩余数量,转Step 3;
Step 5:输出每辆轿运车的装载方案,结束。
3.1 问题(1)的模型建立及求解
3.1.1 确定最少轿运车车辆使用数
假设需要1-1型轿运车n1辆,1-2型轿运车n2辆,需要进行装载的Ⅰ车型乘用车有c1辆,Ⅱ车型乘用车有c2辆,则轿运车的使用数量越少越符合物流公司节约成本的要求[7],因此目标函数为min(n1+n2)。又由每次1-2型轿运车使用量不超过1-1型轿运车使用量的20%,故有n2≤20%n1。首先考虑1-1型轿运车与1-2型轿运车的下层宽度,w1和w2≤W1,w1和w2≤W2;再考虑1-2型轿运车的上层宽度:

将需要运输的乘用车全部纵向摆放,应满足在安全车距下其总长度小于轿运车运载长度之和。因此有:

建立以轿运车车辆数最少为目标的整数规划模型:

3.1.2 确定每辆轿运车的最优装载方案
(1)考虑每辆1-2型轿运车的乘用车装载方案。在此前已将1-2型轿运车上下层装载平面转化为3个长为L2的长方形,装载后剩下的空间长度min D1最少,即装载方案使得L2的长度充分利用。建立模型:
(模型1-2)min D1

其中k11为L2长度内所需Ⅰ型乘用车的数量,k12为L2长度内所需Ⅱ型乘用车的数量。
求得k11与k12后,计算需要安排的乘用车数量:
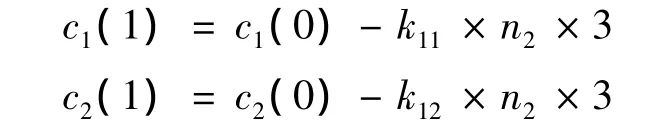
(2)考虑每辆1-1型轿运车的乘用车装载方案。前面已将装载平面转化为2个长为L1的长方形,由此建立装载后剩余空间长度最少的模型:
模型1-3 min D2
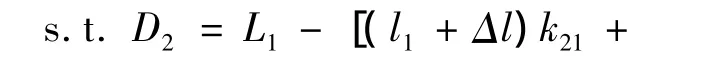
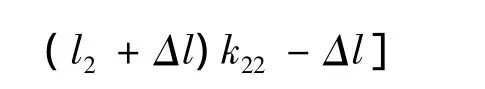
其中k21为L1长度内所需Ⅰ型乘用车的数量,k22为L1长度内所需Ⅱ型乘用车的数量。
求得k21与k22后计算剩余乘用车数量:
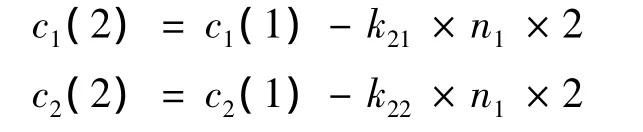
对c1(2)与c2(2)进行判断。若c1(2)与c2(2)大于0,则剩余c1(2)辆Ⅰ型乘用车和c2(2)辆Ⅱ型乘用车,此时则额外分配1辆1-1型轿运车运载;否则,若c1(2),c2(2)均小于等于0,则装配方案成立。
3.1.3 问题(1)的计算
令 c1(0)=100,c2(0)=60,使用 Matlab 7.11[6]软件编程计算可得问题(1)的最优装载方案如表3所示。

表3 Ⅰ车型(100辆)与Ⅱ车型(68辆)乘用车的最优运输方案
3.2 问题(2)的模型建立及求解
3.2.1 确定最少轿运车车辆使用数
设需要1-1型轿运车n1辆,1-2型轿运车n2辆,Ⅱ型乘用车有c2(0)辆,Ⅲ型乘用车有c3(0)辆,Δl为两车间隔。结合物流公司成本节约要求及车型限制,可建立以轿运车车辆数最少为目标的整数线性优化模型:
模型2-1 min(n1+n2)
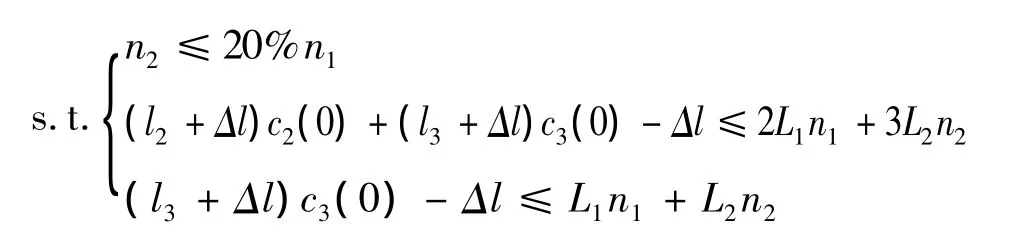
3.2.2 确定每辆轿运车的装载方案
(1)考虑每辆1-2型轿运车最佳运载方案。安排1-2型轿运车下层装载方案:设1-2型轿运车下层L2长度内可以安排k21辆Ⅱ型乘用车,k31辆Ⅲ型乘用车。
模型2-2 min D3

求得k21与k31后计算接下来需要安排的乘用车数量:
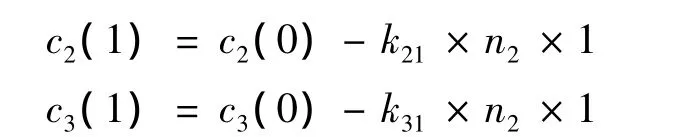
安排1-2型车上层装载方案。
模型2-3 min D32
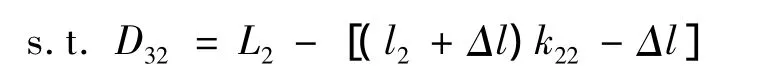
式中k22表示1-2型轿运车L2长度内装载的Ⅱ型乘用车数量。
计算安排完1-2型轿运车上下层后,乘用车的剩余数量:

(2)考虑每辆1-1型轿运车最佳运载方案。安排1-1型轿运车下层装载方案:设1-1型轿运车下层安排k23辆Ⅱ型乘用车,k32辆Ⅲ型乘用车,则有:
模型2-4 min D41
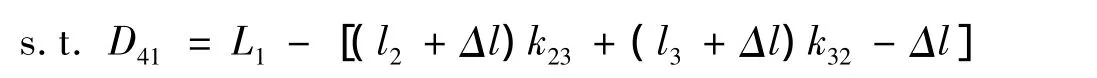
求得k23与k32后计算接下来需要安排的乘用车数量:
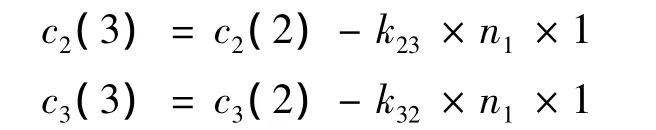
安排1-1型轿运车上层装载方案:设1-1型车上层安排k24辆Ⅱ型乘用车,则有:
模型2-5 min D42
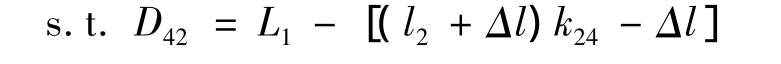
计算安排完1-1型轿运车上下层后乘用车的剩余数量:

对c2(4)和c3(4)进行判断:若c2(4)与c3(4)大于0,则剩余c2(4)辆Ⅱ型乘用车和c3(4)Ⅲ型乘用车,此时则额外分配1辆1-1型轿运车进行运载;否则,若c2(4)与c3(4)小于等于0,则装配方案成立。
3.2.3 问题(2)的求解
令c2(0)=72,c3(0)=52,用Matlab 7.11编程计算可得问题(2)的最优装载方案,见表4。

表4 Ⅱ车型(72辆)与Ⅲ车型(52辆)乘用车的最优运输方案
[1]张腾松.SQ公司整车物流配送路径优化研究[D].大连:大连海事大学,2012.
[2]陈赛虎.基于整数规划的轿车物流配载优化的研究[D].上海:上海交通大学,2008.
[3]秦绪伟,范玉顺,尹朝万.整车物流网络规划集成优化模型研究[J].计算机集成制造系统,2006,12(3):364-370.
[4]陈建岭.集装箱装载问题的启发式优化算法[J].山东交通学院学报,2006,13(3):53-56.
[5]何凤志,刘家财.安吉物流装车道位利用率优化设计[J].物流工程与管理,2014,36(5):107-109.
[6]张志涌,杨祖樱.MATLAB教程[M].北京:北京航空航天大学出版社,2006.
