简谐点荷载下饱和土中浮置板轨道隧道的动力响应研究

黄晓吉，扶名福，徐斌

(1．南昌大学建筑工程学院，江西南昌330031;2．华东交通大学土木建筑学院，江西南昌330013; 3．南昌工程学院土木工程系，江西南昌330099)

简谐点荷载下饱和土中浮置板轨道隧道的动力响应研究

黄晓吉1，2，扶名福1，徐斌3

(1．南昌大学建筑工程学院，江西南昌330031;2．华东交通大学土木建筑学院，江西南昌330013; 3．南昌工程学院土木工程系，江西南昌330099)

假定隧道衬砌为Flügge薄壁圆柱壳，土体为饱和多孔介质，通过把荷载、动力响应沿环向模态分解，利用傅里叶积分变换求得非轴对称简谐点荷载作用下的隧道—饱和土体系统的动力响应。在此基础上，将浮置板、钢轨作为无限长的Euler梁，考虑钢轨、浮置板、隧道—饱和土体系统的相互作用，求解了单层梁—隧道—饱和土体系统和双层梁—隧道—饱和土体系统在点荷载作用下的动力响应。研究结果表明:荷载频率对饱和土体中浮置板隧道的动力响应有较大影响;浮置板具有明显减振作用;在低频范围内，双层梁—隧道—饱和土体系统中上层的支承弹簧、钢轨的作用可以忽略。

简谐点荷载 浮置板轨道 隧道 饱和土体 动力响应

交通荷载作用下隧道系统的动力响应及其引起的安全和环境问题越来越受到关注［1-2］，国内外很多学者对该问题以及相应的减振降噪措施进行了研究［3-4］。浮置板式轨道结构是目前最有效的减振降噪措施之一［5-6］，因此在这个方面有不少研究文献。Cui等［6］将轨道和浮置板模拟为连续无限长梁，采用分层连续支承梁模型来研究浮置板轨道结构系统动力响应。Lombaert等［5］采用分层连续支承梁模型，考虑浮置板宽度的影响及与地基土的耦合作用，建立三维浮置板轨道结构模型研究其动力特性。马龙祥等［7］把钢轨作为点支承的无限长欧拉梁，浮置板作为不连续的点支承欧拉梁，依据周期结构的性质求得移动谐振荷载下浮置板轨道结构的动力响应。Hussein等［8］考虑了浮置板不连续性，将它视为周期性结构，并考虑该结构与车辆的耦合作用，研究了参数激励振动问题。李增光等［9］将钢轨简化为无限长欧拉梁，浮置板简化为不连续的Kirchhoff薄板，利用动柔度法分析了浮置板轨道结构的隔振性能。在浮置板轨道隧道的研究方面，Forrest和Hussein等［10-11］将隧道衬砌、外围弹性土体视为薄壁圆柱筒和无穷厚壁圆柱筒(pip模型)，把轨道和浮置板简化为连续支承的欧拉梁，分别建立单层梁和双层梁模型并考虑与隧道pip模型的耦合作用，计算了简谐点荷载下的动力响应;随后将两个钢轨视为不同荷载作用下的无限长欧拉梁，考虑浮置板与隧道衬砌水平方向和转动方向的耦合作用，计算了简谐荷载下整个系统的动力响应。国内孙成龙等［12］对北京地铁5号线灯市口站—东四站区间钢弹簧浮置板轨道的减振效果进行了测试与分析。韦凯等［13］基于车辆—轨道耦合作用，建立钢弹簧浮置板隧道—建筑物—地基二维有限元模型，计算合建结构的动力响应，分析钢弹簧浮置板的减震性能。

浮置板轨道结构的研究成果虽不少，但对其在饱和土体中隧道内的应用研究极少。本文在已有研究的基础上，将衬砌模拟为薄壁圆柱壳，在单位简谐点荷载下隧道—饱和土体系统动力响应的基础上，将浮置板和轨道均视为无限长连续支承的欧拉梁，建立单层梁—隧道—饱和土体模型和双层梁—隧道—饱和土体模型，分析简谐点荷载作用下饱和土体中两种浮置板隧道系统的动力响应。

1 隧道—饱和土体系统的动力响应求解

当荷载作用在圆形隧道仰拱内表面，隧道与饱和土体相互作用，构成隧道—饱和土体系统。

1.1 薄壁圆柱壳的控制方程及其求解

将隧道衬砌视为薄壁圆柱壳，其振动方程采用Flügge理论表示的方程。在θ=0，x=0仰拱处的简谐点荷载F=eiωt作用下，将隧道衬砌位移沿着环向模态进行分解后求和

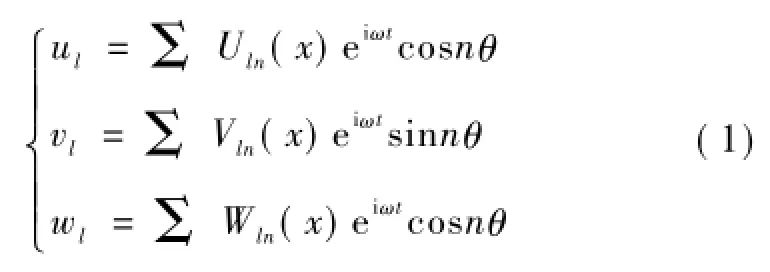
式中:ul，vl，wl分别为衬砌的轴向、切向和径向位移; Uln(x)，Vln(x)，Wln(x)分别为第n阶环向模态下三个方向的位移幅值。将式(1)代入薄壁圆柱壳的振动方程中并进行x→ξ的傅里叶积分变换，求得波数域内位移幅值表示如下

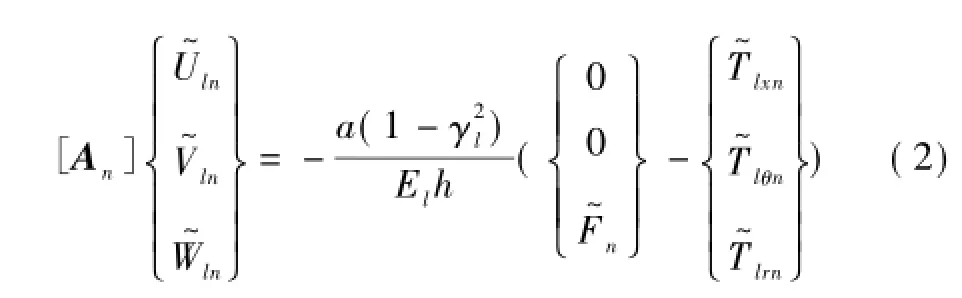
式中:An为波数域内第n阶环向模态的位移系数矩阵为荷载强度幅值，取为

1.2 饱和土体的控制方程及其求解

饱和土体的控制方程采用Biot方程，引入Helmholtz势函数使运动方程解耦。在简谐点荷载作用下，柱坐标下的土体骨架和孔隙水的势函数均表示为如下形式

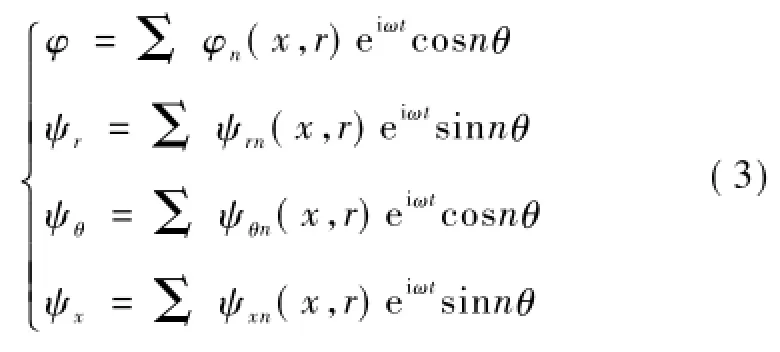
式中:φ，ψr，ψθ，ψx分别是土体或孔隙水的标量势函数和三个方向的矢量势函数;φn，ψrn，ψθn，ψxn分别为第n阶模态下的势函数幅值。

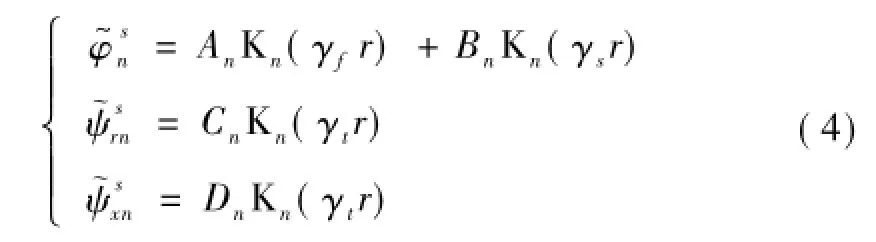
将式(3)代入Biot理论的运动方程式并对其进行x→ξ的傅里叶积分变换。结合辐射条件可求得第n阶模态下波数域内的土体骨架势函数式中:An，Bn，Cn，Dn是第n阶模态的待定常数;γf，γs，γt为饱和土中P1，P2和S波相对应的系数，且满足Im (γf)＜0，Im(γs)＜0，Im(γt)＜0;Kn()为第二类n阶修正Bessel函数。

利用矢量势函数的正则条件可求得土体骨架的另外一个矢量势函数

1.3 连续条件和边界条件

若隧道衬砌与饱和土体紧密接触，则波数域内r =a处第n个模态下两者三个方向的位移和应力连续(此处要注意的是薄壁圆柱壳和饱和土体位移、应力的坐标轴方向不一致)，即

在饱和土体与衬砌的接触面处(r=a)，若隧道衬砌完全透水，则土体中孔隙水压

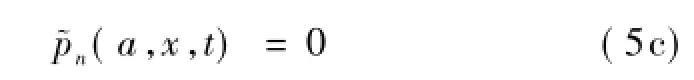
2 饱和土体中浮置板隧道系统的动力响应求解

2.1 单层梁—隧道—饱和土体系统的响应求解

在浮置板轨道隧道中，荷载F=eiωt作用在浮置板x=0处，经支承弹簧传递到隧道衬砌和外围饱和土体，如图1所示。将浮置板模拟为连续支承的无限长Euler梁，考虑浮置板与隧道—饱和土体系统的相互作用，建立单层梁—隧道—饱和土体系统。

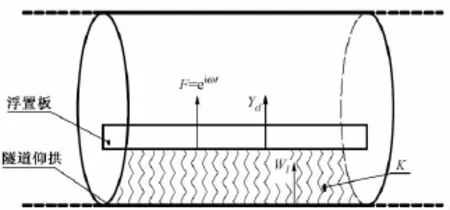
图1 饱和土中单层梁浮置板隧道的计算简图

由于浮置板与隧道仰拱的相互作用，作用在衬砌仰拱内表面的荷载为分布力q=q(x)eiωt而不再是点荷载F=eiωt，如图2所示。为波数域内浮置板底的接触反力;md和EdId分别是浮置板的线密度和抗弯刚度。

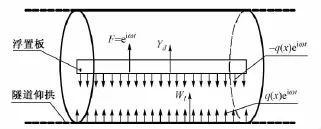
图2 浮置板与隧道仰拱之间的相互作用力

由于作用在隧道仰拱的荷载不再是点荷载而是分布力q(x)eiωt，浮置板隧道系统中衬砌和外围饱和土体的动力响应变为Y(x)。由文献［10］可知，波数域内衬砌和外围土体的动力响应可根据Duhamel积分和卷积积分公式求得，如下式

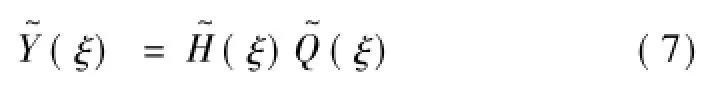
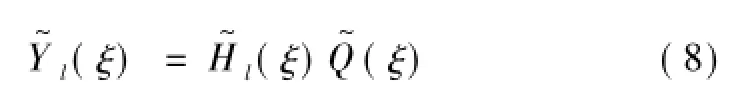
从式(6)—式(8)可知在单层梁—隧道—饱和土体系统中动力响应求解的关键在于波数域内浮置板底的接触反力为此根据浮置板支承弹簧的受力条件求解得

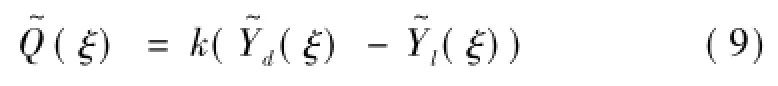
式中，k为浮置板支承弹簧的刚度。

联立式(6)、式(8)、式(9)可以求得浮置板底接触反力，从而求得单层梁—隧道—饱和土体系统的动力响应。

2.2 双层梁—隧道—饱和土体系统的响应求解

若将钢轨视为连续支承的无限长Euler梁，且钢轨在x=0处作用着简谐点荷载F=eiωt，如图3所示。考虑钢轨、浮置板与隧道—饱和土体系统的相互作用，建立双层梁—隧道—饱和土体系统。

钢轨上面的荷载包括x=0处的简谐点荷载F= eiωt和钢轨底部接触反力－q'(x)eiωt，则波数域内钢轨的位移幅值

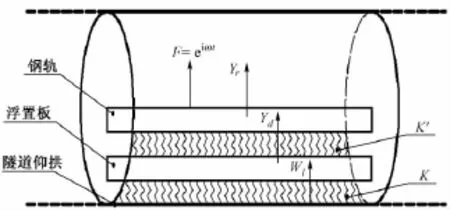
图3 饱和土中双层梁浮置板隧道的计算简图

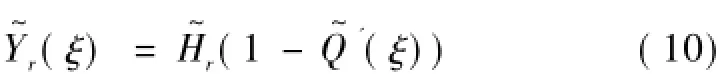
在双层梁—隧道—饱和土体系统中，浮置板上的荷载包括钢轨传递过来的分布荷载q'(x)eiωt和底部接触反力－q(x)eiωt，因此波数域内浮置板位移幅值为

浮置板上的荷载包括x=0处的单位简谐荷载F =eiωt和底部接触反力－q(x)eiωt，则波数域内浮置板的位移幅值为

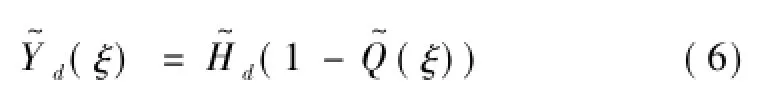
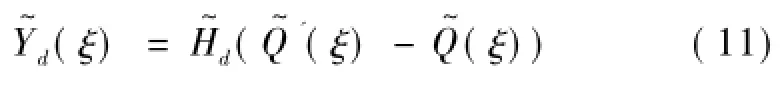
波数域内的分布荷载Q～'(ξ)可有上层支承弹簧的受力条件求解，即

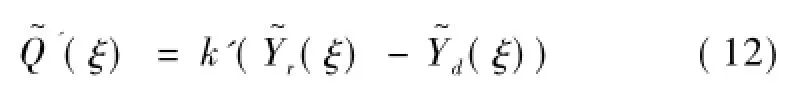
式中，k'为钢轨支承弹簧的刚度。

联立方程式(9)—式(12)，可求得双层梁—隧道—饱和土体系统中两个分布力Q～'(ξ)和Q～ξ，从而求得双层梁—隧道—饱和土体系统中的动力响应。

3 饱和土中两种浮置板隧道系统的算例分析

在x=0处单位竖向简谐点荷载作用下饱和土中有两种浮置板隧道系统，一为单层梁—隧道—饱和土体系统，另外一个为双层梁—隧道—饱和土体系统。为便于比较计算结果，除孔隙水的参数外，土体骨架、隧道衬砌参数、浮置板的抗弯刚度和线密度、钢轨的抗弯刚度和线密度、钢轨支承弹簧的刚度和阻尼系数取自文献［10］，在此不一一列举。浮置板支承弹簧刚度k0=424.4×106N/m2，阻尼系数η=0.5(同文献［10］中的一个工况)。两个Euler梁的支承弹簧刚度均采用考虑阻尼的复刚度形式k=k0(1+iη)。孔隙水的密度ρf=1 000 kg/m3，孔隙率f=0.3，系数α=0.97，水的弯曲系数a∞=2.0，系数M=2.4×108N/m2，土体骨架与孔隙水间的相互作用力参数bp=2.0×107kg/(m3·s)。

当饱和土体的参数ρf，α，M，bp，f，a∞接近于0时，饱和土体中浮置板隧道系统可退化成文献［10］弹性土体中的浮置板隧道。为检验本文方法与程序的正确性，本文首先计算了简谐点荷载作用下弹性土体中单层梁浮置板隧道系统x=θ=0的仰拱处径向位移幅值、浮置板的竖向位移幅值，随后计算了饱和土体中两种浮置板隧道系统的动力响应。在动力响应计算过程中，共取前面11阶(0～10)模态计算，傅里叶积分变换采用的样本点数N=2 049，空间间隔Δx=0.5 m (同文献［10］)。

图4为三种浮置板隧道系统中浮置板的竖向位移幅值随荷载频率的变化曲线。文献［10］的弹性土体中单层梁隧道系统浮置板的竖向位移幅值与本文计算的单层梁—隧道—弹性土体系统中相应的位移幅值基本一致，验证了本文方法与程序是正确的。弹性土体单层梁—隧道系统中的浮置板位移首先随着频率增加而增大，由文献［10］可知，在荷载频率为45 Hz时，浮置板的位移幅值达到最大值，而后逐渐减小。然而饱和土体中两种隧道系统的浮置板位移在频率为50 Hz左右达到最大值。当荷载为＜50 Hz的低频荷载时，饱和土体两种隧道系统中浮置板的竖向位移幅值几乎相同并且小于单层梁—隧道—弹性土体系统的位移幅值。然而当荷载频率＞50 Hz，弹性土体中单层梁隧道系统的浮置板位移与饱和土体中单层梁隧道系统浮置板的位移几乎重合，双层梁—隧道—饱和土体系统中浮置板的位移大于两个单层梁浮置板隧道系统中浮置板的位移。

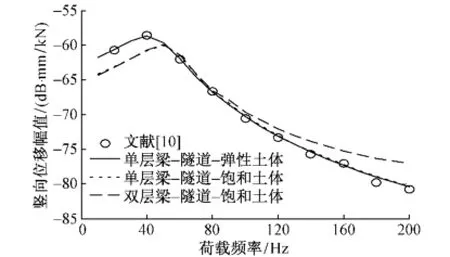
图4 浮置板荷载点处竖向位移幅值随荷载频率的变化曲线

图5为四种隧道系统仰拱x=0处的径向位移幅值变化曲线。可知，本文计算的单层梁—隧道—弹性土体系统仰拱处的径向位移幅值与文献［10］几乎完全相同，再次证明了本文方法与程序的正确性。与浮置板的位移类似，饱和土体中两种隧道系统仰拱处的径向位移幅值均在50 Hz左右达到最大，而后逐渐减小。饱和土中单层梁隧道系统和双层梁隧道系统的浮置板对仰拱均具有明显的减振作用，与隧道—饱和土体系统相比，饱和土中两种浮置板隧道的径向位移幅值小很多。与浮置板的位移类似，当荷载频率较低时，饱和土中两种浮置板隧道系统仰拱处的径向位移幅值几乎重合，而从80 Hz左右开始，双层梁—隧道—饱和土体系统仰拱处的径向位移幅值大于单层梁—隧道—饱和土体系统的径向位移。这是因为双层梁的浮置板隧道系统中，由于有双层弹簧，相当于减小了整个隧道系统的刚度，导致位移增大，但是这种刚度减小带来的影响只有在较高频率的荷载作用下才会显现。

图6为饱和土体中三种隧道系统外围土体r=3.5 m，x=0，θ=0处径向位移幅值的变化曲线。当荷载频率低于50 Hz时，浮置板隧道对土体的减振作用基本上可以忽略;当荷载频率高于50 Hz时，浮置板隧道对外围饱和土体位移幅值的减振作用随着频率的增加明显增大。当荷载频率高于100 Hz左右时，双层梁—隧道—饱和土体系统刚度减小，对外围土体该点处径向位移幅值的影响才随着频率增加缓慢增大。

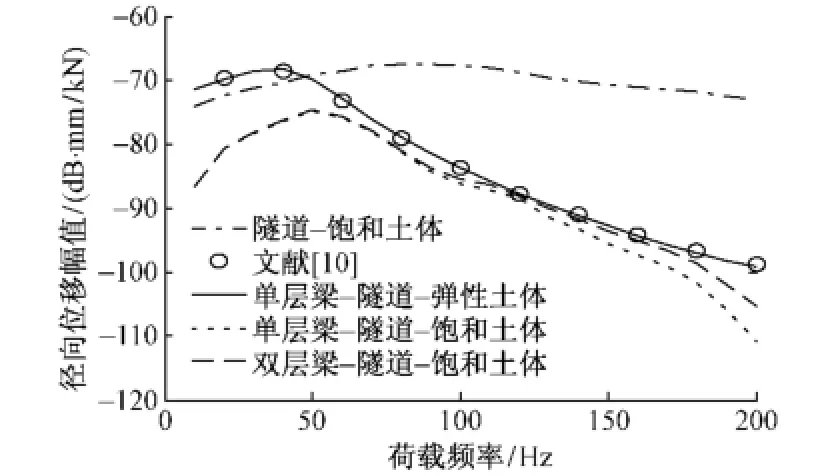
图5 仰拱处径向位移幅值随荷载频率的变化曲线

图6 饱和土体径向位移幅值随荷载频率的变化曲线

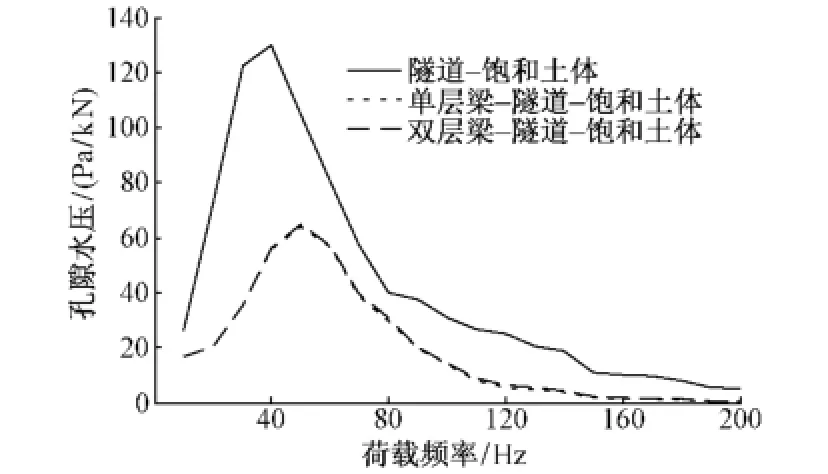
图7 饱和土体孔隙水压幅值随荷载频率的变化曲线

图7表示的是饱和土体中三种隧道系统中r=3.5 m，x=0，θ=0处的孔隙水压幅值变化曲线。隧道—饱和土体系统中该点处的孔隙水压在40 Hz左右达到最大值，而饱和土体中两种浮置板隧道系统该点处孔隙水压在50 Hz左右达到最大值。饱和土体中浮置板隧道对孔隙水压具有明显的减小作用，但双层梁—隧道—饱和土体系统中的上层弹簧、钢轨对外围土体中孔隙水压基本没影响，饱和土体中两种浮置板隧道系统的孔隙水压曲线几乎重合在一起。

图8和图9是饱和土中两种浮置板隧道系统径向、切向位移幅值随环向角度变化曲线。可明显看到，由于荷载非轴对称，两种浮置板隧道系统的位移也不是轴对称分布。在30 Hz的低频荷载作用下，单层梁—隧道—饱和土体和双层梁—隧道—饱和土体系统的径向、切向位移幅值曲线几乎重合在一起，再次说明在低频范围内双层梁—隧道—饱和土体系统中的上层弹簧和钢轨对隧道系统响应的数值及分布的影响基本上都可以忽略。由于土体材料阻尼和辐射阻尼的作用，随着土体与隧道间距离的增加，两种浮置板隧道系统外围饱和土体的径向、切向位移幅值均减小。

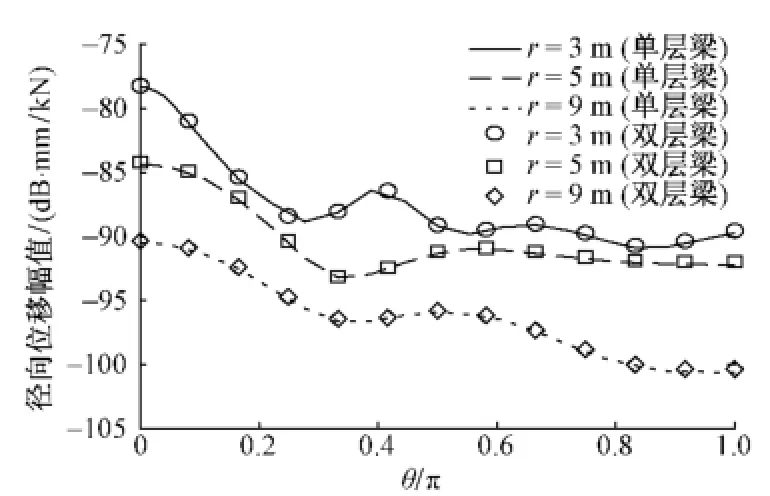
图8 饱和土体中两种浮置板隧道系统径向位移幅值沿环向角度的变化曲线

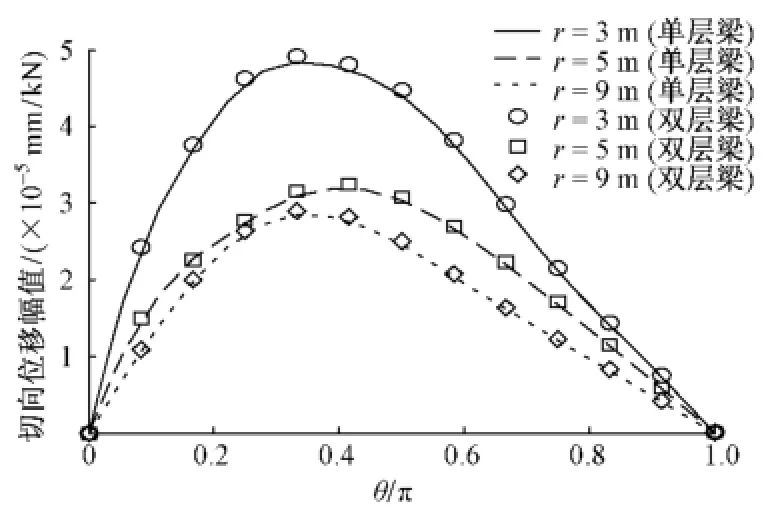
图9 饱和土体中两种浮置板隧道系统切向位移幅值沿环向角度的变化曲线

4 结论

本文将隧道衬砌模拟为薄壁圆柱壳，饱和土体视为Biot理论中的饱和多孔介质，将钢轨、浮置板当成连续支承的无限长Euler梁，根据隧道的连续条件和支承弹簧的受力条件，求得点荷载作用下饱和土中两种浮置板轨道隧道系统的动力响应。从本文的研究中可以得到如下结论:

1)点荷载的频率对饱和土体中两种浮置板轨道隧道系统的动力响应均有较大影响。

2)由于浮置板的影响，饱和土体中两种浮置板隧道系统具有减振作用，特别是在高频范围内，减振作用明显。

3)在低频范围内，双层梁—隧道—饱和土体系统中上层弹簧及Euler梁(钢轨)对浮置板、隧道、外围饱和土体动力响应的影响可以忽略，因此低频荷载作用下可以采用较为简单的单层梁—隧道—饱和土体系统模拟浮置板隧道。

［1］KURZWEIL L G．Ground-borne Noise and Vibrationfrom UndergroundRailSystems［J］．JournalofSoundand Vibration，1979，66(3):363-370．

［2］雷晓燕，王全金，圣小珍．城市轨道交通环境振动与振动噪声研究［J］．铁道学报，2003，25(5):109-113．

［3］NELSON J．Recent Developments in Ground-borne Noise and Vibration Control［J］．Journal of Sound and Vibration，1996，83(1):367-376．

［4］辜小安，任京芳，刘扬，等．我国地铁环境振动现状及控制措施［J］．铁道劳动安全卫生与环保，2003，30(5):1-7．

［5］LOMBAERT G，DEGRANDE G，VANHAUWERE B，et al．The Control of Ground-borne Vibrations from Railway Traffic by Means of Continuous Floating Slabs［J］．Journal of Sound and Vibration，2006，93(3-5):946-961．

［6］CUI F，CHEW C．The Effectiveness of Floating Slab Track System PartⅠ:Receptance Methods［J］．Applied Acoustics，2000(61):441-453．

［7］马龙祥，刘维宁，刘卫丰．移动谐振荷载作用下浮置板轨道的动力响应［J］．工程力学，2012，29(12):334-341．

［8］HUSSEIN M，HUNT H．Modelling of Floating-slab Track with Discontinuous Slab，PartⅡ:Response to Moving Trains［J］．JournalofLowFrequencyNoise，VibrationandActive Control，2006，25(2):111-118．

［9］李增光，吴天行．浮置板轨道二维建模及隔振性能分析［J］．铁道学报，2011，33(8):93-98．

［10］FORREST J，HUNT H．Ground Vibration Generated by Trains in Underground Tunnels［J］．Journal of Sound and Vibration，2006，93(4/5):706-736．

［11］HUSSEIN M，HUNT H．A Numerical for Calculating Vibration from a Railway Tunnel Embedded in a Full-space［J］．Journal of Sound and Vibration，2007，94(3):401-431．

［12］孙成龙，高亮．北京地铁5号线钢弹簧浮置板轨道减振效果测试与分析［J］．铁道建筑，2011(4):110-113．

［13］韦凯，周顺华，翟婉明．地铁—建筑物合建结构中钢弹簧浮置板轨道基频优选影响因素［J］．中国铁道科学，2011，32 (4):8-13．

Study on dynamic response due to harmonic point load to tunnel with floating slab track

HUANG Xiaoji1，2，FU Mingfu1，XU Bin3
(1．School of Civil Engineering Architecture，Nanchang university，Nanchang Jiangxi 330031，China;2．School of Civil Engineering，East China Jiaotong University，Nanchang Jiangxi 330013，China;3．Department of Civil Engineering，Nanchang Institute of Technology，Nanchang Jiangxi 330099，China)

Assuming the tunnel liner as Flügge thin cylindrical shell and the soil as saturated porous medium，the dynamic response of the tunnel-saturated soil system under non-axisymmetrical harmonic point load is calculated by decomposing the load and dynamic response along ring modes circumferentially and using Fourier transformation．On this base，the dynamic response of single beam-tunnel-saturated soil system and double beam-tunnel-saturated soil system under point load is calculated by taking the floating slab and rail as infinite long Euler beam and considering the interaction among the rail，slab，tunnel-saturated soil system．T he research results showed that the load frequency has a great effect on the dynamic response of floating slab tunnel in saturated soil，the floating slab has obvious damping effect，the influence of upper spring and rail in double beam-tunnel-saturated soil system can be ignored in the low frequency range．

Harmonic point load;Floating slab track;T unnel;Saturated soil;Dynamic response

U451+．3

A

10．3969/j．issn．1003-1995．2015．04．39

1003-1995(2015)04-0150-06

(责任审编李付军)

2014-07-26;

2014-09-20

国家自然科学基金(51269021);江西省自然科学基金重点项目(20133ACB20006);江西省教育厅科技项目(GJJ12629，GJJ11253)

黄晓吉(1976—)，女，江西南康人，讲师，博士研究生。